1、基本概念
索引查找又称分级查找。
索引存储的基本思想是:首先把一个集合或线性表(他们对应为主表)按照一定的函数关系或条件划分成若干个逻辑上的子表,为每个子表分别建立一个索引项,由所有
这些索引项构成主表的一个索引表,然后,可采用顺序或链接的方式来存储索引表和每个子表。
索引表的类型可定义如下:
struct IndexItem
{
IndexKeyType index;//IndexKeyType为事先定义的索引值类型
int start; //子表中第一个元素所在的下标位置
int length; //子表的长度域
};
typedef struct IndexItem indexlist[ILMSize];//ILMSize为事先定义的整型常量,大于等于索引项数m主表的类型可定义如下:
typedef struct ElemType mainlist[MaxSize];//MaxSize为事先定义的整型常量,大于等于主表中元素的个数n
在索引表中的每个索引项对应多条记录,则称为稀疏索引,若每个索引项唯一对应一条记录,则称为稠密索引。
2、索引查找算法
过程:
首先根据给定的索引值K1,在索引表上查找出索引值等于K1的索引项,以确定对应子表在主表中的开始位置和长度,然后再根据给定的关键字K2,在对应的子表中查找出
关键字等于K2的元素。
设数组A是具有mainlist类型的一个主表,数组B是具有indexlist类型的在主表A上建立的一个索引表,m为索引表B的实际长度,即所含的索引项的个数,K1和K2分别为给定
带查找的索引值和关键字,并假定每个子表采用顺序存储,则索引查找算法为:
int Indsch(mainlist A, indexlist B, int m, IndexKeyType K1, KeyType K2)
{//利用主表A和大小为 m 的索引表B索引查找索引值为K1,关键字为K2的记录
//返回该记录在主表中的下标位置,若查找失败则返回-1
int i, j;
for (i = 0; i < m; i++)
if (K1 == B[i].index)
break;
if (i == m)
return -1; //查找失败
j = B[i].start;
while (j < B[i].start + B[i].length)
{
if (K2 == A[j].key)
break;
else
j++;
}
if (j < B[i].start + B[i].length)
return j; //查找成功
else
return -1; //查找失败
}
若 IndexKeyType 被定义为字符串类型,则算法中相应的条件改为
strcmp (K1, B[i].index) == 0;
同理,若KeyType 被定义为字符串类型
则算法中相应的条件也应该改为
strcmp (K2, A[j].key) == 0
若每个子表在主表A中采用的是链接存储,则只要把上面算法中的while循环
和其后的if语句进行如下修改即可:
while (j != -1)//用-1作为空指针标记
{
if (K2 == A[j].key)
break;
else
j = A[j].next;
}
return j;
若索引表B为稠密索引,则更为简单,只需查找索引表B,成功时直接返回B[i].start即可。
索引查找分析:
索引查找的比较次数等于算法中查找索引表的比较次数和查找相应子表的比较次数之和,假定索引表的长度为m,子表长度为s,
则索引查找的平均查找长度为:
ASL= (1+m)/2 + (1+s)/2 = 1 + (m+s)/2
假定每个子表具有相同的长度,即s=n/m, 则 ASL = 1 + (m + n/m)/2 ,当m = n/m ,(即m = √▔n,此时s也等于√▔n), ASL = 1 + √▔n 最小 ,时间复杂度为 O(√▔n)
可见,索引查找的速度快于顺序查找,但低于二分查找。
在索引存储中,不仅便于查找单个元素,而且更方便查找一个子表中的全部元素,若在主表中的每个子表后都预留有空闲位置,则索引存储也便于进行插入和删除运算。
3、分块查找
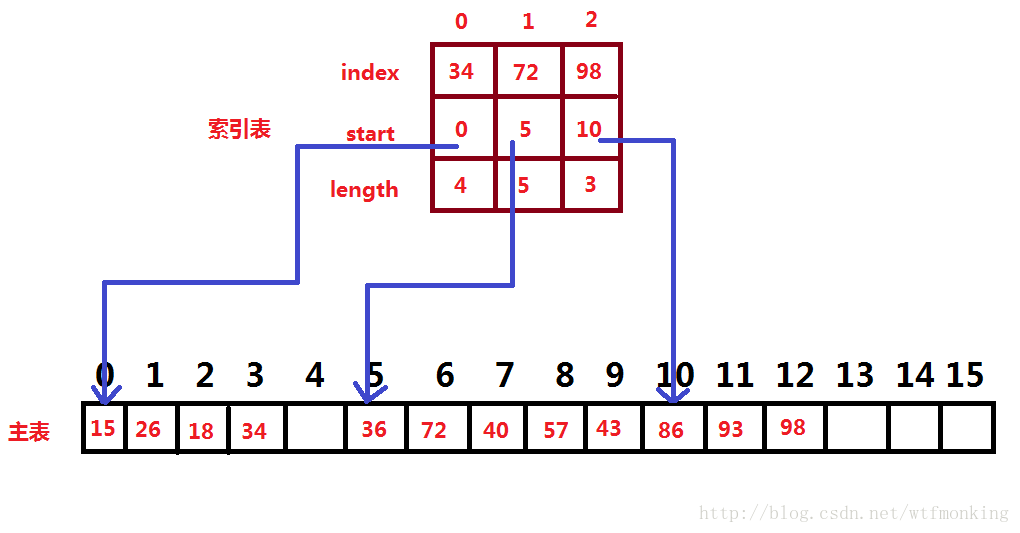
分块查找属于索引查找,其对应的索引表为稀疏索引,具体地说,分块查找要求主表中每个子表(又称为块)之间是递增(或递减)有序的。即前块中最大关键字必须
小于后块中的最小关键字,但块内元素的排列可无序。它还要求索引值域为每块中的最大关键字。
下图是用于分块查找的主表和索引表的示例:
分块查找的算法同上面的索引查找算法类似,具体如下:
int Blocksch(mainlist A, indexlist B, int m, KeyType K)
{//利用主表A和大小为m的索引表B分块查找关键字为K的记录
int i, j;
for (i = 0; i < m; i++)
if (K <= B[i].index)
break;
if (i == m)
return -1; //查找失败
j = B[i].start;
while (j < B[i].start + B[i].length)
{
if (K == A[j].key)
break;
else
j++;
}
if (j < B[i].start + B[i].length)
return j;
else
return -1;
}
若在索引表上不是顺序查找,而是二分查找相应的索引项,则需要把算法中的for循环
语句更换为如下的程序段:
int low = 0, high = m - 1;
while (low <= high)
{
int mid = (low + high) / 2;
if (K == B[mid].index)
{
i = mid;
break;
}
else if (K < B[mid].index)
high = mid - 1;
else
low = mid + 1;
}
if (low > high)
i = low;
这里当二分查找失败时,应把low的值赋给i,此时b[i].index是刚大于K的索引值
当然若low的值为m,则表示真正的查找失败。





















 1240
1240

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








