【剑指offer系列】 二叉搜索树与双向链表___27

　　题目描述：
　　输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。左右孩子指针分别用于双向链表的prev、next指针
　　要求不能创建任何新的节点，只能调整树中节点指针的指向。
　　
　　示例：
　　
　 　　
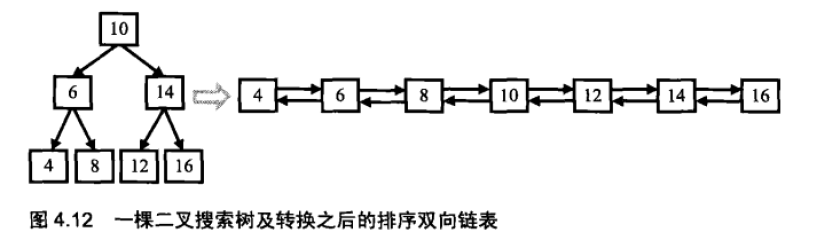
　　分析：
　　由于要求生成的双向链表是排好序的，因此可用中序遍历来遍历这个二叉搜索树。
　　可将二叉搜索树看成三部分：根节点、左、右子树，先分别将左、右子树转换成排序的双向链表之后，再和根节点链接起来
　　　　 　　
　　代码：　 　　

void convert(treeNode *root,treeNode **plast){
    if(root->left)  convert(root->left,plast);   //左子树

    root->left=*plast;             //根节点
    if((*plast)!=NULL){
        (*plast)->right=root;
    }
    *plast=root; 

    if(root->right) convert(root->right,plast);  //右子树
}

treeNode *convertTree(treeNode *root){
    if(root==NULL)  return NULL;

    treeNode *pLast=NULL;
    convert(root,&pLast);
    while(pLast->left){    //向前找到链表头节点
        pLast=pLast->left;
    }
    return pLast;
}

　　相关题目：
　　1、将排序好的单链表转化成BST（leetcode 109）
　　
　　分析：
　　对于BST，根节点为中间值，比根节点小的都在左子树，比根节点大的都在右子树。
　　因此可采用二分法，先递归构建好左子树，再加入根节点，再递归构建好右子树。
　　
　　代码：　　

TreeNode* sortedListToBST(ListNode* head) {
        if(head==NULL)  return NULL;
        ListNode *p=head;
        int len=0;
        while(p){
            p=p->next;
            ++len;   
        }
        return toBST(head,0,len-1);
    }
    TreeNode *toBST(ListNode*& head,int l,int r){       //head is reference
        if(l>r) return NULL;
        int mid=l+(r-l)/2;
        TreeNode *left=toBST(head,l,mid-1);
        TreeNode *root=new TreeNode(head->val);
        root->left=left;
        head=head->next;
        root->right=toBST(head,mid+1,r);
        return root;          //最后一次返回的root恰好是中间节点，即BST的根节点
    }