题目大意
以数集合multiset为背景,求解类似斐波那契数列前n项的和。
解题思路
为了减少时间复杂度,肯定是矩阵快速幂。
先不着急解题,补充一下斐波那契的相关知识。F(n)=F(n-1)+F(n-2)
一.斐波那契数列
斐波那契数列众所周知,F0=0,F1=F2=1,Fn=Fn-1+Fn-2,即数列
1,1,2,3,5,8,13……
矩阵形式:
所以求通项只需要快速幂n次,取结果矩阵第一行第2个元素或第二行第一个元素即可。
这里补充一下矩阵快速幂的相关知识,参考链接:
二.扩展斐波那契数列
扩展的就是更具一般性,F0,F1不一定是0,1;换句话说数列仅仅满足递推公式fn=fn-1+fn-2了,这时候同样有如下矩阵表达式成立:
如果涉及到前n项和Sn,有这样的矩阵表达式:
三.再拓展斐波那契数列
数列满足这样的递推公式:
有等价的矩阵表达式:
看完上面地分析以后,是不是知道该怎么做了?
没错,利用二.拓展斐波那契数列中的关于Sn的矩阵表达式,矩阵快速幂求解就可以得到Sn.
参考代码+部分解释
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <map>
#include <vector>
#include <cstring>
#include<cmath>
#define eps 1e-8
using namespace std;
typedef long long ll;
const int maxn = 1e5+10;
const int mod = 10000007;
ll n,k;
struct matrix
{
ll m[3][3];
}a,p;
matrix multi(matrix a,matrix b)
{
matrix c;
for(int i=0;i<3;i++)
for(int j=0;j<3;j++){
c.m[i][j]=0;
for(int k=0;k<3;k++)
c.m[i][j]+=a.m[i][k]*b.m[k][j];
c.m[i][j]%=mod;
}
return c;
}
matrix quickpow_mod(matrix a,ll b)
{
matrix ans=p;
while(b){
if(b&1) ans=multi(ans,a);
b>>=1;
a=multi(a,a);
}
return ans;
}
int main()
{
// freopen("input.txt","r",stdin);
a.m[0][0]=a.m[0][1]=a.m[0][2]=a.m[1][1]=a.m[1][2]=a.m[2][1]=1;a.m[1][0]=a.m[2][0]=a.m[2][2]=0;//a,p矩阵初始化
p.m[0][0]=p.m[1][1]=p.m[2][2]=1;p.m[1][0]=p.m[0][1]=p.m[0][2]=p.m[1][2]=p.m[2][0]=p.m[2][1]=0;
matrix ans;
int num[maxn];
while(cin>>n>>k){
ll sum=0;
for(int i=0;i<n;i++) {cin>>num[i];sum+=num[i];}sort(num,num+n);//排序找到最大值和第二大值
ll F[3];F[1]=num[n-1]+num[n-2],F[0]=sum+F[1],F[2]=num[n-1];//构建矩阵[S1 F1 F0]',存于F[]数组
ans=quickpow_mod(a,k-1);
ll res=0;
for(int i=0;i<3;i++) res+=ans.m[0][i]*F[i]; res%=mod;
cout<<res<<endl;
}
return 0;
}








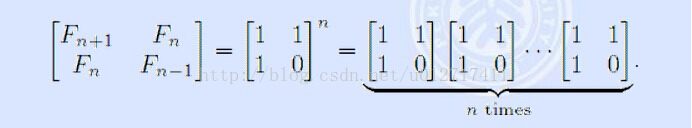
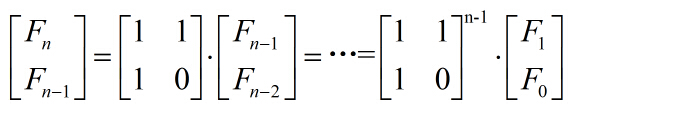
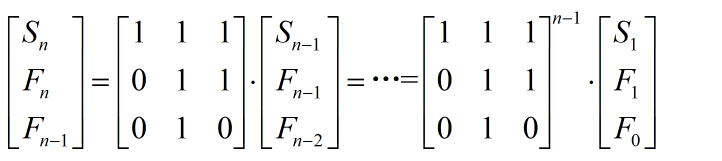
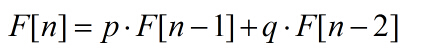
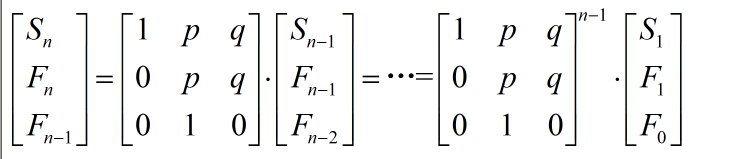














 1494
1494

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








