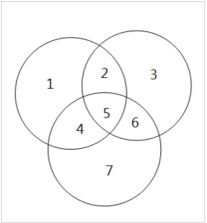
我们尝试从集合论的角度理解容斥
三个圆圈和事件可以表示为
推广到n个集合的容斥关系
可以得到这样的关系:奇数加、偶数减
例题一. poj 3904 Sky Code
题目大意
给一串数字,求解互质四元组的个数(注意不必两两互质)
解题思路
网上有很多代码,但是详细讲解的很少,这里结合笔者的思路详细论述一下解题思路,耐心一看。
首先容易想到,想计算不互质的四元组的个数,再用总的减去,关键是怎样计数不互质四元组的个数??
枚举公约数,对于同一个四元组(6,12,18,36)可能既有公约数2,也有公约数3,和公约数6,我们在枚举过程中是计数到2?3?还是6?
容斥啊!!公约数有奇数个素因子就+,偶数个素因子就-(2、3都含有一个素因子就加,6含有2、3两个素因子就减);找到公约数就要对读入的每一个数据进行素因子分解,对素因子进行组合,记录组合得到因子k含有几个素因子,用num[k]表示;开一个全局数组cnt[k]计数含有因子k的数据个数。然后根据容斥定理,如果因子k含有偶数个素因子(如6=2×3)减,奇数个素因子(如2=2,5=5,30=2×3×5)加,累加起来就得到不互质四元组的总个数啦!
有几个关键点
key 1: 理解cnt[i]表示含有因子i的数据的个数(2,4,6,8,10这组数据中cnt[i]=5)
num[i]表示因子i含有的不同素因子的个数(num[6]=2,减)
key 2:怎样得到cnt[i]、num[i],或者说怎样实现素因子组合?用到了二进制表示的思想,第j位的1表示第j个素因子参与累乘,0表示不参与累乘,比如含有素因子2*3*5*7,1010表示2*1*5*1,0001表示1*1*1*7,以此类推……这样,只要素因子分解完记录含有素因子的个数tol,那么就有tol位二进制,注意到2*3*5*7*11*13>10000,所有最多有6位二进制;对于任意一个范围内的数i,遍历所有位j(从低位到高位),i&(1《《j)==1,表示i的第j位二进制为1,意思是第j个素因子参与累乘;依据这样的意义,遍历二进制范围内的所有数i和i对应的所有二进制数位j,更新数组cnt[k]和num[k]即可!!
key 3:笔者错误的理解了素因子组合不是整数分解得到所有约数,得到了错误的num[i]和cnt[i],举个例子:2,4,8,16,32这组数据,对应的
cnt = 5 , 4 , 3 , 2 , 1
num = 1 , 1 , 1 , 1 , 1
本来不可能有互质四元组的,但在容斥的时候会把cnt[2]、cnt[4]都算进去,原因就在于我进行了约数分解,并不是素因子组合!!!
正确答案是
cnt = 5 , 0 , 0 , 0 , 0
num = 1 , 0 , 0 , 0 , 0 (因为只有一个素因子2无法组合出4,8,16,32)
好了,参考着代码理解一下呗!
参考代码+部分注释
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <map>
#include <vector>
#include <cstring>
#include <cmath>
#include <climits>
#define eps 1e-8
using namespace std;
typedef long long ll;
const int maxx=INT_MAX;
const int maxn = 1e4+10;
int n,m,a[maxn],cnt[maxn],prime[maxn],num[maxn];
ll p[maxn]; //p[i]表示组合数c(i,4)
void init()
{
for(ll i=4;i<maxn;i++) p[i]=i*(i-1)*(i-2)*(i-3)/24;//组合数预处理
return;
}
void divide(int n)
{
int tol=0;
for(int i=2;i*i<=n;i++)
if(n%i==0){
prime[tol++]=i;
do{
n/=i;
}while(n%i==0);
}
if(n>1) prime[tol++]=n; //对n素因子分解,tol表示素因子的个数
for(int i=1;i<(1<<tol);i++){//利用二进制的每一位0、1对素因子进行组合,如:0001~1111
int k=1;
int sum=0;
for(int j=0;j<tol;j++) //从低位到高位遍历,找i在哪一位是1
if(i&(1<<j)){ //与运算,j位为1,执行if语句
k*=prime[j]; //累乘素因子
sum++;
}
cnt[k]++;//cnt[i]表示含有因子i的数据个数
num[k]=sum;//num[i]表示i含有的素因子个数
}
}
int main()
{
// freopen("input.txt","r",stdin);
init();
memset(num,0,sizeof(num));
while(cin>>n){
memset(cnt,0,sizeof(cnt));
for(int i=0;i<n;i++){
cin>>m;
divide(m); //素因子分解,并统计相关数据
}
ll ans=0;
for(int i=2;i<maxn;i++)
if(cnt[i]>=4) {//剪枝,cnt[i]必须大于等于四
if(num[i]&1) ans+=p[cnt[i]];//假如含有素因子个数为奇数,则加上;否则减去
else ans-=p[cnt[i]];
}
cout<<p[n]-ans<<endl; //最后用总的减去不符合的四元组个数
for(int i=2;i<=8;i++) cout<<num[i]<<" ";cout<<endl;
}
return 0;
}









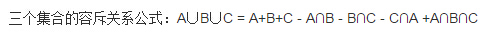
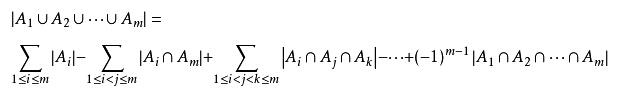















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








