适用场景：整数，无重复；
一. Bitset 基础
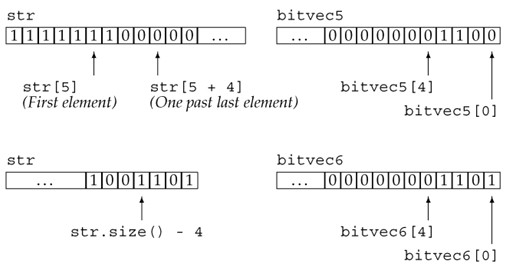
Bitset，也就是位图，由于可以用非常紧凑的格式来表示给定范围的连续数据而经常出现在各种算法设计中。上面的图来自c++库中bitset的一张图。
基本原理是，用1位来表示一个数据是否出现过，0为没有出现过，1表示出现过。使用用的时候既可根据某一个是否为0表示此数是否出现过。
一个1G的空间，有 8*1024*1024*1024=8.58*10^9bit，也就是可以表示85亿个不同的数。
常见的应用是那些需要对海量数据进行一些统计工作的时候，比如日志分析等。
面试题中也常出现，比如：统计40亿个数据中没有出现的数据，将40亿个不同数据进行排序等。
又如：现在有1千万个随机数，随机数的范围在1到1亿之间。现在要求写出一种算法，将1到1亿之间没有在随机数中的数求出来(百度)。
programming pearls上也有一个关于使用bitset来查找电话号码的题目。
Bitmap的常见扩展，是用2位或者更多为来表示此数字的更多信息，比如出现了多少次等。
二. Java中Bitset的实现
Bitset这种结构虽然简单，实现的时候也有一些细节需要主要。其中的关键是一些位操作，比如如何将指定位进行反转、设置、查询指定位的状态（0或者1）等。
本文，分析一下java中bitset的实现，抛砖引玉，希望给那些需要自己设计位图结构的需要的程序员有所启发。
Bitmap的基本操作有：
- 初始化一个bitset，指定大小。
- 清空bitset。
- 反转某一指定位。
- 设置某一指定位。
- 获取某一位的状态。
- 当前bitset的bit总位数。
1. 声明
在java中，bitset的实现，位于java.util这个包中，从jdk 1.0就引入了这个数据结构。在多个jdk的演变中，bitset也不断演变。本文参照的是jdk 7.0 源代码中的实现。
声明如下：
package java.util;
import java.io.*;
import java.nio.ByteBuffer;
import java.nio.ByteOrder;
import java.nio.LongBuffer;
public class BitSet implements Cloneable, java.io.Serializable {、 private long[] words; 2. 初始化函数
<pre name="code" class="java"> public BitSet() {
initWords(BITS_PER_WORD);
sizeIsSticky = false;
}
public BitSet(int nbits) {
// nbits can't be negative; size 0 is OK
if (nbits < 0)
throw new NegativeArraySizeException("nbits < 0: " + nbits);
initWords(nbits);
private void initWords(int nbits) {
words = new long[wordIndex(nbits-1) + 1];
}
private static int wordIndex(int bitIndex) {
return bitIndex >> ADDRESS_BITS_PER_WORD;
}
private final static int ADDRESS_BITS_PER_WORD = 6;
private final static int BITS_PER_WORD = 1 << ADDRESS_BITS_PER_WORD;</pre><br>
两个构造函数，分别是一个指定了初始大小，一个没指定。如果没指定，我们可以看到默认的初始大小为, 2^6 = 64-1=63 bit. 我们知道java中long的大小就是8个字节，也就是8*8=64bit。也就是说，bitset默认的是一个long整形的大小。初始化函数指定了必要的大小。<br>
<strong>注意：</strong>如果指定了bitset的初始化大小，那么会把他规整到一个大于或者等于这个数字的64的整倍数。比如64位，bitset的大小是1个long，而65位时，bitset大小是2个long，即128位。做这么一个规定，主要是为了内存对齐，同时避免考虑到不要处理特殊情况，简化程序。
<pre></pre>
<pre></pre>
<pre></pre>
<pre></pre>3. 清空BitSet
a. 清空所有的bit位，即全部置0。通过循环方式来以此以此置0。 如果是c语言，使用memset会不会快点？
public void clear() {
while (wordsInUse > 0)
words[--wordsInUse] = 0;
}
public void clear(int bitIndex) {
if (bitIndex < 0)
throw new IndexOutOfBoundsException("bitIndex < 0: " + bitIndex);
int wordIndex = wordIndex(bitIndex);
if (wordIndex >= wordsInUse)
return;
words[wordIndex] &= ~(1L << bitIndex);
recalculateWordsInUse();
checkInvariants();
}
第一行是参数检查，如果bitIndex小于0，则抛参数非法异常。后面执行的是bitset中操作中经典的两步曲：a. 找到对应的long b. 操作对应的位。
a. 找到对应的long。 这行语句是 int wordIndex = wordIndex(bitIndex);
b. 操作对应的位。常见的位操作是通过与特定的mask进行逻辑运算来实现的。因此，首先获取 mask（掩码）。
对于 clear某一位来说，它需要的掩码是指定位为0，其余位为1，然后与对应的long进行&运算。
~(1L << bitIndex); 即获取mask
words[wordIndex] &= ; 执行相应的运算。
注意：这里的参数检查，对负数index跑出异常，对超出大小的index，不做任何操作，直接返回。具体的原因，有待进一步思考。
a. 找到对应的long。 这行语句是 int wordIndex = wordIndex(bitIndex);
b. 操作对应的位。常见的位操作是通过与特定的mask进行逻辑运算来实现的。因此，首先获取 mask（掩码）。
对于 clear某一位来说，它需要的掩码是指定位为0，其余位为1，然后与对应的long进行&运算。
~(1L << bitIndex); 即获取mask
words[wordIndex] &= ; 执行相应的运算。
注意：这里的参数检查，对负数index跑出异常，对超出大小的index，不做任何操作，直接返回。具体的原因，有待进一步思考。
c. 清空指定范围的那些bits
/**
* Sets the bits from the specified {@code fromIndex} (inclusive) to the
* specified {@code toIndex} (exclusive) to {@code false}.
*
* @param fromIndex index of the first bit to be cleared
* @param toIndex index after the last bit to be cleared
* @throws IndexOutOfBoundsException if {@code fromIndex} is negative,
* or {@code toIndex} is negative, or {@code fromIndex} is
* larger than {@code toIndex}
* @since 1.4
*/
public void clear(int fromIndex, int toIndex) {
checkRange(fromIndex, toIndex);
if (fromIndex == toIndex)
return;
int startWordIndex = wordIndex(fromIndex);
if (startWordIndex >= wordsInUse)
return;
int endWordIndex = wordIndex(toIndex - 1);
if (endWordIndex >= wordsInUse) {
toIndex = length();
endWordIndex = wordsInUse - 1;
}
long firstWordMask = WORD_MASK << fromIndex;
long lastWordMask = WORD_MASK >>> -toIndex;
if (startWordIndex == endWordIndex) {
// Case 1: One word
words[startWordIndex] &= ~(firstWordMask & lastWordMask);
} else {
// Case 2: Multiple words
// Handle first word
words[startWordIndex] &= ~firstWordMask;
// Handle intermediate words, if any
for (int i = startWordIndex+1; i < endWordIndex; i++)
words[i] = 0;
// Handle last word
words[endWordIndex] &= ~lastWordMask;
}
recalculateWordsInUse();
checkInvariants();
}其中startword，只要将从start位到该word结束位全部置0；interval words则是这些long的所有bits全部置0；而stopword这是从起始位置到指定的结束位全部置0。
而特殊情形则是没有startword和stopword是同一个long。
具体的实现，参照代码，是分别作出两个mask，对startword和stopword进行操作。
4. 重要的两个内部检查函数
从上面的代码，可以看到每个函授结尾都会有两个函数,如下：recalculateWordsInUse();
checkInvariants();
这两个函数，是对bitset的内部状态进行维护和检查的函数。细看实现既可明白其中原理：
/**
* Sets the field wordsInUse to the logical size in words of the bit set.
* WARNING:This method assumes that the number of words actually in use is
* less than or equal to the current value of wordsInUse!
*/
private void recalculateWordsInUse() {
// Traverse the bitset until a used word is found
int i;
for (i = wordsInUse-1; i >= 0; i--)
if (words[i] != 0)
break;
wordsInUse = i+1; // The new logical size
}
/**
* Every public method must preserve these invariants.
*/
private void checkInvariants() {
assert(wordsInUse == 0 || words[wordsInUse - 1] != 0);
assert(wordsInUse >= 0 && wordsInUse <= words.length);
assert(wordsInUse == words.length || words[wordsInUse] == 0);
} 5. 反转某一个指定位
反转，就是1变成0,0变成1，是一个与1的xor操作。
/**
* Sets the bit at the specified index to the complement of its
* current value.
*
* @param bitIndex the index of the bit to flip
* @throws IndexOutOfBoundsException if the specified index is negative
* @since 1.4
*/
public void flip(int bitIndex) {
if (bitIndex < 0)
throw new IndexOutOfBoundsException("bitIndex < 0: " + bitIndex);
int wordIndex = wordIndex(bitIndex);
expandTo(wordIndex);
words[wordIndex] ^= (1L << bitIndex);
recalculateWordsInUse();
checkInvariants();
}
int wordIndex = wordIndex(bitIndex);
words[wordIndex] ^= (1L << bitIndex);
我们注意到在进行操作之前，执行了一个函数 expandTo(wordIndex); 这个函数是确保bitset中有对应的这个long。如果没有的话，就对bitset中的long数组进行扩展。扩展的策略，是将当前的空间翻一倍。
代码如下：
/**
* Ensures that the BitSet can accommodate a given wordIndex,
* temporarily violating the invariants. The caller must
* restore the invariants before returning to the user,
* possibly using recalculateWordsInUse().
* @param wordIndex the index to be accommodated.
*/
private void expandTo(int wordIndex) {
int wordsRequired = wordIndex+1;
if (wordsInUse < wordsRequired) {
ensureCapacity(wordsRequired);
wordsInUse = wordsRequired;
}
}
/**
* Ensures that the BitSet can hold enough words.
* @param wordsRequired the minimum acceptable number of words.
*/
private void ensureCapacity(int wordsRequired) {
if (words.length < wordsRequired) {
// Allocate larger of doubled size or required size
int request = Math.max(2 * words.length, wordsRequired);
words = Arrays.copyOf(words, request);
sizeIsSticky = false;
}
}
public void flip(int fromIndex, int toIndex) {
checkRange(fromIndex, toIndex);
if (fromIndex == toIndex)
return;
int startWordIndex = wordIndex(fromIndex);
int endWordIndex = wordIndex(toIndex - 1);
expandTo(endWordIndex);
long firstWordMask = WORD_MASK << fromIndex;
long lastWordMask = WORD_MASK >>> -toIndex;
if (startWordIndex == endWordIndex) {
// Case 1: One word
words[startWordIndex] ^= (firstWordMask & lastWordMask);
} else {
// Case 2: Multiple words
// Handle first word
words[startWordIndex] ^= firstWordMask;
// Handle intermediate words, if any
for (int i = startWordIndex+1; i < endWordIndex; i++)
words[i] ^= WORD_MASK;
// Handle last word
words[endWordIndex] ^= lastWordMask;
}
recalculateWordsInUse();
checkInvariants();
}
6. 设置某一指定位 （or 操作）
/**
* Sets the bit at the specified index to {@code true}.
*
* @param bitIndex a bit index
* @throws IndexOutOfBoundsException if the specified index is negative
* @since JDK1.0
*/
public void set(int bitIndex) {
if (bitIndex < 0)
throw new IndexOutOfBoundsException("bitIndex < 0: " + bitIndex);
int wordIndex = wordIndex(bitIndex);
expandTo(wordIndex);
words[wordIndex] |= (1L << bitIndex); // Restores invariants
checkInvariants();
} 同时jdk中提供了，具体设置成0或1的操作，以及设置某一区间的操作。
public void set(int bitIndex, boolean value) {
if (value)
set(bitIndex);
else
clear(bitIndex);
} 7. 获取某一位置的状态
/**
* Returns the value of the bit with the specified index. The value
* is {@code true} if the bit with the index {@code bitIndex}
* is currently set in this {@code BitSet}; otherwise, the result
* is {@code false}.
*
* @param bitIndex the bit index
* @return the value of the bit with the specified index
* @throws IndexOutOfBoundsException if the specified index is negative
*/
public boolean get(int bitIndex) {
if (bitIndex < 0)
throw new IndexOutOfBoundsException("bitIndex < 0: " + bitIndex);
checkInvariants();
int wordIndex = wordIndex(bitIndex);
return (wordIndex < wordsInUse)
&& ((words[wordIndex] & (1L << bitIndex)) != 0);
} jdk同时提供了一个获取指定区间的bitset的方法。当然这里的返回值会是一个bitset，是一个仅仅包含需要查询位的bitset。注意这里的大小也仅仅是刚刚能够容纳必须的位（当然，规整到long的整数倍）。代码如下：
public BitSet get(int fromIndex, int toIndex) {
checkRange(fromIndex, toIndex);
checkInvariants();
int len = length();
// If no set bits in range return empty bitset
if (len <= fromIndex || fromIndex == toIndex)
return new BitSet(0);
// An optimization
if (toIndex > len)
toIndex = len;
BitSet result = new BitSet(toIndex - fromIndex);
int targetWords = wordIndex(toIndex - fromIndex - 1) + 1;
int sourceIndex = wordIndex(fromIndex);
boolean wordAligned = ((fromIndex & BIT_INDEX_MASK) == 0);
// Process all words but the last word
for (int i = 0; i < targetWords - 1; i++, sourceIndex++)
result.words[i] = wordAligned ? words[sourceIndex] :
(words[sourceIndex] >>> fromIndex) |
(words[sourceIndex+1] << -fromIndex);
// Process the last word
long lastWordMask = WORD_MASK >>> -toIndex;
result.words[targetWords - 1] =
((toIndex-1) & BIT_INDEX_MASK) < (fromIndex & BIT_INDEX_MASK)
? /* straddles source words */
((words[sourceIndex] >>> fromIndex) |
(words[sourceIndex+1] & lastWordMask) << -fromIndex)
:
((words[sourceIndex] & lastWordMask) >>> fromIndex);
// Set wordsInUse correctly
result.wordsInUse = targetWords;
result.recalculateWordsInUse();
result.checkInvariants();
return result;
}其中>>>是无符号位想右边移位的操作符。
8. 获取当前bitset总bit的大小
/**
* Returns the "logical size" of this {@code BitSet}: the index of
* the highest set bit in the {@code BitSet} plus one. Returns zero
* if the {@code BitSet} contains no set bits.
*
* @return the logical size of this {@code BitSet}
* @since 1.2
*/
public int length() {
if (wordsInUse == 0)
return 0;
return BITS_PER_WORD * (wordsInUse - 1) +
(BITS_PER_WORD - Long.numberOfLeadingZeros(words[wordsInUse - 1]));
}9. hashcode
hashcode是一个非常重要的属性，可以用来表明一个数据结构的特征。bitset的hashcode是用下面的方式实现的：/**
* Returns the hash code value for this bit set. The hash code depends
* Note that the hash code changes if the set of bits is altered.
*
* @return the hash code value for this bit set
*/
public int hashCode() {
long h = 1234;
for (int i = wordsInUse; --i >= 0; )
h ^= words[i] * (i + 1);
return (int)((h >> 32) ^ h);
}
这个hashcode同时考虑了没给word以及word的位置。当有bit的状态发生变化时，hashcode会随之改变。
三. Java中Bitset的使用
转载自：http://blog.csdn.net/cpfeed/article/details/7342480
BitSet简介
类实现了一个按需增长的位向量。位 set 的每个组件都有一个boolean值。用非负的整数将BitSet的位编入索引。可以对每个编入索引的位进行测试、设置或者清除。通过逻辑与、逻辑或和逻辑异或操作，可以使用一个BitSet修改另一个BitSet的内容。
默认情况下，set 中所有位的初始值都是false。
每个位 set 都有一个当前大小，也就是该位 set 当前所用空间的位数。注意，这个大小与位 set 的实现有关，所以它可能随实现的不同而更改。位 set 的长度与位 set 的逻辑长度有关，并且是与实现无关而定义的。
除非另行说明，否则将 null 参数传递给BitSet中的任何方法都将导致NullPointerException。
在没有外部同步的情况下，多个线程操作一个BitSet是不安全的
基本原理
BitSet是位操作的对象，值只有0或1即false和true，内部维护了一个long数组，初始只有一个long，所以BitSet最小的size是64，当随着存储的元素越来越多，BitSet内部会动态扩充，最终内部是由N个long来存储，这些针对操作都是透明的。
用1位来表示一个数据是否出现过，0为没有出现过，1表示出现过。使用用的时候既可根据某一个是否为0表示，此数是否出现过。
一个1G的空间，有 8*1024*1024*1024=8.58*10^9bit，也就是可以表示85亿个不同的数
使用场景
常见的应用是那些需要对海量数据进行一些统计工作的时候，比如日志分析、用户数统计等等
如统计40亿个数据中没有出现的数据，将40亿个不同数据进行排序等。
现在有1千万个随机数，随机数的范围在1到1亿之间。现在要求写出一种算法，将1到1亿之间没有在随机数中的数求出来
代码示例
package util;
import java.util.Arrays;
import java.util.BitSet;
public class BitSetDemo {
/**
* 求一个字符串包含的char
*
*/
public static void containChars(String str) {
BitSet used = new BitSet();
for (int i = 0; i < str.length(); i++)
used.set(str.charAt(i)); // set bit for char
StringBuilder sb = new StringBuilder();
sb.append("[");
int size = used.size();
System.out.println(size);
for (int i = 0; i < size; i++) {
if (used.get(i)) {
sb.append((char) i);
}
}
sb.append("]");
System.out.println(sb.toString());
}
/**
* 求素数 有无限个。一个大于1的自然数，如果除了1和它本身外，不能被其他自然数整除(除0以外）的数称之为素数(质数） 否则称为合数
*/
public static void computePrime() {
BitSet sieve = new BitSet(1024);
int size = sieve.size();
for (int i = 2; i < size; i++)
sieve.set(i);
int finalBit = (int) Math.sqrt(sieve.size());
for (int i = 2; i < finalBit; i++)
if (sieve.get(i))
for (int j = 2 * i; j < size; j += i)
sieve.clear(j);
int counter = 0;
for (int i = 1; i < size; i++) {
if (sieve.get(i)) {
System.out.printf("%5d", i);
if (++counter % 15 == 0)
System.out.println();
}
}
System.out.println();
}
/**
* 进行数字排序
*/
public static void sortArray() {
int[] array = new int[] { 423, 700, 9999, 2323, 356, 6400, 1,2,3,2,2,2,2 };
BitSet bitSet = new BitSet(2 << 13);
// 虽然可以自动扩容，但尽量在构造时指定估算大小,默认为64
System.out.println("BitSet size: " + bitSet.size());
for (int i = 0; i < array.length; i++) {
bitSet.set(array[i]);
}
//剔除重复数字后的元素个数
int bitLen=bitSet.cardinality();
//进行排序，即把bit为true的元素复制到另一个数组
int[] orderedArray = new int[bitLen];
int k = 0;
for (int i = bitSet.nextSetBit(0); i >= 0; i = bitSet.nextSetBit(i + 1)) {
orderedArray[k++] = i;
}
System.out.println("After ordering: ");
for (int i = 0; i < bitLen; i++) {
System.out.print(orderedArray[i] + "\t");
}
System.out.println("iterate over the true bits in a BitSet");
//或直接迭代BitSet中bit为true的元素iterate over the true bits in a BitSet
for (int i = bitSet.nextSetBit(0); i >= 0; i = bitSet.nextSetBit(i + 1)) {
System.out.print(i+"\t");
}
System.out.println("---------------------------");
}
/**
* 将BitSet对象转化为ByteArray
* @param bitSet
* @return
*/
public static byte[] bitSet2ByteArray(BitSet bitSet) {
byte[] bytes = new byte[bitSet.size() / 8];
for (int i = 0; i < bitSet.size(); i++) {
int index = i / 8;
int offset = 7 - i % 8;
bytes[index] |= (bitSet.get(i) ? 1 : 0) << offset;
}
return bytes;
}
/**
* 将ByteArray对象转化为BitSet
* @param bytes
* @return
*/
public static BitSet byteArray2BitSet(byte[] bytes) {
BitSet bitSet = new BitSet(bytes.length * 8);
int index = 0;
for (int i = 0; i < bytes.length; i++) {
for (int j = 7; j >= 0; j--) {
bitSet.set(index++, (bytes[i] & (1 << j)) >> j == 1 ? true
: false);
}
}
return bitSet;
}
/**
* 简单使用示例
*/
public static void simpleExample() {
String names[] = { "Java", "Source", "and", "Support" };
BitSet bits = new BitSet();
for (int i = 0, n = names.length; i < n; i++) {
if ((names[i].length() % 2) == 0) {
bits.set(i);
}
}
System.out.println(bits);
System.out.println("Size : " + bits.size());
System.out.println("Length: " + bits.length());
for (int i = 0, n = names.length; i < n; i++) {
if (!bits.get(i)) {
System.out.println(names[i] + " is odd");
}
}
BitSet bites = new BitSet();
bites.set(0);
bites.set(1);
bites.set(2);
bites.set(3);
bites.andNot(bits);
System.out.println(bites);
}
public static void main(String args[]) {
//BitSet使用示例
BitSetDemo.containChars("How do you do? 你好呀");
BitSetDemo.computePrime();
BitSetDemo.sortArray();
BitSetDemo.simpleExample();
//BitSet与Byte数组互转示例
BitSet bitSet = new BitSet();
bitSet.set(3, true);
bitSet.set(98, true);
System.out.println(bitSet.size()+","+bitSet.cardinality());
//将BitSet对象转成byte数组
byte[] bytes = BitSetDemo.bitSet2ByteArray(bitSet);
System.out.println(Arrays.toString(bytes));
//在将byte数组转回来
bitSet = BitSetDemo.byteArray2BitSet(bytes);
System.out.println(bitSet.size()+","+bitSet.cardinality());
System.out.println(bitSet.get(3));
System.out.println(bitSet.get(98));
for (int i = bitSet.nextSetBit(0); i >= 0; i = bitSet.nextSetBit(i + 1)) {
System.out.print(i+"\t");
}
}
}转载自：https://my.oschina.net/cloudcoder/blog/294810
扫一扫
570
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
