计数排序

转载于：http://blog.csdn.net/llzk_/article/details/53354071

排序总归来说可分为两大类，比较排序与非比较排序。比较排序就是我们常用到的冒泡排序，插入排序，希尔排序，选择排序，堆排序，快速排序，归并排序。非比较排序不常用，但是在对一些特殊的情况进行处理时，它的速度反而更快。

1、计数排序  

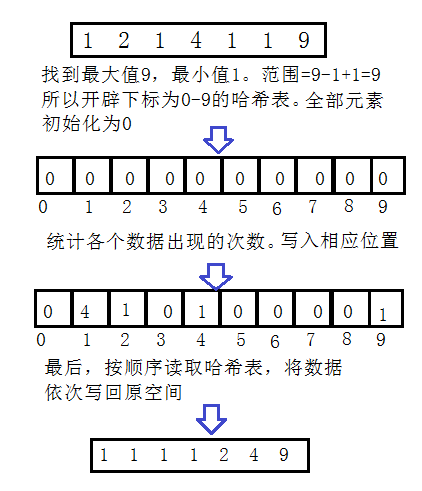
排序原理：利用哈希的方法，将每个数据出现的次数都统计下来。哈希表是顺序的，所以我们统计完后直接遍历哈希表，将数据再重写回原数据空间就可以完成排序。

注意事项：

①因为要建立哈希表，计数排序只适用于对数据范围比较集中的数据集合进行排序。范围分散情况太浪费空间。如我有100个数，其中前99个都小于100，最后一个数位是10000，我们总不能开辟10000个数据大小的哈希表来进行排序吧！这样空间就太浪费了。 此时，就得考虑其他的算法了。当然，这个例子也可能不恰当，这里只是想让你们直观的理解。
②除了上面那种情况，还有一个问题，例如我有一千个数，1001~2000，此时我的哈希表该怎么开辟呢？ 开0~2000个？那前面1000个空间就浪费了！直接从1001开始开辟？你想多了！所以这种情况我们就需要遍历一遍数据，找出最大值与最小值，求出数据范围。范围 = 最大值 - 最小值+1。 例如，2000-1001+1 = 1000，这样我们就开辟0~1000个空间，用1代表1001,1000代表2000。节省了大量的空间。

③肯定有同学想到用位图（BitMap）来做，但是位图（BitMap）有局限性，它要求每个数据只能出现一次。算法有些复杂，但是可以尝试。

时间复杂度分析：综上所述，我们总需要两遍遍历，第一遍统计字数据出现次数，遍历原数据，复杂度为O(N)，第二遍遍历哈希表，向原空间写数据,遍历了范围次（range），时间复杂度为O(range)，所以总的时间复杂度为O(N+range)。

空间复杂度分析：开辟了范围（range）大小的辅助哈希表，所以空间复杂度为O(range)。

下面我对一组数据进行排序做出图解：

缺点：这个算法的简洁性同时也是它的弱点。很多程序员不需要对整数排序。其实通常非整数都可以被规约为整数，然后再用计数排序或者基数排序。

c++代码实现：

[cpp]  view plain  copy

1. void CountSort(int *a, int n)  
2. {  
3.     assert(a);  
4.   
5.     int max = a[0];  
6.     int min = a[0];  
7.     //选出最大数与最小数，确定哈希表的大小  
8.     for (int i = 0; i < n; ++i)  
9.     {  
10.         if (a[i] > max)  
11.         {  
12.             max = a[i];  
13.         }  
14.         if (a[i] < min)  
15.         {  
16.             min = a[i];  
17.         }  
18.     }  
19.   
20.     int range = max - min + 1;  
21.     int *count = new int[range];  
22.     memset(count, 0, sizeof(int)*range);//当初始化成0或-1的时候可以用memset，其他情况均用for循环  
23.     /*for (int i = 0; i < range; ++i) 
24.     { 
25.         count[i] = 0; 
26.     }*/  
27.     for (int i = 0; i < n; ++i)  
28.     {  
29.         count[a[i] - min]++;  
30.     }  
31.     //将数据重新写回数组  
32.     int j = 0;  
33.     for (int i = 0; i < range; ++i)  
34.     {  
35.           
36.         while ((count[i]--) > 0)  
37.         {  
38.             a[j] = i + min;  
39.             j++;  
40.         }  
41.     }  
42. }