2.1几何基本元素和变换 36
2.1.1 2D变换 40
2.1.2三维变换 43
2.1.3 3D旋转 45
2.1.4 3D到2D投影 51
2.1.5镜头畸变 63
2.2光度图像形成 66
2.2.1照明 66
2.2.2反射率和阴影 67
2.2.3光学 74
2.3数码相机 79
2.3.1取样和混叠 84
2.3.2颜色 87
2.3.3压缩 98
2.4其他阅读材料 101
2.5练习 102

在我们能够分析和处理图像之前,需要建立一套词汇来描述场景的几何特征。同时,还需要理解在特定光照条件、场景几何形状、表面属性和相机光学条件下生成特定图像的过程。本章中,我们将介绍这一图像生成过程的简化模型。
第2.1节介绍了全书使用的几何基本元素(点、线和平面)以及将这些三维量投影到二维图像特征中的几何变换(图2.1a)。第2.2节描述了光照、表面属性(图2.1b)和相机光学(图2.1c)如何相互作用,产生落在图像传感器上的颜色值。第2.3节描述了连续彩色图像如何在图像传感器内转换为离散数字样本(图2.1d),以及如何避免(或至少识别)采样缺陷,如混叠。
本章所涵盖的内容只是众多独立领域中丰富而深入主题的简要概述。关于点、线、面和投影几何的更全面介绍,可以在多视图几何(哈特利和齐瑟曼2004;福加拉斯和隆2001)和计算机图形学(休斯、范达姆等人2013)的教科书中找到。图像形成(合成)过程传统上作为计算机图形学课程的一部分进行教学(格拉斯纳1995;瓦特1995;休斯、范达姆等人2013;马尔施纳和雪莉2015),但也在基于物理的计算机视觉研究中探讨(沃尔夫、沙弗和希利1992a)。相机镜头系统的特性在光学中被研究(莫勒1988;雷1902;赫克特2015)。一些优秀的色彩理论书籍包括希利和沙弗(1992)、万德尔(1995)以及维泽基和斯蒂尔斯(2000),而利文斯顿(2008)则提供了一个更加有趣且非正式的色彩感知入门。与采样和混叠相关的话题则在信号和图像处理教科书中有所涉及(克兰1997;雅各布森1997;奥本海姆和沙弗1996;奥本海姆、沙弗和巴克1999;普拉特2007;拉塞尔2007;伯格和伯奇2008;冈萨雷斯和伍兹2017)。最近由池内、松下等人(2020)撰写的书籍也涵盖了三维几何、光度学和传感器模型,重点放在主动照明系统上。
给学生的提示:如果你已经学习过计算机图形学,可以略读第2.1节的内容,尽管第2.1.4节末尾关于投影深度和以物体为中心的投影的部分可能对你来说是新的。同样,物理系学生(以及计算机图形学学生)大多会对第2.2节的内容熟悉。最后,具有良好图像处理背景的学生已经熟悉采样问题。
在本节中,我们将介绍本教材中使用的二维和三维基本元素,即点、线和平面。我们还将描述三维特征如何投影到二维特征上。关于这些主题的更详细描述(以及更加温和直观的介绍)可以在多视图几何教科书中找到(Hartley和Zisserman 2004;Faugeras和Luong 2001)。
几何基本元素构成了描述三维形状的基本构建块。在本节中,我们将介绍点、线和面。本书后续章节将讨论曲线(第7.3节和第12.2节)、曲面(第13.3节)以及体积(第13.5节)。
二维点。二维点(图像中的像素坐标)可以用一对值表示,x =(x,y)∈R2,或

(如引言中所述,我们使用(x1,x2,.. .)符号表示列向量。)
二维点也可以用齐次坐标表示,∈P2,其中只相差比例的向量被视为
其中,x- = (x,y,1)是增广向量。=0称为理想
点或无穷远点,没有等价的非齐次表示。
~
二维直线。二维直线也可以用齐次坐标l =(a,b,c)表示。相应的直线方程为
x- · = ax + by + c = 0. (2.3)
我们可以使直线方程向量l =(x,y,d)=(,d)归一化,其中Ⅱ = 1。
在这个例子中,n是垂直于直线的法向量,d是它到原点的距离
(图2.2)。(唯一的例外是无穷线= (0,0,1),
包括所有(理想)无穷点。)

图2.2 (a) 2D直线方程和(b) 3D平面方程,以如下方式表示
正常值和到原点的距离d。
我们也可以表示为旋转角度θ的函数,=(x,y)==(cosθ,sinθ)(图2.2a)。这种表示方法常用于霍夫变换中的直线寻找算法,相关内容将在第7.4.2节讨论。组合(θ,d)也被称为极坐标。
= 1 × 2 , (2.4)
其中×是叉积运算符。同样地,连接两点的直线可以表示为
= 1
× 2 . (2.5)
当试图将一个交点拟合到多条线或相反地,将一条线拟合到多个点时,可以使用最小二乘法技术(第8.1.1节和附录A.2),如练习2.1中所讨论的。
二维圆锥曲线。还有其他代数曲线可以用简单的多项式齐次方程来表示。例如,圆锥曲线(之所以这样称呼是因为它们是平面与三维圆锥相交产生的)可以用二次方程来表示
T
Q~x = 0. (2.6)
二次方程在多视图几何和相机校准研究中发挥着重要作用(Hartley和Zisserman2004;Faugeras和Luong2001),但本书并未广泛使用二次方程。
三维点。可以用非齐次坐标x =(x,y,z)∈R3,,,∈P3来表示三维点的坐标。和之前一样,

有时用增广向量x- = (x,y,z,1)表示一个三维点是有用的
三维平面,带相应
- · = ax + by + cz + d = 0. (2.7)
我们也可以将平面方程规范化为m =(x,y,z,d)=(,d),其中Ⅱ Ⅱ = 1。
在这种情况下,法向量垂直于平面,d是它到原点的距离(图2.2b)。与二维直线的情况类似,包含所有无穷远点的=(0,0,0,1)无法归一化(即
,它没有唯一的法向量或有限距离)。
=(cos θ cos φ,sin θ cos φ,sin φ), (2.8)
即,使用球面坐标系,但是这些坐标系的使用频率低于极坐标系,因为它们不能均匀地采样可能的法向量空间。
三维线。三维线不如二维线或三维平面那么优雅。一种可能的表示方法是使用线上的两个点,(p,q)。线上的任何其他点都可以用这两个点的线性组合来表示
r = (1 — λ)p + λq, (2.9)
如图2.3所示,如果我们将0≤λ≤1限制起来,我们得到连接p和q的线段。如果我们使用齐次坐标,我们可以将这条直线写为
~r =
当第二个点位于无穷远时,即x、y、z、0) = (,0),这是一个特殊
情况。这里,我们看到的是直线的方向。然后,我们可以将非齐次三维直线方程重写为
r = p + λ . (2.11)
三维线的端点表示的一个缺点是它具有过多的自由度,即六个(每个端点三个),而不是三维线真正拥有的四个自由度。然而,如果我们固定线上的两个点位于特定平面上,就可以得到一个具有四个自由度的表示。例如,如果我们表示接近垂直的线,则z = 0和z = 1形成了两个合适的平面,也就是说,这两个平面上的(x,y)坐标提供了描述这条线所需的四个坐标。这种双平面参数化方法在第14章中描述的光场和基于光图的图像渲染系统中被用于表示相机在物体前移动时看到的光线集合。端点表示对于表示线段也非常有用,即使它们的确切端点无法直接看到(只能猜测)。
如果我们希望表示所有可能的线而不偏向任何特定的方向,可以使用普莱克坐标(Hartley和Zisserman
2004,第3.2节;Faugeras和Luong 2001,第3章)。这些坐标是4×4斜对称矩阵中的六个独立非零元素。
L = ~p~qT - ~q~pT , (2.12)
线
上的
任意两点(非相同点)。这种表示法只有四个自由度,因为L是齐次的并且也满足j Lj = 0,这导致了对Plcker坐标的二次约束。
在实际应用中,最小表示对于大多数情况并非必不可少。通过估计线的方向(例如,在建筑设计中可能事先已知)和可见部分的一个点(见第11.4.8节),或者使用两个端点,可以获得三维直线的适当模型,因为直线通常以有限线段的形式可见。然而,如果您对最小线参数化的主题更感兴趣,Fo...rstner(2005)讨论了投影几何中推断和建模三维直线的各种方法,以及如何估计这些拟合模型中的不确定性。
三维二次曲面。圆锥曲线的三维类比是二次曲面
x-TQx- = 0 (2.13)
(Hartley和Zisserman2004,第3章)。同样,虽然二次曲面在多视图几何研究中很有用,也可以作为有用的建模原语(球体、椭球体、圆柱体),但我们在本书中没有详细研究它们。
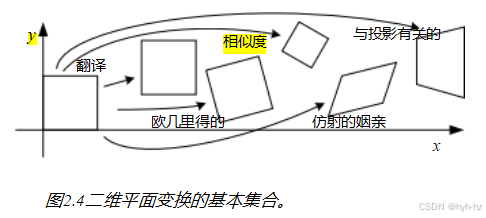
在定义了基本元素之后,现在我们可以考虑如何对它们进行变换。最简单的二维平面变换如图2.4所示。
转换。二维转换可以写成x,= x + t或
其中I是(2×2)单位矩阵或
(2.15)
其中0是零向量。使用2×3矩阵可以得到更简洁的表示,而使用满秩的3×3矩阵(可以通过在2×3矩阵后面添加一行[0T 1]得到)则可以利用矩阵乘法进行变换链式计算以及求逆变换。请注意,在任何包含增广向量的方程中,例如
x- .
旋转+平移。这种变换也被称为二维刚体运动或二维欧几里得变换(因为保持了欧几里得距离)。它可以写成x,= Rx + t或
是一个正交旋转矩阵,其中RRT = I且j Rj = 1。
缩放旋转。也称为相似变换,该变换可以表示为x,= sRx + t,其中s是任意比例因子。它也可以写为
我们不再要求a2 + b2 = 1。相似变换保持线之间的角度。
仿射变换。仿射变换写为x,= Ax-,其中A是任意的2×3矩阵,即
(2.19)
在仿射变换下,平行线保持平行。
投影变换。这种变换也被称为透视变换或单应性变换,它作用于齐次坐标,
= ~x, (2.20)
是一个任意的3×3矩阵。注意,它是齐次的,即它仅在尺度上定义,而且两个仅在尺度上不同的矩阵是等价的。结果
透视变换保留直线(即,变换后保持直线)。
二维变换的层次结构。上述变换集如图2.4所示,并总结于表2.1中。最简单的理解方式是将其视为一组(可能受限的)3×3矩阵,作用于二维齐次坐标向量。Hartley和Zisserman(2004)对二维平面变换的层次结构进行了更详细的描述。
上述变换构成了一组嵌套的群,即它们在组合下是封闭的,并且有一个逆元属于同一群。(这将在第3.6节中将这些变换应用于图像时非常重要。)每个(更简单的)群都是其下方更复杂群的子群。这类李群及其数学性质

表2.1二维坐标变换层次,列出了变换名称、矩阵形式、自由度数、所保留的几何性质以及助记图标。每个变换还保留了其下方行中列出的性质,例如,相似性不仅保持角度,还保持平行性和直线。2×3矩阵通过增加第三行[0T 1]扩展为完整的3×3矩阵,用于齐次坐标变换。
相关的代数(原点处的切空间)在最近的一些机器人教程中有所讨论(Dellaert和Kaess 2017;Blanco 2019;Sol、Deray和Atchuthan 2019),其中二维旋转和刚体变换被称为SO(2)和SE(2),分别代表特殊正交群和特殊欧几里得群。
共向量。虽然上述变换可以用于变换二维平面上的点,但它们是否也可以直接用于变换直线方程?考虑齐次方程
· / = /T~x = (T/ )T
= ·
即,/=—T。因此,射影变换对一个协向量的作用,如二维
线或三维法线可以用矩阵的转置逆来表示,即等价于
对的副手,因为射影变换矩阵是齐次的。吉姆
Blinn(1998)在第9章和第10章中描述了表示和操作共向量的细节。
虽然上述转换是我们最常用的,但有时也会使用一些其他转换。
拉伸/压扁。此转换会更改图像的纵横比,
x, = sxx + tx y, = syy + ty ,
是一种受限形式的仿射变换。不幸的是,它不能与表2.1中列出的群干净地嵌套在一起。
平面表面流。该八参数变换(Horn1986;Bergen、Anandan等人1992;Girod、Greiner和Niemann2000),
x, = a0 + a1 x + a2 y + a6 x2 + a7 xy y, = a3 + a4 x + a5 y + a6 xy + a7 y2 ,
当一个平面表面发生小的三维运动时,就会产生这种误差。因此,可以认为它是对完整单应性的小运动近似。它的主要优点是它在运动参数ak中是线性的,而这些参数通常是被估计的量。
双线性插值。这种八参数变换(Wolberg1990),
x, = a0 + a1 x + a2 y + a6 xy y, = a3 + a4 x + a5 y + a7 xy,
可以用来插值由于正方形四个角点运动引起的变形。(实际上,它可以插值任何四个非共线点的运动。)虽然变形与运动参数呈线性关系,但通常不会保持直线(仅保持与正方形轴平行的直线)。然而,它在使用样条插值稀疏网格时非常有用(第9.2.2节)。
三维坐标变换集与二维变换集非常相似,总结在表2.2中。与二维一样,这些变换形成一个嵌套的组集。Hartley和Zisserman(2004,第2.4节)给出了这个层次结构的更详细描述。
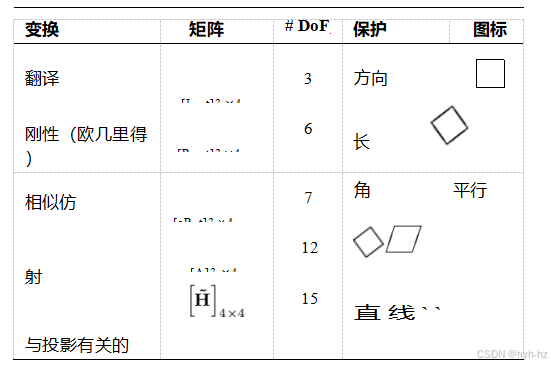
表2.2三维坐标变换层次。每个变换还保留了其下方行中列出的属性,即相似性不仅保持角度,还保持平行性和直线。3×4矩阵通过增加第四个[0T 1]行扩展为完整的4×4矩阵,用于齐次坐标变换。助记图标以二维形式绘制,但旨在表示在完整的三维立方体中发生的变换。
转换。3D转换可以写成xI = x + t或
(2.23)
其中I是(3×3)单位矩阵。
旋转+平移。也称为三维刚体运动或三维欧几里得变换或SE(3),可以写为xI = Rx + t或
(2.24)
其中R是一个3×3的正交旋转矩阵,满足RRT = I且jRj = 1。注意有时用下面的方法来描述刚体运动更为方便
xI = R (x - c) = Rx - Rc; (2.25)
其中c是旋转中心(通常是摄像机中心)。
紧凑地参数化三维旋转是一项非平凡的任务,我们在下面更详细地描述了这一点。
旋转尺度。三维相似变换可以表示为x,= sRx + t,其中s是任意的尺度因子。它也可以写成
(2.26)
这种变换保持了直线和平面之间的角度。
仿射变换。仿射变换写为x,= Ax-,其中A是任意的3×4矩阵,即
(2.27)
平行线和平面在仿射变换下保持平行。
投影变换。这种变换也被称为三维透视变换、同态变换或共线变换,它作用于齐次坐标,
= ~x, (2.28)
其中是一个任意的4×4齐次矩阵。与二维一样,得到的结果是齐次的 必须进行归一化处理
,以获得非均匀结果x。透视变换保持直线(即,变换后仍为直线)。
2D和3D坐标变换之间的最大区别在于,3D旋转矩阵R的参数化不是那么直接,因为存在几种不同的可能性。
欧拉角
旋转矩阵可以由绕三个主轴的三次旋转相乘形成,例如x、y和z轴,或者x、y和x轴。这通常不是一个好主意,因为结果取决于变换应用的顺序。更糟糕的是,在参数空间中平滑移动并不总是可能的,即有时一个或多个欧拉角会因旋转的小变化而剧烈改变。因此,我们甚至不

本书给出了欧拉角的公式,感兴趣的读者可以查阅其他教科书或技术报告(Faugeras1993;Diebel2006)。请注意,在某些应用中,如果已知旋转是一组单轴变换,则它们总是可以使用一组显式的刚体变换来表示。
轴/角度(指数扭转)
一个旋转可以用一个旋转轴和一个角度θ来表示,或者等效地用一个三维向量! = θ来表示。图2.5显示了如何计算等效的旋转。首先,我们将向量v投影到轴上以获得
v Ⅱ = (· v) = (^n^nT )v; (2.29)
v丄=v-vⅡ=(I-^n^nT)v。 (2.30)
我们可以使用交叉积将这个向量旋转90°,
v × = × v丄 = × v = [] × v; (2.31)
其中[]×是向量=(x;y;z)的叉积算子的矩阵形式,
(2.32)
注意,将这个向量再旋转90°等同于再次取交叉积,
v ×× = × v × = []v =
—v丄 ;
因此
v Ⅱ = v - v丄 = v + v ×× = (I + []
现在我们可以计算旋转向量u的平面内分量
u丄=cosθv丄+sinθv×=(sin θ[]×- cos θ[])v.
将所有这些项放在一起,我们得到最终的旋转向量
u=u丄+ vⅡ =(I + sin θ[]×+(1 - cos θ)[])v
. (2.33)
因此,我们可以写出围绕轴旋转θ的旋转矩阵
作为
R(,θ)= I + sin θ[]×+(1 - cos θ)[],
(2.34)
这被称为罗德里格斯公式(Ayache1989)。
轴和角度θ的乘积,! = θ =(ωx,ωy,ωz),是一个最小的代表-
用于三维旋转。通过常见的角度如90°的倍数进行旋转时,如果θ以度为单位存储,可以精确表示(并转换为精确矩阵)。不幸的是,这种表示并不唯一,因为我们可以总是加上360°(2π弧度)的倍数。
θ和得到相同的旋转矩阵。同样地,(,θ)和(-,-θ)表示相同的旋转。
但是,对于小旋转(例如,对旋转的修正),这是一个很好的选择。
特别是对于小(无穷小或瞬时)旋转和以弧度表示的θ,Rodrigues公式简化为
这给出了旋转参数!和R之间的一个很好的线性关系。我们也可以写成R(!)v≈v +!×v,当我们想要计算Rv关于!的导数时,这个公式非常方便。
(2.36)
另一种推导有限角度旋转的方法称为指数扭转(Murray,Li,and Sastry1994)。一个角度θ的旋转等同于k个角度θ/k的旋转。当k→∞时,我们得到
(2.37)

图2.6单位四元数位于单位球ⅡqⅡ = 1上。该图显示了通过三个四元数q0、q1和q2的平滑轨迹。q2的对径点,即-q2,表示与q2相同的旋转。
如果我们把矩阵指数展开为泰勒级数(使用恒等式[]+
2 =—[,
k > 0,再次假设θ是弧度),
(2.38)
这就产生了熟悉的罗德里格斯公式。
在机器人学(和群论)中,旋转被称为SO(3),即三维空间中的特殊正交群。增量旋转与李代数se(3)相关联,是构建旋转导数和建模旋转估计不确定性时的首选方法(Blanco2019;Sola、Deray和Atchuthan2019)。
单位四元数
单位四元数表示与角度/轴表示密切相关。单位四元数是一个长度为1的4维向量,其分量可以写成q =(qx,qy,qz,qw)或简写为q =(x,y,z,w)。单位四元数位于单位球ⅡqⅡ = 1上,而对偶(符号相反)的四元数q和—q表示相同的旋转(图2.6)。除了这种歧义(对偶覆盖)外,旋转的单位四元数表示是唯一的。此外,该表示是连续的,即随着旋转矩阵的连续变化,可以找到一个连续的四元数表示,尽管在四元数球上的路径可能会绕一圈再回到原点qo =(0,0,0,1)。对于
由于这些原因以及其他原因,四元数是计算机图形中用于姿态和姿态插值的非常流行的表示方法(Shoemake1985)。
四元数可以通过公式从轴/角度表示法推导出来
(2.39)
其中θ是旋转轴和角度。利用三角恒等式sin θ =
2 sin cos
2,罗德里格斯
公式
可以转换为
R(,θ)= I + sin θ[]×+(1—cos θ)[]
= I + 2w[v]× + 2[v] .
(2.40)
这表明使用一系列交叉乘积,通过四元数快速旋转向量v,
缩放和添加。为了得到R(q)作为(x,y,z,w)的函数的公式,回想一下
因此,我们得到
对角项可以通过用(x2+w2-y2-z2)等替换1-2(y2+z2)来使其更加对称。
单位四元数最吸引人的地方在于,它提供了一种简单的代数方法来组合以单位四元数表示的旋转。给定两个四元数q0 =(v0,w0)和q1 =(v1,w1),四元数乘法运算符定义为
q2 = q0 q1 = (v0 × v1 + w0 v1 + w1 v0 , w0 w1 — v0 · v1 ), (2.42)
具有这样的性质:R(q2)= R(q0)R(q1)。注意,四元数乘法不是交换的,就像三维旋转和矩阵乘法不是一样。
取四元数的逆很简单:只需翻转v或w的符号(但不能同时翻转!)。
(你可以验证这具有在(2.41)中置换R矩阵的预期效果。)因此,我们也可以定义四元数除法为
q2 = q0 /q1 = q0 q 1 = (v0 × v1 + w0 v1 — w1 v0 , —w0 w1 — v0 · v1 ). (2.43)
| 1. qr = q1 /q0 = (vr ; wr ) 2.如果wr < 0,则qr←—qr 3. θr = 2 tan-1(Ⅱvr Ⅱ/wr) 4. r = N (vr) = vr /Ⅱvr Ⅱ 5. θα = Q θr 6. qα =(sin θ r;cos θ) |
算法2.1球面线性插值(slerp)。首先根据四元数比例计算轴和总角度。(此计算可以移出生成动画中一组插值位置的内循环。)然后计算增量四元数,并将其乘以起始旋转四元数。
当需要两个旋转之间的增量旋转时,这很有用。
特别是,如果我们想要确定两个给定旋转之间的中间旋转,可以计算增量旋转,取角度的一部分,然后计算新的旋转。这个过程称为球线性插值或简称slerp(Shoemaker1985),并在算法2.1中给出。请注意,Shoemaker提出了除这里给出的公式外的两个其他公式。第一个公式是先将qr指数化为alpha,然后再乘以原始四元数,
q2 = qq0 ; (2.44)
而第二种方法是将四元数视为球面上的4维向量并使用
(2.45)
其中θ = cos-1(q0·q1),点积直接作用于四元数的四维向量之间。所有这些公式都能给出相似的结果,但当q0和q1接近时需要特别小心,这也是我更倾向于使用反正切来确定旋转角度的原因。
哪种旋转表示法更好?
三维旋转的表示方式的选择部分取决于应用。
轴/角表示是最简化的,因此不需要对参数施加任何额外的约束(无需每次更新后重新归一化)。如果角度以度数表示,更容易理解姿态(例如,绕儿轴旋转90°),也更容易表达精确的旋转。当角度以弧度表示时,可以轻松计算R关于θ的导数(2.36)。
另一方面,如果你想跟踪一个平滑移动的摄像机,四元数会更好,因为表示中没有不连续性。它也更容易在旋转之间插值,并且可以链接刚体变换(Murray、Li和Sastry 1994;Bregler和Malik 1998)。
我通常倾向于使用四元数,但要使用第11.2.2节中描述的增量旋转来更新其估计值。
既然我们已经知道如何表示二维和三维几何基元以及如何在空间中变换它们,接下来需要确定三维基元如何投影到图像平面上。我们可以使用线性三维到二维投影矩阵来实现这一点。最简单的模型是正交投影,它不需要除法就能得到最终(非齐次)结果。更常用的模型是透视投影,因为这种模型更能准确模拟真实相机的行为。
正字法和旁视角
正交投影就是将三维坐标p的z分量丢弃,得到二维点x。(在本节中,我们用p表示三维点,用x表示二维点。)可以写为
x = [I2×2 j0] p. (2.46)
如果我们使用的是齐次(射影)坐标系,我们可以写成
(2.47)
即,我们舍弃z分量,但保留w分量。正射投影是长焦距(远摄)镜头和相对于相机距离较浅的物体的近似模型(Sawhney和Hanson1991)。它仅对远心镜头精确(Baker和Nayar1999,2001)。

图2.7常用投影模型:(a)三维视图,(b)正射投影,(c)缩放正射投影,(d)平行透视,(e)透视,(f)物体中心。每个图都展示了投影的俯视图。请注意,在非透视投影中,地面平面和盒子侧面的平行线仍然保持平行。
在实际操作中,世界坐标(可能以米为单位测量尺寸)需要进行缩放才能适应图像传感器(物理上以毫米为单位测量,但最终是
以像素为单位)。因此,缩放正字法实际上更常用,
x = [sI2×2 j0] p. (2.48)
该模型相当于首先将世界点投影到局部前视平行图像平面上,然后使用常规透视投影对该图像进行缩放。这种缩放可以适用于场景的所有部分(图2.7b),也可以针对独立建模的对象进行不同的缩放(图2.7c)。更重要的是,在从运动中估计结构时,缩放可以在帧与帧之间变化,这能更好地模拟物体接近相机时发生的尺度变化。
正交坐标是一种流行的模型,用于重建远离相机的物体的三维形状,因为它大大简化了某些计算。例如,姿态(相机方向)可以使用简单的最小二乘法进行估计(第11.2.1节)。在正交坐标下,结构和运动可以通过分解(奇异值分解)同时进行估计,如第11.4.1节所述(Tomasi和Kanade 1992)。
一个密切相关投影模型是旁透视(Aloimonos1990;Poelman和Kanade1997)。在这个模型中,物体点首先被投影到与图像平面平行的局部参考线上。然而,它们并不是正交于该平面地投影,而是平行于视线方向投影到物体中心(图2.7d)。随后,这些点再进行常规的投影到最终的图像平面上,这实际上相当于缩放。因此,这两种投影的组合是仿射的,可以表示为
(2.49)
注意,三维中的平行线在Figure2.7b-d投影后仍然保持平行。与缩放正交法相比,平行透视提供了一个更精确的投影模型,而无需增加每像素透视分割的复杂性,后者会破坏传统的分解方法(Poelman和Kanade1997)。
前景
在计算机图形学和计算机视觉中,最常用的投影是真实三维透视(图2.7e)。在这里,通过将点除以它们的坐标来将其投影到图像平面上。
(2.50)
在齐次坐标中,投影具有简单的线性形式,
(2.51)
即,我们丢弃p的w分量。因此,在投影之后,无法恢复三维点与图像的距离,这对于二维成像传感器来说是有意义的。
计算机图形系统中常见的形式是两步投影,首先将三维坐标投影到归一化的设备坐标(x,y,z)∈[—1,1]×[—1,1]×[0,1],然后使用视口变换将这些坐标重新缩放为整像素坐标(Watt1995;OpenGL-ARB1997)。(初始)透视投影随后用一个4×4矩阵表示。
其中znear和zfar分别是近裁剪平面和远裁剪平面,zrange = zfar—znear。请注意,前两行实际上通过焦距和宽高比进行了缩放,使得可见光线被映射到(x,y,z)∈[—1,1]²。保留第三行而不是删除它的原因是,诸如z缓冲区等可见性操作需要为每个正在渲染的图形元素提供深度信息。
如果我们设置znear = 1,zfar→∞,并交换第三行的符号,归一化屏幕向量的第三个元素就会变成逆深度,即视差(Okutomi和Kanade 1993)。这在许多情况下非常方便,因为对于户外移动的相机而言,相对于相机的逆深度通常比直接的三维距离参数化更为稳定。
虽然普通的二维图像传感器无法测量到表面点的距离,但测距传感器(第13.2节)和立体匹配算法(第12章)可以计算这些值。然后,利用4×4矩阵的逆(第2.1.4节),可以直接将基于传感器的深度或视差值d映射回三维位置,这非常方便。如果我们使用满秩的4×4矩阵来表示透视投影,就可以实现这一点,如公式(2.64)所示。

p. Oc是光学中心(节点点),cs是传感器平面坐标系的三维原点,sx和sy是像素间距。
摄像头内参
一旦我们使用投影矩阵通过理想针孔投射出一个三维点,仍需根据像素传感器间距和传感器平面与原点的相对位置来变换所得坐标。图2.8展示了涉及的几何关系。在本节中,我们首先介绍从二维像素坐标到三维光线的映射,使用传感器单应性矩阵Ms,因为这更容易用物理可测量的量来解释。然后,我们将这些量与更常用的相机内参矩阵K联系起来,该矩阵用于将以相机为中心的三维点pc映射到二维像素坐标。
图像传感器返回由整数像素坐标(儿s;ys )索引的像素值,通常坐标从图像的左上角开始向下向右移动。(这一惯例并非所有成像库都遵循,但对其他坐标系的调整是直截了当的。)为了将像素中心映射到三维坐标,我们首先根据像素间距(sx;sy)(对于固态传感器有时以微米表示)缩放(儿s;ys)值,然后用原点cs和三维旋转Rs描述传感器阵列相对于相机投影中心Oc的方向(图2.8)。
组合的二维到三维投影可以写为
(2.53)
3×3矩阵Ms的前两列是图像像素阵列沿儿s和ys方向的单位步长对应的三维向量,而第三列是三维
矩阵Ms由八个未知数参数化:三个描述旋转的参数Rs,三个描述平移的参数cs,以及两个缩放因子(sx;sy)。请注意,这里我们忽略了图像平面上两轴之间的倾斜可能性,因为固态制造技术使得这一点可以忽略不计。实际上,除非我们有传感器间距或传感器方向的精确外部知识,否则只有七个自由度,因为仅凭外部图像测量无法区分传感器与原点的距离和传感器间距。
然而,估计具有所需7个自由度的相机模型Ms(即,在适当重新缩放后,前两列是正交的)是不切实际的,因此大多数实践者假设一个通用的3×3齐次矩阵形式。
3D像素中心点p与3D相机中心点pc之间的关系由未知缩放比例s给出,p = spc。因此,我们可以将pc s的完整投影写为
从上述讨论中,我们看到理论上K有七个自由度,而在实践中则有八个自由度(即一个3×3齐次矩阵的全部维度)。那么,为什么大多数关于三维计算机视觉和多视图几何的教科书(如Faugeras 1993;Hartley和Zisserman 2004;Faugeras和Luong 2001)将K视为具有五个自由度的上三角矩阵呢?
虽然这些书中通常没有明确说明,但这是因为我们无法仅凭外部测量恢复完整的K矩阵。当基于外部3D点或其他测量(Tsai1987)校准相机时(第11.1节),最终会使用一系列测量同时估计相机的内参(K)和外参(R;t),
(2.55)
P = K[Rjt] (2.56)
被称为相机矩阵。检查这个方程,我们看到我们可以后乘
用R1对K进行乘法运算,再用R对[Rjt]进行乘法运算,最终得到一个有效的校准。因此,它
仅根据图像测量值无法知道传感器的真实方向和相机的真内参。

图2.9简化的相机内参,显示焦距f和图像中心(cx,cy)。图像宽度和高度为W和H。
选择K的上三角形式似乎是惯例。给定一个完整的3×4相机矩阵P = K[Rjt],我们可以使用QR分解计算出一个上三角的K矩阵(Golub和Van Loan 1996)。(请注意术语上的不幸冲突:在矩阵代数教科书中,R表示一个上三角(对角线右侧)矩阵;而在计算机视觉中,R是一个正交旋转。)
有几种方法可以写出K的上三角形式。一种可能性是
(2.57)
使用独立的焦距fx和fy来表示传感器的x和y方向。条目s编码了由于传感器未垂直安装在光轴上而可能产生的传感器轴之间的偏斜,(cx,cy)表示以像素坐标表示的图像中心。在计算机视觉文献中,图像中心也常被称为主点(Hartley和Zisserman 2004),尽管在光学领域,主点是通常位于镜头内部、主平面与主(光学)轴相交处的三维点(Hecht 2015)。另一种可能性是
(2.58)
其中,已经明确地给出了纵横比a,并且使用了共同的焦距f。
在实践中,对于许多应用,通过设置=1可以获得更简单的形式
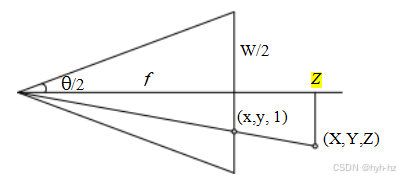
图2.10中心投影,显示了3D和2D坐标p和x之间的关系,以及焦距f、图像宽度W和水平视场θH之间的关系。
且s = 0,
通常,将原点设置在图像的大致中心处,例如,(cx,cy)=(W/2,H/2),其中W和H分别是图像的宽度和高度,可以产生一个具有单个未知数的完美可用的相机模型,即焦距f。
图2.9展示了这些量如何作为简化成像模型的一部分进行可视化。请注意,现在我们将图像平面置于节点点(镜头的投影中心)之前。y轴的方向也进行了反转,以获得与大多数成像库处理垂直(行)坐标方式相兼容的坐标系。
关于焦距的说明
如何表达焦距的问题常常在计算机视觉算法的实现和讨论结果时引起混淆,这是因为焦距取决于用来测量像素的单位。
如果我们用整数值来编号像素坐标,比如[0,W)×[0,H),那么焦距f和相机中心(cx,cy)在公式(2.59)中就可以表示为像素值。这些量与摄影师常用的焦距有什么关系呢?
图2.10说明了焦距f、传感器宽度W和水平视场θH之间的关系,它们遵循公式
对于传统的35毫米胶片相机,其有效曝光面积为24毫米×36毫米,因此W=36毫米,所以f也以毫米表示。例如,单反(单镜头反光)相机常用的“标准”镜头焦距是50毫米,这是一个很好的长度,而85毫米则是人像摄影的标准焦距。然而,由于我们处理的是数字图像,因此用像素来表示W更为方便,这样焦距f可以直接用于校准矩阵K中,如公式(2.59)所示。
另一种可能性是调整像素坐标,使其沿较长的图像维度变化范围为[-1,1),沿较短的轴变化范围为[-a-1,a-1],其中a≥1是图像宽高比(与前面介绍的传感器单元宽高比相反)。这可以通过使用修改后的归一化设备坐标来实现,
=(2xs - W)/S和ys,=(2ys - H)/S,其中S = max(W,H)。(2.61)
这有一个优点,即焦距f和图像中心(cx,cy)不再依赖于图像分辨率,这在使用多分辨率图像处理算法时非常有用,例如图像金字塔(第3.5节)。使用S而不是W还使得风景(水平)和人像(垂直)照片的焦距相同,就像35毫米摄影中那样。(在某些计算机图形学教科书和系统中,归一化设备坐标范围为[-1,1]×[-1,1],这需要使用两个不同的焦距来描述相机内参(Watt1995)。)将S = W = 2代入(2.60),我们得到更简单的(无量纲的)关系。
(2.62)
各种焦距表示之间的转换是直接的,例如,从无单位的f到以像素表示的f,乘以W/2,而从以像素表示的f转换为等效的35mm焦距,乘以18mm。
既然我们已经展示了如何参数化校准矩阵K,那么我们可以将相机内参和外参组合在一起,得到一个单一的3×4相机矩阵

(平面)。
有时最好使用可逆的4×4矩阵,可以通过不删除P矩阵的最后一行来获得,
(2.64)
其中E是一个三维刚体(欧几里得)变换,是满秩校准矩阵。4×4的相机矩阵可以直接将三维世界坐标p-w =(xw,yw,zw,1)映射到屏幕坐标(加上视差),xs =(xs,ys,1,d),
xs ~ p-w , (2.65)
其中~表示在比例上相等。注意,在乘以之后,向量被除以向量的第三个元素,以获得归一化形式xs =(xs,ys,1,d)。
一般来说,使用4×4矩阵时,我们可以自由地将最后一行重新映射为任何适合我们的用途(而不仅仅是作为视差的“标准”解释,即逆深度)。让我们将最后一行重写为p3 = s3 [0 Ic0],其中Ⅱ0Ⅱ = 1。然后我们有如下方程
其中z = p2·p-w = rz·(pw - c)是pw从相机中心C(2.25)沿光轴Z的距离(图2.11)。因此,我们可以将d解释为参考平面0·pw + c0 = 0上的三维场景点pw的投影视差或投影深度(Szeliski和Coughlan 1997;Szeliski和Golland 1999;Shade,Gortler等1998;Baker,
Szeliski和Anandan1998)。(投影深度有时也被称为视差
使用“平面加视差”一词的重建算法(Kumar,Anandan和Hanna
1994;Sawhney1994)。)设置0 = 0和c0 = 1,即把参考平面置于无穷远,
结果是更标准的d = 1/z版本的视差(Okutomi和Kanade1993)。
另一种方法是将矩阵反转,这样我们就可以映射像素加视差
直接返回到3D点,
. (2.67)
一般来说,我们可以选择任何方便的形式,即使用任意投影来采样空间。这在设置多视图立体重建算法时特别有用,因为它允许我们通过一系列平面(第12.1.2节)在空间中进行扫描,采用可变(投影)采样,以最佳匹配感知到的图像运动(Collins1996;Szeliski和Golland1999;Saito和Kanade1999)。
当我们从不同的摄像机位置拍摄一个三维场景的两个图像时会发生什么
方向(图2.12a)?使用来自(2.64)的4×4相机矩阵=E的满秩,
~ 0 E0 p = 0 p. (2.68)
假设我们已知一个图像中像素的z缓冲区或视差值d0,我们可以使用以下公式计算三维点位置p:
p ~ E0-10-10
(2.69)
~ 1 E1 p = 1 E1 E0-10-10
= 1 0-10
(2.70)
不幸的是,我们通常无法获得常规摄影图像中像素的深度坐标。但是,对于平面场景,如上文(2.66)所述,我们可以
用一般平面方程0·p + c0替换(2.64)中P0的最后一行,该方程可以映射
平面上的点对应于d0 = 0的值(图2.12b)。因此,如果我们设d0 = 0,就可以忽略M10中的最后一列(2.70)及其最后一行,因为我们不关心最终的Z缓冲区深度。映射方程(2.70)因此简化为

图2.12一个点被投影到两个图像中:(a)三维点坐标(X,Y,Z,1)与二维投影点(x,y,1,d)之间的关系;(b)平面单应性引起的
所有点都在一个公共平面上0·p + c0 = 0。
其中,1 0 是一般3×1 0现在是
2D
均匀坐标(即,3-向量)(Szeliski1996)。这证明了使用8参数均匀模型作为平面场景马赛克的一般对齐模型是合理的(Mann和Picard1994;Szeliski1996)。
在不需要知道深度就能执行相机间映射的另一种特殊情况下,就是当相机进行纯旋转时(第8.2.3节),即t0 = t1。在这种情况下,我们可以写
1 ~ K1
R1 R0-1K0-10 =
K1 R10 K0-10
对象中心投影
使用长焦镜头时,仅凭图像测量来可靠地估算焦距往往变得困难。这是因为焦距与物体距离高度相关,很难将这两种效应区分开来。例如,通过变焦远摄镜头观察到的物体比例变化,可能是由于变焦变化或向用户靠近造成的。(这种效果在阿尔弗雷德·希区柯克的电影《迷魂记》中被戏剧性地运用,同时变焦和摄像机运动的变化产生了令人不安的效果。)
如果我们写出与之对应的投影方程,这种模糊性就变得更加清晰了
其中,rx、ry和rz是R的三行。如果到物体中心的距离tz≥ⅡpⅡ(即物体的大小),则分母近似为tz,投影物体的整体比例取决于f与tz的比值。因此,这两个量很难区分。
为了更清楚地看到这一点,设ηz = tz-1和s = ηz f。然后我们可以将上面的方程重写为
(Szeliski和Kang 1994;Pighin、Hecker等1998)。如果我们观察的是已知物体(即,三维坐标p已知),则可以可靠地估计投影尺度s。逆距离ηz现在大多与s的估计值脱钩,可以从物体旋转时的透视缩短量来估算。此外,随着镜头变长,即投影模型变为正射投影,无需用正射投影模型替换透视成像模型,因为可以使用相同的方程,且ηz→0(而f和tz都趋向于无穷大)。这使得我们能够自然地建立正射重建技术(如分解)与其投影/透视对应技术之间的联系(第11.4.1节)。
上述成像模型均假设相机遵循线性投影模型,即世界中的直线在图像中也是直线。(这是由于线性矩阵运算应用于齐次坐标而自然得出的结果。)不幸的是,许多广角镜头存在明显的径向畸变,这表现为直线投影中的可见曲率。(有关镜头光学的更详细讨论,包括色差,请参见第2.2.3节。)如果不考虑这种畸变,就无法创建高度准确的逼真重建。例如,未考虑径向畸变构建的图像马赛克通常会因对应特征在像素融合前的错位而产生模糊(第8.2节)。
幸运的是,在实际操作中,补偿径向畸变并不那么困难。对于大多数镜头而言,一个简单的四次方畸变模型就能产生良好的效果。设(xc,yc)是透视分割后但在焦距f缩放和图像中心(cx,cy)移动前获得的像素坐标,即,
径向畸变模型指出,观测图像中的坐标会根据其径向距离的大小而向中心偏移(桶形畸变)或远离中心(枕形畸变)(图2.13a-b)。最简单的径向畸变模型使用低阶多项式,例如:
c = yc (1 + h1 r + h2 r),
其中r = x + y,h1和h2称为径向畸变参数。7该模型,
该模型还包括一个切向分量,以考虑透镜偏心,最初由Brown(1966)在摄影测量文献中提出,因此有时被称为Brown或Brown-Conrady模型。然而,通常忽略畸变的切向分量,因为它们可能导致估计不那么稳定(Zhang2000)。
径向畸变步骤之后,可以使用以下公式计算最终像素坐标
xs = fc + cx ys = fc + cy .
如第11.1.4节所述,可以使用多种技术来估计给定透镜的径向畸变参数。
有时,上述简化模型无法准确模拟复杂透镜产生的真实畸变(尤其是在非常宽的角度下)。更完整的分析模型还包括切向畸变和偏心畸变(Slama1980)。
7有时,xc和c之间的关系是反过来的,即xc = c(1 + 1 +
2).如果我们通过除以f将图像像素映射到(扭曲的)光线中,这是很方便的。然后我们可以消除畸变
光线和空间中的真实3D光线。

图2.13径向镜头畸变:(a)桶形、(b)枕形和(c)鱼眼。鱼眼
图像从侧面到侧面跨度近180°。
偏离光轴的角的投影(Xiong和Turkowski,1997),
r = f θ; (2.80)
这与方程(8.55–8.57)描述的极坐标投影相同。由于从中心到视点的距离(像素)与视角之间的映射主要呈线性关系,这类镜头有时被称为f-θ镜头,这可能是流行的RICOH THETA 360°相机得名的原因。熊和图尔科夫斯基(1997)描述了如何通过在φ中增加一个额外的二次校正来扩展这一模型,以及如何使用直接(基于强度的)非线性最小化算法从一组重叠的鱼眼图像中估计未知参数(投影中心、缩放因子等)。
对于更大、更不规则的畸变,可能需要使用样条函数的参数化畸变模型(Goshtasby1989)。如果透镜没有单一的投影中心,可能需要分别建模每个像素对应的三维线(而不是方向)(Gremban,Thorpe和Kanade1988;Champleboux,Lavall e等1992a;Grossberg和Nayar2001;Sturm和Ramalingam2004;Tardif,Sturm等2009)。这
技术中的一些在第11.1.4节中有更详细的描述,该节讨论了如何校准透镜畸变。
有一个与简单的径向畸变模型相关的微妙问题,通常被轻描淡写地忽略。我们引入了透视投影和最终传感器阵列投影步骤之间的非线性关系。因此,一般来说,我们无法将任意的3×3矩阵K乘以一个旋转矩阵,使其变为上三角形式并将其吸收进全局旋转中。然而,这种情况并没有乍看之下那么糟糕。对于许多应用而言,保持简化后的对角线形式(2.59)仍然是一个合适的模型。此外,如果我们纠正径向和其他畸变到能够保留直线的程度,我们有

图2.14光度图像形成的简化模型。光由一个或多个光源发出,然后从物体表面反射。这部分光线的一部分被导向相机。这个简化模型忽略了多次反射,这在现实场景中经常发生。
基本上将传感器转换回线性成像器,之前的分解仍然适用。
在建模图像形成过程时,我们描述了世界中的三维几何特征如何投影到图像中的二维特征。然而,图像并不是由二维特征组成的。相反,它们是由离散的颜色或强度值构成的。这些值来自哪里?它们与环境中的光照、表面属性和几何形状、相机光学以及传感器特性(图2.14)有何关系?在本节中,我们将开发一套模型来描述这些相互作用,并制定图像形成的生成过程。关于这些主题的更详细讨论可以在计算机图形学和图像合成的教科书中找到(Cohen和Wallace 1993;Sillion和Puech 1994;Watt 1995;Glassner 1995;Weyrich,Lawrence等2009;Hughes,van Dam等2013;Marschner和Shirley 2015)。
图像离不开光。要生成图像,场景必须被一个或多个光源照亮。(某些模式如荧光显微镜和X射线断层扫描不符合这一模型,但本书不涉及这些。)光源通常可以分为点光源和面光源。
点光源起源于空间中的单一位置(例如,一个小灯泡),也可能位于无穷远处(例如,太阳)。(请注意,在某些应用中,如模拟柔和阴影(半影),太阳可能需要被视为一个区域光源。)除了位置外,点光源还具有强度和色谱,即波长分布L(λ)。光源的强度随光源与被照亮物体之间距离的平方而衰减,因为相同的光被分散到更大的(球形)区域。光源还可能有方向衰减(依赖性),但在我们的简化模型中忽略这一点。
区域光源更为复杂。一个简单的区域光源,如带有扩散器的荧光天花板灯,可以建模为一个有限的矩形区域,向所有方向均匀发光(Cohen和Wallace 1993;Sillion和Puech 1994;Glassner 1995)。当分布强烈定向时,可以使用四维光场来替代(Ashdown 1993)。
更复杂的光照分布,例如,可以近似表示坐在室外庭院中的物体上的入射光照,通常可以用环境映射(Greene1986)(最初称为反射映射(Blinn和Newell1976))来表示。
将入射光的方向映射到颜色值(或波长,λ),
L( ; λ); (2.81)
并且等同于假设所有光源都位于无穷远处。环境贴图可以表示为一组立方体面(Greene 1986),也可以表示为单个经纬度图(Blinn和Newell 1976),或者表示为反射球的图像(Watt 1995)。获取真实环境贴图的大致模型的一种便捷方法是拍摄一个反射镜面球的图像(有时会附带一个较暗的球以捕捉高光),然后将此图像解包到所需的环境贴图上(Debevec 1998)。Watt(1995)对环境映射进行了很好的讨论,包括用于将方向映射到像素的三个最常用表示形式所需的公式。
当光线照射到物体表面时,会发生散射和反射(图2.15a)。为了描述这种相互作用,已经开发了多种模型。在本节中,我们首先介绍最通用的形式——双向反射分布函数,然后探讨一些更专业的模型,包括漫反射、镜面反射和Phong着色模型。我们还将讨论如何利用这些模型来计算场景对应的全局光照。
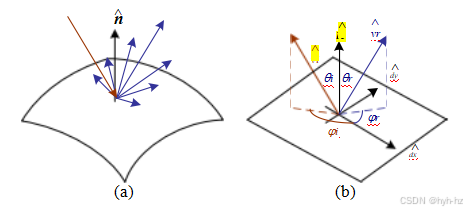
图2.15 (a)光照射到表面时发生散射。(b)双向反射率分布函数(BRDF)f(θi;φi;θr;φr)由入射角参数化。
与局部表面坐标系方向相交、i和反射、r光线方向
(x ; y ; ).
双向反射分布函数(BRDF)
最普遍的光散射模型是双向反射率分布函数(BRDF)。相对于表面的某个局部坐标系,BRDF是一个四维函数,描述了每个波长到达入射方向i的部分在反射方向r中的发射量(图2.15b)。该函数可以用入射方向和反射方向相对于表面坐标系的角度来表示。
fr (θi ; φi ; θr ; φr ; λ). (2.82)
BRDF是互易的,即由于光传输的物理特性,可以交换i和r的角色,仍然得到相同的结果(这有时被称为亥姆霍兹互易)。
大多数表面是各向同性的,即在光传输方面,表面上没有优先方向。(例外情况是各向异性表面,如拉丝(划痕)铝,其反射率取决于光线与划痕方向的关系。)对于各向同性材料,我们可以简化BRDF为
fr (θi;θr;jφr - φi j;λ)或fr (i;r;;λ); (2.83)

图2.16这张雕像的特写显示了漫反射(平滑阴影)和镜面反射(闪亮高光),以及由于光线可见度降低和相互反射而造成的凹槽和褶皱变暗。(照片由加州理工学院视觉实验室提供,http://www.vision.caltech.edu/archive.html。)
为了计算在给定光照条件下,从表面点p沿方向r射出的光量,我们需要积分入射光Li(i;λ)与BRDF的乘积(一些作者将这一步称为卷积)。考虑到缩短因子cos+ θi,我们得到
在哪里
cos+ θi = max (0; cos θi ). (2.85)
如果光源是离散的(有限数量的点光源),我们可以用求和代替积分
给定表面的BRDF可以通过物理建模(Torrance和Sparrow 1967;Cook和Torrance 1982;Glassner 1995)、启发式建模(Phong 1975;Lafortune、Foo等1997)或通过经验观察(Ward 1992;Westin、Arvo和Torrance 1992;Dana、van Ginneken等1999;Marschner、Westin等2000;Matusik、Pfister等2003;Dorsey、Rushmeier和Sillion 2007;Weyrich、Lawrence等2009;Shi、Mo等2019)获得。典型的BRDF通常可以分为漫反射和镜面反射两部分,如下所述。

图2.17 (a)由缩短引起的反射光减少取决于入射光方向i与表面法线之间的夹角的余弦值i·。(b)镜面(镜面反射):入射光线方向i沿表面法线反射到镜面方向^si。
漫射反射
漫射成分(也称为兰伯特反射或哑光反射)均匀地向各个方向散射光线,这是我们通常与阴影现象联系在一起的现象,例如,在观察雕像时所看到的表面法线上的平滑(非反光)强度变化(图2.16)。漫射反射还经常赋予光线强烈的体色,因为这是由物体材料内部选择性吸收和重新发射光线引起的(Shafer1985;Glassner1995)。
虽然光在所有方向上均匀散射,即BRDF是恒定的,
fd(i;r;;λ)= fd (λ); (2.87)
光的强度取决于入射光线方向与表面法线θi之间的角度。这是因为,在倾斜的角度下,相同光照面积会变得更大,当出射表面法线远离光源时,整个区域完全被遮挡(图2.17a)。(想象一下你如何面向太阳或壁炉以获得最大的温暖,以及手电筒斜射到墙上比直射时亮度低的情况。)因此,漫反射的阴影方程可以表示为
在哪里
[i·]+ = max(0,i·)。 (2.89)
典型BRDF的第二个主要组成部分是镜面(光泽或高光)反射,这强烈依赖于出射光的方向。考虑光线从镜面反射的情况(图2.17b)。入射光线沿表面法线旋转180°后被反射。使用与方程(2.29–2.30)相同的符号,我们可以计算镜面反射方向^si为
^si = v Ⅱ - v丄 = (2^n^nT - I)vi. (2.90)
因此,光线在给定方向r上的反射量取决于视向r与镜面方向^si之间的夹角θs = cos-1(r·^si)。例如,Phong(1975)模型使用了该角度余弦值的幂,
fs (θs ; λ) = ks (λ) coske θs , (2.91)
而Torrance和Sparrow(1967)的微面模型使用高斯,
fs (θs ; λ) = ks (λ) exp(-cθ). (2.92)
较大的指数ke(或逆高斯宽度cs )对应于具有明显高光的更多镜面表面,而较小的指数则更好地模拟具有较柔和光泽的材料。
光阴影
冯(1975)将反射的漫射和镜面成分与另一个术语结合,他称之为环境光照。这一术语解释了物体通常不仅受到点光源的照射,还受到与漫反射相关的普遍漫射光照的影响(例如房间内的墙壁)或远处的光源,如蓝天。在冯模型中,环境光项不依赖于表面的方向,而是取决于环境光照La (λ)和物体ka (λ)的颜色,
fa (λ) = ka (λ)La (λ). (2.93)

图2.18在固定入射光照方向下通过Phong着色模型BRDF的横截面:(a)分量值随偏离表面法线角度的变化;(b)极坐标图。Phong指数ke的值由“Exp”标签表示,光源与法线呈30°角。
图2.18显示了与表面法线(在包含光照方向和观察者平面内)成一定角度时的Phong着色模型组件的典型集合。
通常,环境反射色分布ka (λ)和漫反射色分布kd (λ)是相同的,因为它们都源自表面材料内部的次表面散射(体反射)(Shafer 1985)。镜面反射色分布ks (λ)通常是均匀的(白色),因为它由界面反射引起,不会改变光的颜色。(例外情况是金属材料,如铜,与更常见的电介质材料,如塑料相对。)
环境光照La (λ)通常与直接光源Li (λ)的颜色不同,例如,在晴朗的户外场景中可能是蓝色,而在用蜡烛或白炽灯照明的室内则可能是黄色。(阴影区域存在环境天空光照是导致阴影比相应亮部更蓝的原因)。还需注意的是,Phong模型(或任何阴影模型)中的漫反射成分取决于入射光源i的角度,而镜面反射成分则取决于观察者vr与镜面反射方向^si之间的相对角度(后者本身又取决于入射光方向i和表面法线)。
冯氏着色模型在物理精度方面已被计算机图形学中的新模型所超越,包括库克和托伦斯(1982)基于托伦斯和斯帕罗(1967)的原始微面模型开发的模型。最初,计算机图形硬件实现了冯氏模型,但可编程像素着色器的出现使得使用更复杂的模型成为可能。
Torrance和Sparrow(1967)的反射模型也是Shafer(1985)的双色反射模型的基础,该模型指出,从单一光源照射的均匀材料的表观颜色取决于两个项的总和,
即,界面反射光的辐射度Li和表面物体反射的辐射度Lb。每个辐射度都是相对功率谱c(λ)和几何量m(r;i;)的简单乘积,其中c(λ)仅依赖于波长,而m(r;i;)仅依赖于几何形状。(该模型可以通过假设单个光源且没有环境光照,并重新排列项,从广义版本的Phong模型中轻松推导出来。)双色模型已成功应用于计算机视觉领域,用于分割具有大阴影变化的镜面彩色物体(Klinker 1993),并启发了局部双色模型,例如拜耳模式去马赛克化(Bennett,Uyttendaele等2006)。
全局光照(光线追踪和辐射度)
迄今为止提出的简单阴影模型假设光线从光源发出,反射到可见于相机的表面,从而改变强度或颜色,最终到达相机。实际上,光源可能会被遮挡物遮住,光线在从光源到相机的路径中可能多次绕过场景。
传统上,有两种方法用于模拟此类效果。如果场景主要为镜面反射(经典例子包括玻璃物体和高抛光或镜面球体组成的场景),首选的方法是光线追踪或路径追踪(Glassner 1995;Akenine-Moeller和Haines 2002;Marschner和Shirley 2015),这种方法会从相机出发,沿着多条路径向光源(或反之)追踪单个光线。如果场景主要由均匀反照率的简单几何照明器和表面组成,则更倾向于使用辐射度(全局光照)技术(Cohen和Wallace 1993;Sillion和Puech 1994;Glassner 1995)。两种技术的结合也被开发出来(Walace、Cohen和Greenberg 1987),以及更为通用的光传输技术,用于模拟如波纹水面上投射的焦散等效果。
基本的光线追踪算法将光线与摄像机图像中的每个像素关联起来,并找到其与最近表面的交点。然后,可以使用前面介绍的简单着色方程(例如,公式(2.94))计算出主要贡献。
对于该表面元素可见的所有光源。(另一种计算哪些表面被光源照亮的技术是生成阴影贴图或阴影缓冲区,即从光源视角渲染场景,然后将渲染像素的深度与贴图进行比较(Williams 1983;Akenine-Mo...ller和Haines 2002)。)随后可以沿着镜面反射方向向场景中的其他物体投射额外的次级光线,同时跟踪镜面反射引起的任何衰减或颜色变化。
辐射度通过将亮度值与场景中的矩形表面区域(包括区域光源)关联起来工作。场景中任意两个(相互可见的)区域之间的光交换量可以被捕捉为一个形式因子,这取决于它们的相对位置和表面反射特性,以及随着光线分布到更大的有效球体中而产生的1/r²衰减(Cohen和Wallace 1993;Sillion和Puech 1994;Glassner 1995)。然后可以建立一个大型线性系统来求解每个区域块的最终亮度,使用光源作为强迫函数(右侧)。一旦系统求解完成,可以从任何所需视角渲染场景。在某些情况下,可以使用计算机视觉技术从照片中恢复场景的整体光照(Yu、Debevec等1999)。
基本辐射算法没有考虑某些近场效应,例如角落内的变暗和划痕,或者由于其他表面的部分遮挡而造成的有限环境光照。这些效应已经在许多计算机视觉算法中得到了利用(Nayar、Ikeuchi和Kanade 1991;Langer和Zucker 1994)。
虽然所有这些全局光照效果都可能对场景的外观产生强烈影响,从而影响其三维解释,但本书并未详细讨论这些内容。(但是,请参见第13.7.1节中关于从真实场景和物体恢复BRDF的讨论。)
一旦场景中的光线到达相机,它仍然必须通过镜头才能到达模拟或数字传感器。对于许多应用而言,将镜头视为一个理想的针孔就足够了,它只是将所有光线投射到一个共同的投影中心(图2.8和2.9)。
然而,如果我们要处理诸如焦点、曝光、暗角和像差等问题,我们需要开发一个更复杂的模型,这就是光学研究的切入点(Mo...ller1988;Ray2002;Hecht2015)。
图2.19显示了最基本的透镜模型的示意图,即由单片玻璃制成的薄透镜,其两侧曲率非常低且相等。根据透镜定律(可以通过光束折射的简单几何论证得出),
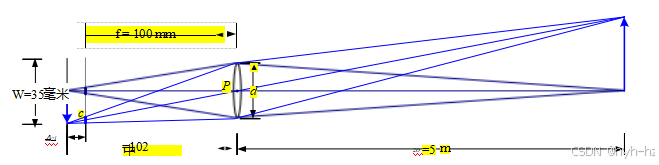
图2.19焦距为f的薄透镜将位于透镜前方距离zo的平面发出的光聚焦到距离zi的焦平面上(垂直灰线紧邻c)。当焦平面(垂直灰线紧邻c)向前
移动时,图像不再清晰,模糊圈(细长线段)取决于图像平面移动距离△zi与透镜孔径直径d之间的关系。视场(f.o.v.)取决于传感器宽度W与焦距f的比值(更精确地说,是聚焦距离zi,通常接近于f)。
物体到镜头的距离zo与成像在镜头后形成的距离zi之间的关系可表示为
, (2.97)
其中f称为透镜的焦距。如果我们让zo→∞,即调整透镜(移动像面),使无穷远处的物体处于焦点上,我们得到zi = f,这就是为什么我们可以认为焦距为f的透镜在近似情况下等同于距离焦平面f处的一个针孔(图2.10),其视场由公式(2.60)给出。
如果焦平面偏离其正确的对焦位置zi(例如,通过转动镜头上的对焦环),位于zo的物体将不再清晰,如图2.19中的灰色平面所示。失焦的程度由弥散圆c表示(在灰色平面上以短粗的蓝色线段表示)。弥散圆的方程可以通过相似三角形推导得出;它取决于焦平面内的移动距离△zi与原始对焦距离zi的关系以及光圈直径d(见练习2.4)。
场景中允许的深度变化,将模糊圈限制在可接受的数量,通常称为景深,是聚焦距离和光圈的函数,如许多镜头标记所示(图2.20)。由于这个

景深取决于光圈直径d,我们还必须知道它如何随通常显示的f数变化,通常表示为f/#或N,定义为
其中焦距f和孔径直径d以相同的单位(例如,毫米)测量。
通常写入光圈值的方法是将f/#中的#替换为实际数值,例如f/1.4、f/2、f/2.8、...、f/22。(或者,我们也可以表示为N = 1.4等。)一个简单的理解方法是注意到焦距除以光圈值等于光圈直径d,因此这些公式实际上就是光圈直径的计算公式。
请注意,f数字通常以全点表示,这些数字是√2的倍数,因为每次选择更小的f数字
,入口光圈的面积都会翻倍。(这种翻倍也称为曝光值或EV的变化。它对到达传感器的光线量的影响与将曝光时间加倍相同,例如从1/250增加到1/125;参见练习2.5。)
现在你已经知道如何在光圈系数和光圈直径之间进行转换,你可以根据焦距f、弥散圆c和焦点距离zo构建自己的景深图,如练习2.4所解释的那样,并观察这些图表与实际镜头上的观察结果有多吻合,例如图2.20中所示的镜头。
当然,真实的透镜并非无限薄,因此会受到几何像差的影响,除非使用复合元件来校正这些像差。经典的五种塞德尔像差,当使用三阶光学时产生,包括球面像差、彗差、散光、场曲和畸变(Mo...ller1988;Ray2002;Hecht2015)。

图2.21在受色差影响的透镜中,不同波长的光(例如红色和蓝色箭头)聚焦在不同的焦距f上,因此具有不同的深度zi,导致几何(平面内)位移和失焦。
由于玻璃的折射率随波长略有变化,简单的透镜会受到色差的影响,即不同颜色的光聚焦在略微不同的距离(因此放大倍数也略有不同),如图2.21所示。波长依赖的放大倍数,即横向色差,可以建模为每种颜色的径向畸变(第2.1.5节),因此可以使用第11.1.4节中描述的技术进行校准。由纵向色差引起的波长依赖模糊可以通过第10.1.4节中描述的技术进行校准。不幸的是,由纵向像差引起的模糊更难消除,因为高频成分会被强烈衰减,从而难以恢复。
为了减少色差和其他类型的像差,当今大多数摄影镜头都是由不同玻璃元件(带有不同涂层)组成的复合透镜。这些透镜不能再被建模为只有一个节点P,所有光线都必须通过这个节点(当用针孔模型近似透镜时)。相反,这些透镜既有前节点,光线从这里进入透镜,也有后节点,光线从这里离开并前往传感器。实际上,在进行仔细的相机校准时,只有前节点的位置是感兴趣的,例如,在确定旋转点以捕捉无视差全景图时(参见第8.2.3节和Littlefield(2006)及Houghton(2013))。
然而,并非所有镜头都能建模为具有单一节点。特别是像鱼眼镜头(第2.1.5节)和某些由透镜和曲面镜组成的折反射成像系统(Baker和Nayar 1999)这样的广角镜头,并没有一个所有获取光线都通过的单一点。在这种情况下,最好

图2.22光照射到面积δi的像素上的光量取决于孔径直径d与焦距f之比的平方,以及离轴角Q余弦的四次方cos4 Q。
如第2.1.5节所述,明确构建像素坐标与空间中的三维射线之间的映射函数(查找表)(Gremban、Thorpe和Kanade1988;Champleboux、Lavall e等人1992a;Grossber
和Nayar 2001;Sturm和Ramalingam 2004;Tardif、Sturm等人2009)。
暗角
现实世界中透镜的另一个特性是暗角,即图像亮度向图像边缘下降的趋势。
通常有两种现象对此效果有所贡献(Ray2002)。第一种称为自然暗角,是由于物体表面、投影像素和镜头光圈的缩短造成的,如图2.22所示。考虑从位于离轴角度Q处的大小为δo的物体表面区域发出的光线。因为这个区域相对于相机镜头被缩短了,到达镜头的光量减少了cos Q倍。到达镜头的光量还受到通常的1/r²衰减影响;在这种情况下,距离ro = zo / cos Q。实际通过光圈的面积被额外缩短了一个cos Q倍,即从点O看去,光圈是一个尺寸为d×d cos Q的椭圆。综合所有这些因素,我们看到从O发出并穿过光圈到达位于I的图像像素的光量与
由于三角形△OP Q和△IP J相似,物体表面δo和图像像素δi的投影面积与zo: zi成相同的(平方)比例,
将这些组合在一起,我们得到到达像素i的光量与孔径直径d、聚焦距离zi≈f和离轴角Q之间的最终关系,
(2.101)
称为场景辐射度L与到达像素传感器的光(辐照度)E之间的基本辐射关系,
(Horn 1986;Nalwa 1993;Ray 2002;Hecht 2015)。请注意,在这个公式中,光量取决于像素表面积(这也是为什么便携式相机的小传感器比单反相机(SLR)更嘈杂的原因),f数的平方倒数N = f/d(2.98),以及离轴衰减的四次方cos4 Q,这是自然暗角效应。
另一种主要的暗角类型称为机械暗角,由复式透镜中靠近边缘的透镜元件内部光线遮挡引起,不进行实际透镜设计的全光路追踪就难以用数学方法描述。然而,与自然暗角不同,通过减小相机光圈(增加f值)可以减少机械暗角。此外,还可以使用积分球、均匀照明目标或相机旋转等特殊设备对其进行校准(与自然暗角一起),具体讨论见第10.1.3节。
从一个或多个光源开始,光线反射一次或多次后穿过相机的光学系统(镜头),最终到达成像传感器。这些到达传感器的光子是如何转换成我们观察到的数字图像(红、绿、蓝)值的呢?在本节中,我们将建立一个简单的模型,以考虑最重要的效应,如曝光(增益和快门速度)、非线性映射、采样和混叠以及噪声。图2.23基于Healey和Kondepudy(1994)、Tsin、Ramesh和Kanade(2001)以及Liu、Szeliski等人(2008)开发的相机模型,展示了现代数码相机处理阶段的一个简化版本。Chakrabarti、Scharstein和Zickler(2009)开发了一个复杂的24参数模型,该模型更接近于数码相机中的实际处理过程,而Kim、Lin等人(2012)、Hasinoff、Sharlet等人(2016)以及Karaimer和Brown则进一步研究了这一领域。

图2.23图像传感管道,显示各种噪声源以及典型的数字后处理步骤。
(2016)提供了更现代的相机内处理流程模型。最近,布鲁克斯、米尔登霍尔等人(2019)开发了详细的相机内图像处理流程模型,用于将噪声JPEG图像反向(未处理)还原为其原始RAW格式,以便更好地去噪;而曾、余等人(2019)则开发了一种可调相机处理流程模型,可用于图像质量优化。
落在成像传感器上的光线通常由活动感应区域接收,在曝光期间集成(通常以秒的分数表示,例如,,感测放大器。目前数字静态和视频摄像机中使用的两种主要传感器是电荷耦合器
(CCD)和互补金属氧化物硅(CMOS)。
在CCD中,光子在曝光时间内会在每个活性阱中累积。然后,在传输阶段,电荷以一种“接力赛”的方式从一个阱转移到另一个阱,直到它们被沉积到感应放大器上,放大信号并传递给模数转换器(ADC)。较旧的CCD传感器容易发生溢出现象,即一个过度曝光像素的电荷会溢入相邻的像素,但大多数新型CCD都采用了防溢技术(即多余的电荷可以流入的“凹槽”)。

图2.24数字成像传感器:(a)CCD将光生电荷从一个像素移动到另一个像素,并在输出节点将其转换为电压;CMOS成像器则在每个像素内部将电荷转换为电压(Litwiller 2005)©2005光子学光谱;来自https://micro.magnet.fsu.edu/primer/digitalimaging/ cmosimagesensors.html的CMOS像素传感器剖面图。
光电探测器,可以选择性地进行门控以控制曝光时间,并在读出前通过多路复用方案局部放大。传统上,在质量敏感的应用中,如数码单反相机,CCD传感器的表现优于CMOS,而CMOS则更适合低功耗应用,但如今大多数数码相机都使用了CMOS。
影响数字图像传感器性能的主要因素包括快门速度、采样间距、填充因子、芯片尺寸、模拟增益、传感器噪声以及模数转换器的分辨率(和质量)。许多这些参数的实际值可以从嵌入数字图像中的EXIF标签读取,而其他参数则可以从相机制造商的规格表或相机评测和校准网站获取。
快门速度。快门速度(曝光时间)直接影响到达传感器的光线量,从而决定图像是否过曝或欠曝。(对于明亮场景,为了获得浅景深或运动模糊效果,摄影师有时会使用中性密度滤镜。)对于动态场景,快门速度还决定了最终照片中的运动模糊程度。通常,较高的快门速度(较少的运动模糊)会使后续分析更加容易(有关消除这种模糊的技术,请参见第10.3节)。然而,在录制视频以供显示时,为了避免频闪效应,可能需要一些运动模糊。
采样间距。采样间距是指成像芯片上相邻传感器单元之间的物理间隔(图2.24)。采样间距越小,传感器的采样密度越高,因此在给定的有源芯片面积内,分辨率(以像素计)更高。然而,较小的间距也意味着每个传感器的面积更小,无法积累足够的光子;这使得它对光线的敏感度降低,更容易产生噪声。
填充因子。填充因子是指实际感光区域大小与理论可用感光区域(水平和垂直采样间距的乘积)的比例。较高的填充因子通常更优,因为它们能捕捉更多的光线并减少混叠现象(见第tion2.3.1节)。虽然最初填充因子受限于需要在活动感光区域之间放置额外的电子元件,但现代背面照明(或背照式)传感器结合高效的微透镜设计,已大大消除了这一限制(Fontaine 2015)。相机的填充因子可以通过光度相机校准过程经验确定(见第10.1.4节)。
芯片尺寸。
),而数码单反相机则试图接近传统35毫米胶片画幅的大小。17当整体设备尺寸不重要时,较大的芯片尺寸更为理想,因为每个传感器单元可以更敏感地捕捉光线。(对于紧凑型相机而言,较小的芯片意味着所有光学元件都可以按比例缩小。)然而,更大的芯片生产成本更高,不仅因为每片晶圆中可容纳的芯片数量减少,还因为芯片缺陷的概率会随着芯片面积的增加呈指数级增长
模拟增益。在模数转换之前,通常会通过一个感知放大器来增强检测信号。在摄像机中,这些放大器的增益传统上由自动增益控制(AGC)逻辑控制,以调整这些值以获得良好的整体曝光。在较新的数码静态相机中,用户现在可以通过ISO设置对此增益进行额外控制,ISO通常以ISO标准单位表示,如100、200或400。由于大多数相机中的自动曝光控制也会调整
这些数字指的是旧摄像机中使用的视频管的“管径”。佳能SD800相机上的1/2.5英寸传感器实际上测量为5.76毫米×4.29毫米,即相当于35毫米全画幅(36毫米×24毫米)DSLR传感器尺寸的六分之一(在侧面)。
当DSLR芯片未能填满35毫米全画幅时,会对镜头焦距产生倍增效应。例如,一个只有35毫米画幅0.6倍大小的芯片,会使50毫米镜头的图像角范围与50/0.6 = 50×1.6=80毫米镜头相同,如公式(2.60)所示。
光圈和快门速度,手动设置ISO会从相机控制中移除一个自由度,就像手动指定光圈和快门速度一样。理论上,更高的增益可以让相机在低光条件下表现更好(当光圈已经最大时,长时间曝光可以减少运动模糊)。然而,在实际操作中,较高的ISO设置通常会放大传感器的噪点。
传感器噪声。在整个感知过程中,噪声来自各种来源,可能包括固定模式噪声、暗电流噪声、散粒噪声、放大器噪声和量化噪声(Healey和Kondepudy 1994;Tsin、Ramesh和Kanade 2001)。采样图像中最终存在的噪声量取决于所有这些因素,以及入射光(由场景辐射度和光圈控制)、曝光时间和传感器增益。此外,在低光照条件下,由于光子计数较低导致的噪声,泊松模型可能比高斯模型更合适(Alter、Matsushita和Tang 2006;Matsushita和Lin 2007a;Wilburn、Xu和Matsushita 2008;Takamatsu、Matsushita和Ikeuchi 2008)。
正如第10.1.1节中详细讨论的那样,Liu、Szeliski等人(2008)使用该模型,结合Grossberg和Nayar(2004)获得的相机响应函数(CRFs)的经验数据库,来估计给定图像的噪声水平函数(NLF),该函数预测了给定像素的整体噪声方差,作为其亮度的函数(每个颜色通道分别估计一个NLF)。另一种方法是在拍摄前访问相机,通过多次拍摄包含各种颜色和亮度的场景来预校准NLF,例如图10.3b所示的麦凯布色卡(McCamy、Marcus和Davidson 1976)。(在估计方差时,务必丢弃或降低梯度较大的像素权重,因为曝光之间的微小变化会影响这些像素的感知值。)不幸的是,由于传感系统内部发生的复杂相互作用,预校准过程可能需要针对不同的曝光时间和增益设置重复进行。
在实际应用中,大多数计算机视觉算法,如图像去噪、边缘检测和立体匹配,都至少需要一个初步的噪声水平估计。除了能够预先校准相机或对同一场景进行多次拍摄外,最简单的方法是寻找值接近常数的区域,并估计这些区域中的噪声方差(刘、斯泽利斯基等,2008)。
模拟分辨率。成像传感器内部模拟处理链的最后一步是模拟到数字转换(ADC)。虽然可以使用多种技术来实现这一过程,但两个重要的量是该过程的分辨率
(它产生的位数)和其噪声水平(这些位中有多少在实际应用中是有用的)。对于大多数相机而言,所引用的位数(压缩JPEG图像为8位,而某些单反相机提供的RAW格式则标称为16位)超过了实际可用的位数。判断的最佳方法是校准特定传感器的噪声,例如,通过拍摄同一场景的多次照片,并绘制估计噪声与亮度的关系图(练习2.6)。
数字后处理。一旦到达传感器的辐照度值被转换为数字位,大多数相机会执行多种数字信号处理(DSP)操作来增强图像,然后再压缩和存储像素值。这些操作包括彩色滤光阵列(CFA)去马赛克、白点设置以及通过伽玛函数映射亮度值以增加信号的感知动态范围。我们将在第2.3.2节中讨论这些主题,但在那之前,我们先回到与传感器阵列填充因子相关的混叠问题
新型成像传感器。成像传感器及相关技术如深度传感器的能力正在迅速发展。跟踪这些发展的会议包括由影像科学与技术学会赞助的电子影像科学与技术IS&T研讨会和影像传感器世界博客。
当一束光照射到图像传感器上,落在成像芯片的有源感应区域时会发生什么?到达每个有源单元的光子会被积分并数字化,如图2.24所示。然而,如果芯片上的填充因子较小且信号没有其他带限,可能会产生视觉上不悦的混叠现象。
为了探讨混叠现象,我们首先来看一个一维信号(图2.25),其中包含两个正弦波,一个频率为f = 3/4,另一个频率为f = 5/4。如果我们以f = 2的频率采样这两个信号,我们会发现它们产生了相同的样本(用黑色表示),因此我们说它们是混叠的。为什么这是一个不良效应?本质上,我们无法重建原始信号,因为我们不知道哪个原始频率存在。
事实上,Shannon的采样定理表明,重建信号所需的最小采样(Oppenheim和Schafer1996;Oppenheim、Schafer和Buck1999)速率

图2.25一维信号的混叠:当采样频率为f = 2时,频率为f = 3/4的蓝色正弦波和频率为f = 5/4的红色正弦波具有相同的数字样本。即使经过100%填充因子的矩形滤波器卷积后,这两个信号虽然不再具有相同的幅度,但仍然存在混叠现象,即采样的红色信号看起来像是蓝色信号的倒置低幅度版本。(右侧图像放大以提高可见度。实际正弦波的幅度分别为其原始值的30%和-18%。)
从其瞬时采样值必须至少是最高频率的两倍,19
fs ≥ 2fmax. (2.103)
信号中的最大频率称为奈奎斯特频率,最小采样频率的倒数rs = 1/fs称为奈奎斯特速率。
然而,你可能会问,由于成像芯片实际上是在有限区域内平均光场,那么点采样的结果是否仍然适用?在传感器区域内取平均值确实会减弱一些高频成分。但是,即使填充因子为100%,如图2.25右侧所示,高于奈奎斯特极限(采样频率的一半)的频率仍然会产生混叠信号,尽管其幅度小于相应的带限信号。
一个更令人信服的理由是,使用质量较差的滤波器(如方波滤波器)对信号进行降采样时,混叠效应会更加明显。图2.26展示了一个高频线性调频图像(之所以称为线性调频,是因为频率随时间增加),并显示了用25%填充因子面积传感器、100%填充因子传感器以及高质量9抽头滤波器对其进行采样的结果。关于降采样(抽取)滤波器的更多示例,可参见第3.5.2节和图3.29。
预测成像系统(甚至图像处理算法)产生的混叠量的最佳方法是估计点扩散函数(PSF),它表示特定像素传感器对理想点光源的响应。PSF是光学系统(透镜)引起的模糊与有限分辨率的组合(卷积)。

图2.26二维信号的混叠:(a)原始全分辨率图像;(b)使用25%填充因子的25倍下采样×滤波器;(c)使用100%填充因子的25倍下采样×滤波器;(d)使用高质量9抽头滤波器的25倍下采样×滤波器。请注意,使用低质量滤波器时,高频部分被混叠到可见频率中,而9抽头滤波器则完全去除了这些高频成分。
芯片传感器的集成区域。20
如果我们知道镜头的模糊函数以及成像芯片的填充因子(传感器面积形状和间距)(可选地,还包括抗混叠滤波器的响应),我们就可以将这些参数卷积(如第3.2节所述)以获得PSF。图2.27a显示了一个假设其模糊函数为半径等于像素间距s的圆盘的镜头的一维截面,该镜头的水平填充因子为80%。通过对这个PSF进行傅里叶变换(第3.4节),我们可以得到调制传递函数(MTF),从而估计混叠量,即傅里叶幅度在f≤fs奈奎斯特频率之外的区域。21如果我们将镜头失焦,使模糊函数的半径变为2s(图2.27c),我们会发现混叠量显著减少,但图像细节(接近f = fs的频率)也减少了。
在实验室条件下,可以通过观察一个点光源(如黑色纸板上的针孔)从后面照亮来估算PSF(精确到像素级别)。然而,这种PSF(即针孔的实际图像)仅能精确到像素分辨率,虽然它可以模拟较大的模糊(例如由失焦引起的模糊),但无法模拟PSF的亚像素形状并预测混叠的程度。另一种技术,如第10.1.4节所述,是观察校准图案(例如由倾斜的台阶边缘组成的图案(Reichenbach,Park和Narayanswamy 1991;Williams和Burns 2001;Joshi,Szeliski和

图2.27样本点扩散函数(PSF):(a)中模糊圆盘(蓝色)的直径等于像素间距的一半,而(c)中的直径是像素间距的两倍。感测芯片的水平填充因子为80%,以棕色显示。这两个核的卷积给出了点扩散函数,以绿色显示。PSF的傅里叶响应(MTF)在(b)和(d).中绘制。奈奎斯特频率以上的区域,即发生混叠的地方,用红色表示。
Kriegman2008))的理想外观可以重新合成到亚像素精度。
除了在图像采集过程中发生外,混叠现象还可能出现在各种图像处理操作中,如重采样、上采样和下采样。第3.4节和第3.5.2节讨论了这些问题,并展示了如何通过精心选择滤波器来减少混叠现象。
在第2.2节中,我们探讨了光照和表面反射如何随波长变化。当入射光照射到成像传感器时,来自光谱不同部分的光线以某种方式整合为我们在数字图像中看到的离散红、绿、蓝(RGB)颜色值。这一过程是如何运作的?我们又如何分析和操控这些颜色值?
你可能还记得童年时混合颜料颜色的神奇过程

图2.28原色和次色:(a)加法颜色红、绿、蓝可以混合产生青色、品红色、黄色和白色;(b)减法颜色青色、品红色和黄色可以混合产生红色、绿色、蓝色和黑色。
获取新的颜色。你可能记得,蓝色+黄色产生绿色,红色+蓝色产生紫色,红色+绿色产生棕色。如果你稍后重新学习这个主题,可能会了解到正确的减法三原色实际上是青色(浅蓝绿色)、品红(粉红色)和黄色(图2.28b),尽管黑色在四色印刷(CMYK)中也经常使用。如果你后来上过绘画课,就会学到颜色还有更奇特的名字,比如胭脂红、天蓝和黄油绿。减色颜料之所以称为减色,是因为颜料中的色素会吸收光谱中的某些波长。
稍后,您可能已经了解了加法原色(红色、绿色和蓝色),以及它们如何被添加(通过幻灯机或计算机显示器)来产生青色、品红、黄色、白色以及我们在电视机和显示器上通常看到的所有其他颜色(图2.28a)。
两种不同的颜色,比如红色和绿色,通过什么过程可以相互作用产生第三种颜色,比如黄色?波长是否以某种方式混合起来产生新的波长?
你可能知道,正确答案与物理混合波长无关。相反,三种原色的存在是由于人类视觉系统的三刺激(或三色)特性,因为我们有三种不同类型的细胞,称为视锥细胞,每种细胞对颜色光谱的不同部分都有选择性的反应(Glassner 1995;Wandell 1995;Wyszecki和Stiles 2000;Livingstone 2008;Frisby和Stone 2010;Reinhard,Heidrich等2010;Fairchild2013).23注意对于机器

图2.29标准CIE颜色匹配函数:(a) r-(λ),g-(λ),(λ)从纯色与R=700.0nm、G=546.1nm和B=435.8nm基色匹配得到的颜色光谱;(b) x-(λ),y-(λ),z-(λ)颜色匹配函数,它们是这些基色的线性组合。
(r-(λ),g-(λ),b(λ))光谱。
在诸如遥感和地形分类等应用中,最好使用更多的波长。同样,在近红外(NIR)范围内进行探测往往有利于监视应用。
CIE RGB和XYZ
为了测试和量化感知的三色理论,我们可以尝试将所有单色(单一波长)颜色作为三种适当选择的基色混合物来重现。(纯波长光可以通过棱镜或特制的颜色滤光片获得。)20世纪30年代,国际照明委员会(CIE)通过使用红(700.0纳米波长)、绿(546.1nm)和蓝(435.8nm)三种基色进行颜色匹配实验,标准化了RGB表示法。
图2.29展示了使用标准观察者进行这些实验的结果,即在大量受试者中平均感知结果。你会注意到,在蓝绿色范围内的某些纯色谱中,需要添加负数的红光量,也就是说,为了匹配颜色,需要向被匹配的颜色中加入一定量的红色。这些结果还提供了一个简单的解释,说明了同色异谱现象的存在,即具有不同光谱但感知上无法区分的颜色。请注意,两种在特定光源下是同色异谱的织物或颜料颜色,在不同的光照条件下可能不再如此。
由于混合负光的问题,CIE也开发了一种
正如Michael Brown在他的颜色教程中指出的那样(Brown2019),标准观察者实际上只是在20世纪20年代对17名英国受试者进行的平均测量。
新的颜色空间称为XYZ,其中包含其正八分之一中所有的纯光谱颜色。(它还将Y轴映射到亮度,即感知相对亮度,并将纯白色映射到一个对角线(等值)向量。)从RGB到XYZ的转换由下式给出
(2.104)虽然CIE XYZ标准的官方定义将矩阵标准化,使得纯红色对应的Y值为1,但更常用的形式是省略前导分数,使得第二行加起来等于1,即RGB三元组(1,1,1)对应一个Y值。
根据公式(2.104),将图2.29a中的(r-(λ),g-(λ),(λ))曲线线性混合,得到图2.29b所示的(x-(λ),y-(λ),z-(λ))曲线。请注意,现在所有三个光谱(颜色匹配函数)都只有正值,且y-(λ)曲线与人类感知的亮度相吻合。
如果我们将XYZ值除以X+Y+Z的总和,我们得到色度坐标
(2.105)
它们之和为1。色度坐标忽略了给定颜色样本的绝对强度,仅表示其纯色。如果我们从图2.29b中的单色参数λ = 380nm到λ = 800nm扫动,就会得到图2.30a所示的熟悉色度图。该图显示了大多数人类可感知的所有颜色值的(x,y)坐标。(当然,本书中的CMYK再现过程实际上并未覆盖所有可感知的颜色范围。)外部弯曲边缘表示所有纯单色值在(x,y)空间中的映射位置,而连接两个端点的下直线称为紫线。插图中的三角形表示原始颜色匹配实验中使用的红、绿、蓝单波长基色,而E表示白点。
因此,当我们想要将亮度和色度分开时,颜色值的方便表示是Yxy(亮度加上两个最独特的色度分量)。
虽然XYZ颜色空间具有许多方便的特性,包括能够将亮度与色度分开,但它实际上并不能预测人类感知颜色或亮度差异的能力。

图2.30 CIE色度图,显示了沿边缘的纯单波长光谱颜色以及E处的白点,按其对应的(x,y)值绘制。(a)红色、绿色和蓝色原色未能覆盖整个色域,因此需要添加负数的红色来覆盖蓝绿范围;(b)麦克亚当椭圆
显示具有相同辨别能力的颜色区域,并构成Lab感知颜色空间的基础。
由于人类视觉系统的响应大致呈对数关系(我们能够感知到大约1%的相对亮度差异),CIE定义了XYZ空间的非线性重新映射,称为L*a*b*(有时也称为CIELAB),其中亮度或色度的差异在感知上更加均匀,如图2.30b.25所示。
亮度的L*分量定义为
(2.106)
其中Yn是标称白光的亮度值(Fairchild2013)
(2.107)
同时开发并标准化了另一种感知驱动色彩空间,称为L*u*v*(Fairchild2013)。
同样地,a*和b*分量定义为
2.108)
其中,(Xn、Yn、Zn)是测量的白点。图2.33i-k显示了样本彩色图像的L*a*b*表示法。
虽然前面的讨论告诉我们如何唯一地描述任何颜色(光谱分布)的感知三刺激描述,但它并没有解释RGB静态和视频摄像机实际上是如何工作的。它们是否只是测量红(700.0nm)、绿(546.1nm)和蓝(435.8nm)的名义波长下的光量?彩色显示器是否只是发出这些特定波长的光,如果是这样,它们又是如何发出负红色光来再现青色范围内的颜色呢?
事实上,RGB摄像机的设计历来基于电视中使用的彩色荧光粉的可用性。当标准清晰度彩色电视发明时(NTSC),定义了驱动阴极射线管(CRT)中的三个颜色枪的RGB值与明确定义感知颜色的XYZ值之间的映射关系(这一标准被称为ITU-R BT.601)。随着高清电视和新型显示器的出现,创建了一个新的标准,即ITU-R BT.709,该标准规定了每种颜色基色的XYZ值,
(2.109)
在实践中,每个彩色相机根据其红、绿、蓝传感器的光谱响应函数来整合光线,
R = ∫ L(λ)SR (λ)dλ,
G = ∫ L(λ)SG (λ)dλ, (2.110)
B = ∫ L(λ)SB (λ)dλ,
其中L(λ)是给定像素处的入射光谱,{SR (λ),SG (λ),SB (λ)}是相应传感器的红、绿、蓝光谱灵敏度。
我们能知道相机实际的光谱敏感度吗?除非相机制造商提供这些数据,或者我们观察到相机对整个单色光谱的响应,否则这些敏感度不会被像BT.709这样的标准所规定。相反,重要的是给定颜色的三刺激值能够产生指定的RGB值。制造商可以自由使用与标准XYZ定义不匹配的传感器,只要它们之后可以通过线性变换转换为标准颜色即可。
同样地,虽然电视和电脑显示器应该按照公式(2.109)生成RGB值,但没有理由不能使用数字逻辑将接收到的RGB值转换成不同的信号来驱动每个颜色通道。26校准良好的显示器可以将这些信息提供给执行色彩管理的软件应用,从而使现实中的颜色、屏幕上的颜色以及打印机上的颜色尽可能地匹配。
早期彩色电视摄像机使用三个视像管(电子管)进行感光,后来的摄像机使用三个独立的RGB感光芯片,而当今大多数数字静态和视频摄像机使用彩色滤光阵列(CFA),其中交替的传感器被不同颜色的滤光片覆盖(图2.24)。27
当今彩色相机中最常用的图案是拜耳模式(Bayer 1976),该模式在传感器的一半上放置绿色滤镜(以棋盘格形式排列),其余部分则放置红色和蓝色滤镜(图2.31)。绿色滤镜的数量是红色和蓝色滤镜的两倍,这是因为亮度信号主要由绿色值决定,而视觉系统对亮度中的高频细节比色度更为敏感(这一事实被用于彩色图像压缩——见第2.3.3节)。通过插值缺失的颜色值,使所有像素都有有效的RGB值的过程称为去马赛克,详细内容见第10.3.1节。
同样,彩色液晶显示器通常使用交替排列的红、绿、蓝滤光片,置于每个液晶活动区域前,以模拟全彩显示的效果。由于视觉系统在亮度分辨率(清晰度)上高于色度分辨率,因此可以对RGB(及单色)图像进行数字预滤波,以增强

图2.31拜耳RGB模式:(a)彩色滤光片阵列布局;(b)插值像素值,
未知(猜测)值显示为小写。
脆度的感知(Betrisey,Blinn等人,2000;Platt2000b)。
在编码感知到的RGB值之前,大多数相机会执行某种颜色平衡操作,试图将给定图像的白点移得更接近纯白色(即RGB值相等)。如果色彩系统和照明条件相同(例如BT.709系统使用日光光源D65作为参考白),这种变化可能很小。然而,如果光源颜色强烈,如室内白炽灯(通常会导致黄色或橙色调),补偿可能会相当显著。
一种简单的颜色校正方法是将每个RGB值乘以不同的因子(即,在RGB色彩空间中应用对角矩阵变换)。更复杂的变换有时是通过映射到XYZ空间再返回实现的,实际上执行的是颜色扭曲,即使用一个通用的3×3颜色变换矩阵。练习2.8让你探索这些问题。
在黑白电视的早期,用于显示电视信号的CRT中的荧光粉对输入电压的响应是非线性的。电压与最终亮度之间的关系由一个称为gamma(√)的数字来表征,因为公式大致为
B = V ; (2.111)
你们中那些还记得彩色电视早期的人自然会想到电视机上的色调调节旋钮,它可以产生真正奇怪的结果。

图2.32伽玛压缩:(a)输入信号亮度Y与传输信号Y之间的关系由Y,=Y 1/给出。(b)在接收器中,信号Y,
乘以因子√,=Y。传输过程中引入的噪声被压缩
在黑暗区域,这对应于视觉系统中更敏感的噪声区域。
√约为2.2。为了补偿这种影响,电视摄像机中的电子设备将通过逆伽玛预映射感知亮度Y,
Y, = Y ;
(2.112)
典型值为1 = 0.45。
信号在传输前通过这种非线性映射有一个有益的副作用:传输过程中增加的噪声(记住,那是模拟时代!)会在信号较暗的部分减少(在接收端应用伽马函数后),这些部分的噪声更为明显(图2.32)。29(记住,我们的视觉系统大致对亮度的相对差异敏感。)
当彩色电视发明时,决定将红、绿、蓝信号分别通过相同的伽马非线性处理,然后再合并进行编码。如今,尽管我们的传输系统中不再有模拟噪声,但在压缩过程中信号仍然会被量化(见第2.3.3节),因此对感知值应用逆伽马仍然有用。
不幸的是,对于计算机视觉和计算机图形学而言,图像中伽马的存在常常是一个问题。例如,正确模拟辐射现象如阴影(见第2.2节和公式(2.88))发生在线性辐射空间中。一旦所有计算完成,在显示前应应用适当的伽马值。然而,许多计算机图形系统(如着色模型)运行时
直接使用RGB值并直接显示这些值。(幸运的是,较新的彩色成像标准,如16位scRGB使用线性空间,这使得这个问题不那么严重(Glassner1995)。)
在计算机视觉中,情况可能会更加严峻。准确确定表面法线,使用光度立体技术(第13.1.1节)或更简单的操作如精确图像去模糊,都需要测量值处于强度的线性空间中。因此,在进行这些详细的定量计算时,首先需要消除感知颜色值中的伽马和每幅图像的颜色重新平衡。查克拉巴蒂、沙尔斯坦和齐克勒(2009)开发了一个复杂的24参数模型,该模型与当今数字相机的处理过程非常匹配;他们还提供了一个颜色图像数据库,供您自行测试使用。
对于其他视觉应用,例如特征检测或立体信号匹配和运动估计,这种线性化步骤通常不是必需的。事实上,判断是否需要反向处理伽马值可能需要仔细思考,例如,在图像拼接中补偿曝光变化的情况(见练习2.7)。
如果所有这些处理步骤对模型来说听起来很混乱,那确实如此。练习2.9要求你尝试通过经验研究来区分其中的一些现象,即拍摄彩色图表的照片并比较RAW和JPEG压缩后的颜色值。
其他色彩空间
虽然RGB和XYZ是用于描述颜色信号的光谱内容(因此,三刺激响应)的主要颜色空间,但在视频和静止图像编码以及计算机图形中已经开发了各种其他表示。
最早的用于视频传输的颜色表示是为北美NTSC视频开发的YIQ标准,以及为欧洲PAL开发的密切相关YUV标准。在这两种情况下,都希望有一个亮度通道Y(之所以这样命名是因为它仅大致模拟真实的亮度),使其与常规黑白电视信号相当,同时还有两个较低频率的色度通道。
在这两个系统中,Y信号(或者更准确地说,Y‘亮度信号,因为它经过了伽马压缩)是从以下获得的:
Y6,01 = 0.299R, + 0.587G, + 0.114B, , (2.113)
其中,R、G、B是伽玛压缩颜色分量的三元组。当使用BT.709中HDTV的新颜色定义时,公式为
Y7,09 = 0.2125R, + 0.7154G, + 0.0721B,. (2.114)
(B’-Y’)和(R’-Y’)的缩放版本,即U=0.492111(B’-Y’)和V=0.877283(R’-Y’), (2.115)
而IQ分量是UV分量旋转了33°的角度。在复合(NTSC和PAL)视频中,色度信号先经过水平低通滤波,然后调制并叠加在Y‘亮度信号上。为了实现向后兼容,旧的黑白电视机要么忽略高频色度信号(因为电子设备较慢),或者最坏的情况是在主信号上叠加一个高频图案。
虽然这些转换在计算机视觉早期非常重要,当时帧采集器会直接将复合电视信号数字化,但如今所有数字视频和静态图像压缩标准都基于较新的YCbCr转换。YCbCr与YUV密切相关(Cb和Cr信号携带蓝红色差信号,比UV更有用的助记符),但使用不同的比例因子以适应数字信号可用的八位范围。
对于视频,Y信号被重新缩放以适应[16... 235]的值范围,而Cb和Cr信号则被缩放到[16... 240](Gomes和Velho 1997;Fairchild 2013)。对于静态图像,JPEG标准使用完整的八位范围,没有保留值,
其中,R‘G’B‘值是八位伽马压缩的颜色分量(即我们打开或显示JPEG图像时实际获得的RGB值)。对于大多数应用而言,这个公式并不那么重要,因为你的图像读取软件会直接提供八位伽马压缩的R’G‘B’值。然而,如果你尝试进行精细的图像去块处理(练习4.3),这些信息可能会很有用。
你可能会遇到另一种颜色空间,即色相、饱和度、亮度(HSV),这是RGB颜色立方体投影到非线性色度角度、径向饱和百分比和受亮度启发的值上的结果。具体来说,亮度定义为平均或最大颜色值,饱和度定义为与对角线的距离比例,而色相则定义为围绕色轮的方向(确切公式由Hall(1989)、Hughes、van Dam等人(2013)和Brown(2019)描述)。这种分解在图形应用中非常自然,例如颜色选择(它近似于穆塞尔色卡的颜色描述)。图2.33l-n展示了样本彩色图像的HSV表示,
如果您希望您的计算机视觉算法只影响图像的值(亮度),而不影响其饱和度或色调,一个更简单的解决方案是使用定义在(2.105)中的Y xy(亮度+色度)坐标或更简单的颜色比率,
(2.117)
(图2.33e-h)。在对亮度(2.113)进行处理后,例如通过直方图均衡化过程(第3.1.4节),您可以将每个颜色比率乘以新亮度与旧亮度的比率,以获得调整后的RGB三元组。
虽然所有这些颜色系统听起来可能令人困惑,但最终你选择哪一个其实并不那么重要。Poynton在他的《颜色常见问题》https://www.poynton.com/ ColorFAQ.html中指出,感知驱动的L*a*b*系统在定性上与我们主要使用的伽马压缩R‘G’B‘系统相似,因为两者都具有分数幂缩放(近似对数响应)特性,即实际强度值与被处理的数字之间存在这种关系。正如所有情况一样,在决定使用哪种技术之前,请仔细考虑你的目标是什么。
相机处理管道的最后一个阶段通常是某种形式的图像压缩(除非您使用的是无损压缩方案,如camera RAW或PNG)。
所有彩色视频和图像压缩算法首先将信号转换为YCbCr(或某些密切相关的变体),以便能够以更高的保真度压缩亮度信号,而不是色度信号。(记住,人眼对颜色变化的频率响应不如对亮度变化的频率响应。)在视频中,通常会将Cb和Cr水平方向上以二分之一的比例抽样;对于静态图像(如JPEG),抽样(平均)则同时发生在水平和垂直方向。
一旦亮度和色度图像被适当地子采样并分离成单独的图像,它们就会传递到块变换阶段。这里最常用的技术是离散余弦变换(DCT),这是离散傅里叶变换(DFT)的一个实值变体(见第3.4.1节)。DCT是对自然图像块的卡鲁恩-洛夫或特征值分解的一种合理近似,即同时将最大能量打包到前几个系数中,并对像素之间的联合协方差矩阵进行对角化(使变换系数在统计上独立)。MPEG和JPEG都使用8×8 DCT变换(Wallace1991;

图2.33色彩空间转换:(a-d)RGB;(e-h)rgb。(i-k)L*a*b*;(l-n)HSV。注意,RGB、L*a*b*和HSV值都重新调整以适应打印页面的动态范围。

块伪影和高频混叠(“蚊子噪声”)从左到右增加。
尽管有更新的变体,包括新的AV1开放标准,30使用更小的4×4甚至2×2块。替代变换,如小波(Taubman和Marcellin2002)和重叠变换(Malvar1990,1998,2000)被用于JPEG 2000和JPEG XR等压缩标准中。
变换编码后,系数值被量化为一组小整数值,这些值可以使用可变比特长度方案进行编码,例如霍夫曼码或算术码(Wallace1991;Marpe、Schwarz和Wiegand2003)。(直流(最低频率)系数也从前一个块的直流值自适应预测。术语“DC”来源于“直流”,即信号的非正弦或非交变部分。)量化中的步长是主要变量,由JPEG文件的质量设置控制(图2.34)。
使用视频时,通常还会执行基于块的运动补偿,即编码每个块与前一帧中移位块预测出的一组像素值之间的差异。(例外情况是旧款数字摄像机中使用的运动JPEG方案,这不过是一系列单独的JPEG压缩图像帧。)虽然基本的MPEG使用16×16的运动补偿块和整数运动值(Le Gall 1991),但新标准采用了自适应大小的块、亚像素运动以及引用旧帧中的块的能力(Sullivan,Ohm等2012)。为了更优雅地从故障中恢复并允许对视频流进行随机访问,预测的P帧被穿插在独立编码的I帧之间。(双向B帧有时也会使用。)
压缩算法的质量通常使用其峰值信噪比(PSNR)来报告,该信噪比是从平均均方误差得出的,
其中,I(x)是原始未压缩图像,(x)是其压缩对应物,或者等效地,均方根误差(RMS误差),定义为
(2.119)
(2.120)
其中,Imax是最大信号范围,例如,对于8位图像,Imax为255。
虽然这只是图像压缩工作原理的一个高层次概述,但了解这一点有助于在各种计算机视觉应用中补偿由这些技术引入的伪影。此外,研究人员目前正在开发基于深度神经网络的新颖图像和视频压缩算法,例如(Rippel和Bourdev 2017;Mentzer、Agustsson等2019;Rippel、Nair等2019)以及https://www. compression.cc。这些技术会产生哪些不同类型的伪影,将是一件有趣的事情。
正如我们在本章开头提到的,本书只是对传统上在多个独立领域中所涵盖的一系列丰富而深入的主题进行的简要概述。
关于点、线、面和投影的几何更深入的介绍可以在多视图几何(Faugeras和Luong 2001;Hartley和Zisserman 2004)以及计算机图形学(Watt 1995;OpenGL-ARB 1997;Hughes,van Dam等2013;Marschner和Shirley 2015)的教科书中找到。更深入的主题包括高阶基元,如二次曲面、圆锥曲线和三次曲线,以及三视图和多视图几何。
图像形成(合成)过程传统上作为计算机图形学课程的一部分进行教学(Glassner1995;Watt1995;Hughes,van Dam等2013;Marschner和Shirley 2015),但在基于物理的计算机视觉中也有研究(Wolff,Shafer和Healey 1992a)。相机镜头系统的特性在光学领域也有探讨(Mo...ller1988;Ray 2002;Hecht2015)。
关于色彩理论的一些好书包括:希利和沙弗(1992)、万德尔(1995)、维斯切基和斯蒂尔斯(2000)以及费尔柴尔德(2013)。利文斯通(2008)则提供了一种更有趣且非正式的色彩感知入门。马克·费尔柴尔德的色彩书籍和链接页面列出了许多其他资源。
与采样和混叠有关的主题在信号和图像处理教科书中都有介绍(Crane1997;Ja...hne1997;Oppenheim和Schafer1996;Oppenheim、Schafer和Buck 1999;Pratt 2007;Russ 2007;Burger和Burge2008;Gonzalez和Woods2017)。
两门课程详细地涵盖了上述许多主题(图像形成、镜头、色彩和采样理论),分别是斯坦福大学的马克·莱沃伊的《数字摄影》课程(Levoy2010)和迈克尔·布朗在2019年国际计算机视觉会议上的图像处理流水线教程(Brown2019)。最近,池内、松下等人(2020)出版的一本书也涉及了三维几何、光度测量和传感器模型,但重点放在主动照明系统上。
给学生的提示:本章练习较少,因为内容主要集中在背景知识上,实用技巧不多。如果你希望深入理解多视图几何,我建议你阅读并完成哈特利和齐瑟曼(2004)提供的练习。同样,如果你想了解与图像形成过程相关的练习,格拉斯纳(1995)的书充满了挑战性的问题。
例2.1:最小二乘法交点和直线拟合-高级。方程(2.4)显示了如何将两条二维线的交点表示为它们的叉积,假设
线用齐次坐标表示。
与每条线的平方距离,
(2.121)
将量平方化为二次形式,TA~x。)
2.为了将一条直线拟合到一组点上,可以计算这些点的质心(平均值)以及围绕该平均值的点的协方差矩阵。证明通过质心并沿着协方差椭球的主要轴(最大特征向量)的直线,能够最小化到各点的距离平方和。
3.这两种方法本质上是不同的,尽管射影对偶告诉我们点和线是可以互换的。为什么这两种算法看起来如此不同?它们实际上是在最小化不同的目标吗?
例2.2:二维变换编辑器。编写一个程序,让你可以交互式地创建一组矩形,然后修改它们的“姿态”(二维变换)。你应该实现以下步骤:
1.打开一个空白窗口(“画布”)。
2.拖动(橡皮筋)以创建新矩形。
3.选择变形模式(运动模型):平移、刚性、相似性、仿射或透视。
4.拖动轮廓的任意一角,以更改其变换。
这个练习应该建立在一组像素坐标和变换类的基础上,这些类可以由你自己实现,也可以从软件库中获取。还应该支持创建的表示的持久性(保存和加载)(对于每个矩形,保存其变换)。
例2.3:3D查看器。编写一个简单的3D点、线和多边形查看器。导入一组点和线命令(基元)以及视图变换。交互式修改对象或相机变换。此查看器可以是您在练习2.2中创建的查看器的扩展。只需将视图变换替换为它们的3D对应物即可。
(可选)添加一个z-buffer以对多边形进行隐藏表面消除。(可选)使用3D绘图包并仅编写查看器控件。
例2.4:焦距和景深。找出镜头上的焦距和景深指示器是如何确定的。
1.计算并绘制焦距为Δzi的镜头(例如,焦距为100毫米)的焦点距离zo随行程距离的变化关系。这是否解释了你在典型镜头上看到的焦点距离呈双曲线变化的现象(图2.20)?
2.计算给定焦距设置zo的景深(最小和最大对焦距离),作为模糊圆直径c(使其成为传感器宽度的一部分)、焦距f和光圈值N(与光圈直径d相关)的函数。这是否解释了镜头上常见的景深标记,这些标记包围了对焦标记,如图2.20a所示?
3.现在考虑一个焦距变化的变焦镜头。假设在变焦过程中,镜头保持对焦,即后节点到传感器平面的距离zi自动调整以固定对焦距离zo。景深指示器随焦距的变化如何变化?你能重现图2.20b中镜头上看到的弯曲景深线的二维图吗?
例2.5:光圈值和快门速度。列出你的相机提供的常见光圈值和快门速度。在较旧的单反相机上,这些信息显示在镜头和快门速度拨盘上。在较新的相机上,你需要通过电子取景器(或液晶屏/指示器)手动调整曝光时查看这些信息。
1.这些是否形成几何级数?如果是,它们的比值是多少?这些与曝光值(EV)有何关系?
两倍,还是相差125/60 = 2.083?
3.你认为这些数字有多准确?你能设计出一种方法来精确测量光圈如何影响到达传感器的光线以及实际的曝光时间吗?
例2.6:噪声水平校准。通过将相机安装在三脚架上,多次拍摄同一场景来估算相机中的噪声量。(如果你拥有DSLR,购买一个遥控快门释放器是个不错的投资。)或者,拍摄一个颜色区域恒定的场景(如色卡),通过拟合每个颜色区域的平滑函数并计算与预测函数的差异来估算方差。
1.将每个颜色通道的估计方差作为级别函数绘制出来。
2.改变相机的ISO设置;如果不能这样做,减少场景中的整体光线(关掉灯光,拉上窗帘,等到黄昏)。噪声量是否随着ISO/增益而变化很大?
3.将你的相机与另一个不同价位或年份的相机进行比较。是否有证据表明“你付出了多少,就得到了多少”?数码相机的质量是否随着时间的推移而提高?
例2.7:图像拼接中的伽马校正。这是一个相对简单的谜题。假设你有两个图像,它们是全景图的一部分,你希望将它们拼接在一起(见第8.2节)。这两个图像是在不同的曝光条件下拍摄的,因此你需要调整RGB值,使它们在接缝处匹配。为了达到这个目的,是否需要先取消颜色值中的伽马校正?
例2.8:白点平衡——很棘手。执行白点调整的常见(在相机内或后处理)技术是拍摄一张白色纸张的照片,然后调整图像的RGB值,使其成为中性颜色。
1.描述如何根据样本“白色”(Rw;Gw;Bw)调整图像中的RGB值,使该颜色变为中性(不改变曝光)。
2.您的转换是否涉及对RGB值的简单(每个通道)缩放,还是需要一个完整的3×3颜色扭曲矩阵(或其他什么)?
3.将你的RGB值转换为XYZ。现在适当的校正是否仅依赖于XY(或xy)值?如果是这样,当你转换回RGB空间时,是否需要一个完整的3×3颜色扭曲矩阵来达到相同的效果?
4.如果你在直接RGB模式下使用纯对角线缩放,但在XYZ空间中工作时却出现了扭曲,你如何解释这种明显的二元性?哪种方法是正确的?(或者这两种方法都不正确吗?)
如果你想了解你的相机到底能做什么,请继续下一个练习。
例2.9:相机内色彩处理——具有挑战性。如果您的相机支持RAW像素模式,那么拍摄一对RAW和JPEG图像,看看您是否能够推断出当相机将RAW像素值转换为最终的、经过颜色校正和伽马压缩的八位JPEG像素值时所做的事情。
1.从共定位的RAW像素值和颜色映射像素值之间的对应关系中推断出颜色滤波器阵列的模式。如果这能让你的工作更轻松,可以使用色卡。你可能会发现将RAW图像分成四个独立的图像(偶数列和行与奇数列和行进行采样)并将其视为“虚拟”传感器会有所帮助。
2.通过拍摄包含强烈色彩边缘的具有挑战性的场景(如第10.3.1节所示)来评估去马赛克算法的质量。
3.如果在改变相机的色彩平衡值后,仍能拍出完全相同的照片,请比较这些设置对处理的影响。
4.将您的结果与(Chakrabarti、Scharstein和Zickler 2009)、Kim、Lin et al.(2012)、Hasinoff、Sharlet et al.(2016)、Karaimer和Brown中所列的结果进行比较
(2016),以及Brooks,Mildenhall等人(2019)或使用其彩色图像数据库中的可用数据。


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








