图（一）

1.概念

1.1一些定义

• 图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为G(V,E)，G表示一个图，V是图中顶点的集合，E是图G中边的集合。注：线性表中的数据叫元素；树中叫结点；图中称为顶点(Vertex)。线性表中可以没有元素，树中可以没有结点，但图中不能没有顶点，可以没有边。
• 无向边：顶点Vi和Vj之间的边没有方向，成这条边为无向边，用(Vi,Vj)表示。
• 无向图：图中任意两个顶点的边都是无向边。
• 有向边：若从顶点Vi到Vj的边有方向，则称这条边为有向边，也成为弧(Arc)，用<Vi,Vj>表示，其中Vi为弧尾，Vj为弧头。
• 有向图：图中任意两个顶点的边都是有向边。
• 简单图：不存在指向自身的边和重合的边的图。

• 无向完全图：无向图中，任意两个顶点之间都存在边。

• 有向完全图：有向图中，任意两个顶点之间都存在方向相反的两条弧。

• 稀疏图；有很少条边或弧的图称为稀疏图，反之称为稠密图。

• 权（Weight）：表示从图中一个顶点到另一个顶点的距离或耗费。

• 网：带有权重的图。

• 度：与特定顶点相连接的边数。

• 出度、入度：有向图中的概念，出度表示以此顶点为起点的边的数目，入度表示以此顶点为终点的边的数目。

• 环：第一个顶点和最后一个顶点相同的路径。

• 简单环：除去第一个顶点和最后一个顶点后没有重复顶点的环。

• 连通图：任意两个顶点都相互连通的图。

1.2图的分类

根据边是否有方向，图分为有向图和无向图。

无向图是指图中所有的边都不区分方向，如下图所示

图中顶点V1={A,B,C,D,E,F}

边E1={(A,B),(A,C),(B,C),(B,E),(B,F),(C,F),(C,D),(E,F),(C,E)}

有向图是指边带有方向，从弧尾指向弧头，如下图所示

2.图的存储结构

由于图的不同顶点的度数不同，若按照最大度数设计结点结构会造成存储浪费；如果按照顶点自己的度数设计不同结构，又会导致操作不便。

2.1邻接矩阵

邻接矩阵使用两个数组存储图的信息，其中一个一维数组存储顶点，另一个二维数组存储边的信息

如上图所示，数组中对角线元素为0，因此不存在顶点到自身的边。某行元素之和代表该顶点的出度，列元素之和代表入度。

如果是带有权值的网，二维数组中不在用0和1表示，而是把元素值表示为权值，不存在的边表示为无穷，对角线上的元素依然是0。

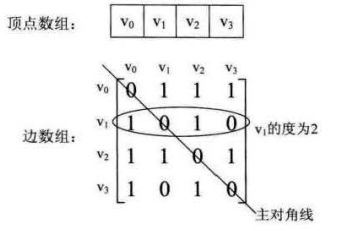
邻接矩阵定义的图比较方便，直接根据顶点个数定义相应大小的二维数组，再根据边的关系填充数据即可。对于无向图，邻接矩阵是个对称矩阵，因此实际上会有一定的空间浪费。

2.2邻接表

由于邻接矩阵造成了空间浪费，因此引入邻接表的概念，即用链表存储边的信息

如上图，数组用于存储顶点信息，其附带一个指针域指向第一个边，边的数据域存放了顶点在数组中的下表位置，指针域指向下一个边结点。连接表显示了顶点的出度信息，但需要遍历整个图才能知道出度信息。

2.3十字链表

十字链表将邻接表和逆邻接表相结合，解决了邻接表的缺陷

如上图，顶点结构中包含数据域、指向出边表的指针以及指向出边表的指针。边结构中第一个元素为边的起点在数组中的下标，第二个元素为边的终点在顶点数组中的下标，第三个元素指向入边表指针域，第四个元素指向出边表的下一边。

3.图的遍历

从图中国某一个顶点出发遍历其余顶点，每个顶点仅被访问一次。

3.1深度优先遍历

相当于一条路走到黑，发现多个出度时，首先选择右手边的边前进，当发现出度之后的顶点被访问过时，则回退一步继续搜查，发现没有访问过的顶点时继续前进，否则继续后退，直到所有顶点都被访问为止，以下图为例子

（1）从A出发，发现出度为B，F。选择右手边的B。A->B
（2）从B出发，出度为C,I,G，选择右手边的C
（3）从C出发，出度为I,D，选择右手边的D
（4）从D出发，出度为I,G,H,E，选择右手边的E
（5）从E出发，出度为H,F，选择右手边的F
（6）从F出发，出度为A,G，选择右手边的A，但发现A已经被遍历过，所以选择G
（7）从G出发，出度为B,D,H，B,D访问过了，选择H
（8）从H出发，出度为D,F，均被访问过了。但此时图中的节点并没有遍历完全，因此我们要按原路返回，去找没走过的路
（9）回退到G，发现所连接的BDFH均被访问；
（10）回退到F，没有通道；回退到E，没有通道，回退到D，发现一个点I，进行标记(若此时与D相邻的还有其他顶点，则在此时一起进行标记)；然后继续回退到A，走完整个路

int visited[MAXVEX] = {0};
void DFS(MGraphy g,int i){
    visited[i] = 1;
    printf("%c,\t",g.vexs[i]);
    for (int j = 0; j < g.vnum; j++) {
        if(g.arc[i][j]!=0 && g.arc[i][j]!=IUNFINITY && !visited[j]){
            DFS(g,j);
        }
    }
}
void DFSTraverse(MGraphy g){
    printf("deep first search begin.\n");
    for (int i = 0; i < g.vnum; i++) {
        if(!visited[i]){
            DFS(g,i);
        }
    }
}

int main() {
    MGraphy g ;
    createGraphy(&g);
    printf("graphy create success ! ! !\n");
    DFSTraverse(g);
}

3.2广度优先遍历

需要使用队列进行辅助，思路是每发现一个顶点后将其入队，将其设置为已经访问的标志后出队，找到和其相连的所有顶点并入队，再出队第一个位置的元素，如此往复。

void BFSTraverse(MGraphy g){
    SeqQueue *queue;
    initQueue(queue);   // 顺序表实现的队列，先初始化
    int visited[] = {0};    // 初始化每个结点对应为未访问
    int a;
    for(int i=0;i<g.vnum;i++){   // 对每个结点进行深度遍历
        if(visited[i] == 0){
            visited[i] = 1;
            printf("%c",g.vexs[i]);  // 深度遍历后对结点进行打印操作
            enQueue(queue,i);        // 将节点放到队列中
            while (queueLength(queue)){
                deQueue(queue,&a); // 取出对头元素，进行广度遍历
                for (int j = 0; j < g.vnum; ++j) {
                    if(g.arc[a][j] == 1 && visited[j]==0){   // 存在边，且对应的店没有方问过
                        visited[j] = 1;
                        printf("%c",g.vexs[j]);
                        enQueue(queue,j);                           // 遍历后再入队
                    }
                }
            }
        }
    }
}