栈

栈作为一种受限的线性表，同样可以划分为顺序结构存储的栈（这里简称顺序栈）和链式结构存储的栈（这里简称链栈）。

一.顺序栈

1.1定义

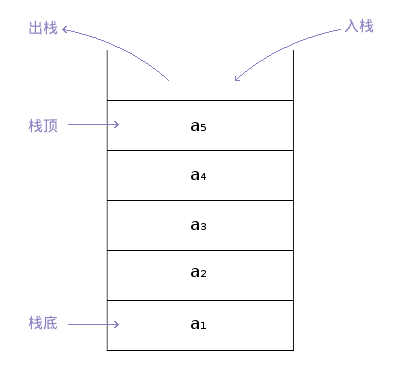
栈的顺序存储称为顺序栈，是利用一组地址连续的存储单元存放从栈底到栈顶的元素，同时附设一个指针（top）指示当前栈顶的位置。如图所示：

栈的顺序存储类型则可以描述为：

typedef struct{
    ElemType data[MaxSize];
    int top;
}SqStack;
 
 
1
2
3
4

这里对顺序栈的判断条件进行说明。

• 栈空条件：top==-1
• 栈满条件：top==MaxSize-1
• 栈长：top+1

1.2基本操作

1.2.1初始化操作

完成对栈顶指针的复位操作。

void InitStack(SqStack* s)
{
    s->top=-1;
}
 
 
1
2
3
4

1.2.2判空操作

如果栈为空，则返回0；如果栈不为空，则返回-1。

int StackEmpty(SqStack* s)
{
    if(s->top==-1){
        return 0;
    }else{
        return -1;
    }
}
 
 
1
2
3
4
5
6
7
8

1.2.3入栈操作

首先判断栈是否已满，如果栈已经满了，则返回-1；如若没有满，则在栈顶中插入元素，并返回0。

int Push(SqStack* s, ElemType x)
{
    if(s->top==MaxSize-1){
        return -1;
    }
    s->data[++s->top]=x;
    return 0;
}
 
 
1
2
3
4
5
6
7
8

1.2.4出栈操作

首先判断栈是否为空，如果已经为空，则返回-1；如果不为 空，则取得栈顶元素，并返回0。

int Pop(SqStack* s, ElemType* x)
{
    if(s->top==-1){
        return -1;
    }
    *x=s->data[s->top--];
    return 0;
}

 
 
1
2
3
4
5
6
7
8
9

1.2.5读栈顶元素

首先判断栈是否为空，如果为空，则返回-1；如果不为空，则返回栈顶元素，并返回0。

int GetTop(SqStack* s, ElemType *x)
{
    if(s->top==-1){
        return -1;
    }
    *x=s->data[s->top];
    return 0;
}
 
 
1
2
3
4
5
6
7
8

二.共享栈

2.1定义

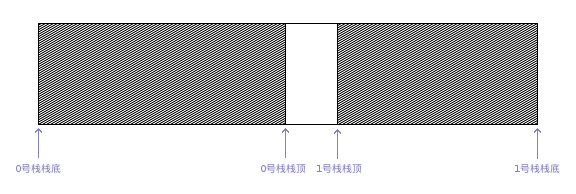
利用栈底位置相对不变的特性，可以让两个顺序栈共享一个一维数据空间，将两个栈的栈底分别设置在共享空间的两端，两个栈顶向共享空间中间延伸。如图所示：

则共享栈的数据结构可以描述为：

typedef struct{
    ElemType data[MaxSize];
    int top[2];
}SqStack;
 
 
1
2
3
4

这里对共享栈的判断条件进行说明。

• 栈空条件：0号栈【top[0]==-1】；1号栈【top[1]==MaxSize】
• 栈满条件：top1-top0=1

2.2基本操作

2.2.1初始化操作

完成对栈顶指针的复位操作，按照上述规定，0#栈为空，则top[0]==-1；若1#栈为空，则top[1]==MaxSize;

void InitStack(SqStack *s)
{
    s->top[0]=-1;
    s->top[1]=MaxSize;
}
 
 
1
2
3
4
5

2.2.2判空操作

同样根据上述规定，0#栈为空，则top[0]==-1；若1#栈为空，则top[1]==MaxSize；那么若两个栈均为空则返回0；如果栈不为空，则返回-1。

int StackEmpty(SqStack* s)
{
    if(s[0]->top==-1&&s[1]->top==MaxSize){
        return 0;
    }else{
        return -1;
    }
}
 
 
1
2
3
4
5
6
7
8

1.2.3入栈操作

先确定栈号是否合法，然后查看是对0#栈还是1#栈进行操作，入栈操作和顺序栈的入栈操作并无太大不同。选定之后进行入栈操作。这里应该注意此共享栈是否已满，如果已满则不能进行入栈操作。如若入栈成功则返回0；入栈失败则返回-1。

int Push(SqStack*s, ElemType x, int n)
{
    if(n<0||n>1){
        printf("The stack number is false!\n");
        return -1;
    }
    if(s->top[1]-s->top[0]==1){
        printf("The stack is full!\n");
        return -1;
    }
    switch(n){
        case 0:s->data[++s->top[0]]=x;break;
        case 1:s->data[--s->top[1]]=x;break;
    }
    return 0;
}
 
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

2.2.4出栈操作

先确定栈号是否合法，然后查看是对0#栈还是1#栈进行操作，出栈操作和顺序栈的出栈操作并无太大不同。选定之后进行出栈操作。如果出栈成功返回0；出栈失败返回-1。

int Pop(SqStack *s, ElemType* x,int n)
{
    if(n<0||n>1){
        printf("The stack number is false!\n");
        return -1;
    }
    switch(n){
        case 0:
            if(s->top[0]==-1){
                printf("The stack[0] is empty!\n");
            }
            *x=s->data[s->top[0]--];
            break;
        case 1:
            if(s->top[1]==MaxSize){
                printf("The stack[1] is empty!\n");
            }
            *x=s->data[s->top[1]++];
            break;
    }
    return 0;
}
 
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

三.链栈

3.1定义

采用链式存储的栈称为链栈。 
链栈的优点便是便于多个栈共享存储空间和提高其效率，而且不存在栈满上溢的情况。通常采用单链表实现，并规定所有的操作都是在单链表的表头进行的，这里规定链栈没有头节点。如图所示：

链栈的数据结构的描述如下：

typedef struct LinkNode{
    ElemType data;
    struct LinkNode *next;
}LinkStack;

 
 
1
2
3
4
5

因为采用链式存储时的栈与第1章的单链表操作类似，这里便不再详细说明。但应当注意区分带头结点的单链表与不带头结点的单链表操作略有不同。 

注：在栈的操作中，经常会求到对于n个不同的元素进栈，则出栈序列的个数为多少？ 
对于这种题，我们可以引入卡特兰（Catalan）数进行解决。答案为： 1n+1(2nn)