projecteuler No.78 Coin partitions

原文题目链接：

http://projecteuler.net/problem=78

翻译题目链接：

http://pe.spiritzhang.com/index.php/2011-05-11-09-44-54/79-78

通过人数：8032

题目分析：

粗一看，像是一道很经典的动态规划问题。于是我设基本状态(m,n)为m个硬币分n堆放所可以放的种类数，以(m,n)=(m-1,n-1)+(m-n,n)为递推关系，写出了如下代码：

#include<stdio.h>

int m[21000]={0};
int p[21000][21000]={0};

int main()
{
	for (int i = 1; i < 10000; i++)
	{
		for (int j = 1; j <= i; j++)
		{
			if (i == j)
				p[i][j] = 1;
			else
			{
				p[i][j] = p[i - 1][j - 1];
				if (i >= 2 * j)
					p[i][j] += p[i-j][j];
			}
			p[i][j] = p[i][j] % 1000000;
		}
		for (int j=1;j<=i;j++)
		{
			m[i] += p[i][j];
			m[i] = m[i] % 1000000;
		}
		if (m[i] == 0)
			printf("%d %d\n",i,m[i]);
	}
	return 0;
}

于是非常悲惨的发现：在内存允许范围内，没有找到...

接下来我尝试了将超过内存范围的地方使用递归，未超出的地方从数组取值的解法，但非常悲惨也非常正常的发现递归部分非常慢...一天之内算不完...

于是我上网查了一下资料，注意到了以下一片博文：

Project Euler 78: Investigating the number of ways in which coins can be separated into piles.

在这其中提到了维基百科中的这个条目：Partition(number theory)

那里有如下公式：（其中p(n)表示n个硬币的分堆数即整数n的分拆数）

.............................................（1）
上式将等号右边按等比级数分解之后其组合意义就显然了。上式的右边即为p(n)的母函数

而p(n)的母函数的倒数即为欧拉函数，其系数有五边形数定理：

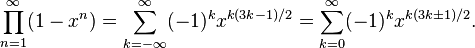
即：（等号右边的系数为广义五边形数）

（2）

将以上两式联立，有：

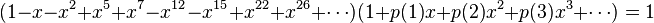
进行系数比较，即可得到p(n)的递推公式：

其减去的值的序列为广义五边形数序列，满足：

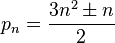
这下，有了比较好的公式，就可以做了~

解题过程（代码仅供参考，因为偷懒，代码风格什么的实在不好意思...）：

一、生成所需的广义五边形数序列：

int a[1000];
for (int i=0;i<1000;i++)
{
	int n=(i+1)/2;
	if (i%2==0)
		a[i]=(3*n*n+n)/2;
	else
		a[i]=(3*n*n-n)/2;
}

二、计算整数分拆序列并求出所需值：

int n[100000]={0};
n[0]=1;
for (int i=1;i<100000;i++)
{
	for (int j=1;a[j]<=i;j++)
	{
		if (j%4==1||j%4==2)
			n[i]+=n[i-a[j]];
		else
			n[i]-=n[i-a[j]];
	}
	n[i] = n[i] % 1000000;
	if (n[i]==0)
		printf("%d\n",i);
}

打印出所求值：55374

感觉还是要好好学习数学...这道题主要花的时间都花在错误的尝试和看数学证明上了。

以上只是我做题时的解法。

如果有更好的解法、更好的思路，欢迎评论讨论~O(∩_∩)O~