UVA | Coin Change

引入

Coin Changing Minimum Coins Dynamic Programming
给出N中不同金额的硬币，每种金币有无限多个。给定一个金额M，问最少需要多少个硬币可以凑成M？

熟悉的朋友一看这道题就知道是完全DP，具体也没有什么好说的了，不过这里还是推一推。

由Subset Sum Problem的推导我们知道，01背包其i状态完全依赖于i-1状态，在不需要还原具体解是如何的情况下，由二维可以压缩到一维。

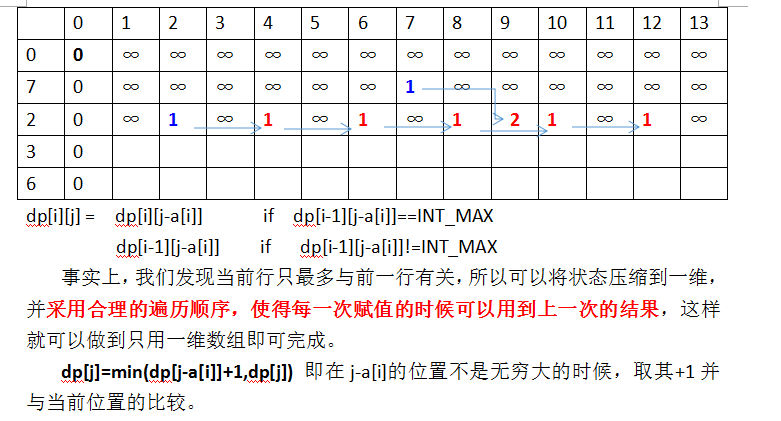
故可以得出DP方程并求解，其实和完全背包非常类似，只是所求值从最大值改为了最小。
带来的问题有初始化为最大值，以及判断是否为最大值才能相加的问题，这些都比较容易解决。

原题

Suppose there are 5 types of coins: 50-cent, 25-cent, 10-cent, 5-cent, and 1-cent. We want to make changes with these coins for a given amount of money.
For example, if we have 11 cents, then we can make changes with one 10-cent coin and one 1-cent
coin, two 5-cent coins and one 1-cent coin, one 5-cent coin and six 1-cent coins, or eleven 1-cent coins.
So there are four ways of making changes for 11 cents with the above coins. Note that we count that
there is one way of making change for zero cent.
Write a program to find the total number of different ways of making changes for any amount of
money in cents. Your program should be able to handle up to 7489 cents.
Input
The input file contains any number of lines, each one consisting of a number for the amount of money
in cents.
Output
For each input line, output a line containing the number of different ways of making changes with the
above 5 types of coins.
Sample Input
11
26
Sample Output
4
13

与上一题非常之类似，但是要求我们求的是总量。
我们不妨再列一个矩阵推一推：

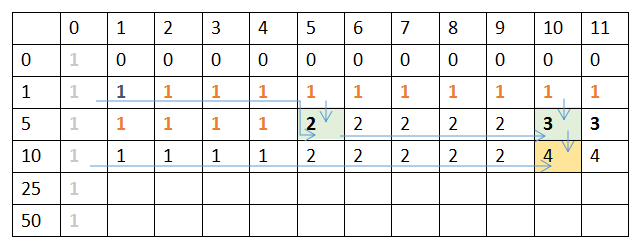
背包大小为0的时候肯定会有1种方式就是什么都不放.
只用硬币1时，我们知道所有的都仅有一种方式，从这里我们很难看出规律。

只用硬币1、5时，在背包大小为5的时候，我们知道应该有2种结果，考虑一下这个2从何而来：5个1组成 + 1个5组成
考虑：dp[2][5]=dp[1][5]+dp[1][5-5]=2，如图

在背包大小为10的时候，我们知道有3中情况，10个1、5*1+1*5、2个5。
组成5的情况有2种，这样如果+5的话，组成10也有2种，所以我们可以得到
如图所示，dp[2][10]=dp[1][10]+dp[2][10-5];
可能规律还不是很明显，我们继续推；

可以发现当a[i] > j【j为背包大小】的时候，dp[i][j]=dp[i-1][j] ，这个规律很显然。
当j=10时，我们知道多出来一个解就是，一个10.
我们知道dp[2][10]=3;而多出来的一种是dp[3][10-10]也就是3个硬币时，组成0有1种，于是加上10的话也仅仅有一种。

于是我们发现非常类似于完全背包，当前问题会重复利用到之前的子问题。可以写出dp方程
dp[i][j]=d[i-1][j]+d[i][j-a[i]]
实现的代码如下:

int dp[N][N]; 
class Solution{
public:
    int generate(vector<int> &coins,int target){
        memset(dp,0,sizeof(dp));
        //初始化背包为0的情况 
        for(int i=0;i<coins.size();i++)
        dp[i][0]=1;

        for(int i=0;i<coins.size();i++){
            for(int j=1;j<=target;j++){
                int val=i>0?dp[i-1][j]:0;
                if(j>=coins[i])
                dp[i][j]=val+dp[i][j-coins[i]];
                //注意处理j<coins[i]的情况
                else dp[i][j]=val;
            }
        }
        for(int i=0;i<coins.size();i++){
            for(int j=0;j<=target;j++){
                printf("%d ",dp[i][j]);
            }
            printf("\n");
        }

        return dp[coins.size()-1][target];
    }
};

同背包问题一样，我们发现其实第i步只用到了第i和i-1的状态，可以压缩到一维。
并且由于dp[j]一直处于相加的状态并会记录上一步的值，所以dp[i][j]=dp[i-1][j]这一步就默认做完了。
代码如下

int dp[N]; 
class Solution{
public:
    int generate(vector<int> &coins,int target){
        memset(dp,0,sizeof(dp));
        //初始化背包为0的情况 
        dp[0]=1;

        for(int i=0;i<coins.size();i++){
            for(int j=1;j<=target;j++){
                if(j>=coins[i])
                dp[j]+=dp[j-coins[i]];
            }
        }
        for(int i=0;i<=target;i++)
        printf("%d ",dp[i]);
        return dp[target];
    }
};

小结

背包DP问题相对来说题目的特征非常明显【对于较为简单的DP来说】所以这类问题可以往背包DP上靠。
但是状态方程的样式并不是一眼就能看出来，如果看不出来，一般来说可以拿一个二维矩阵推一推状态和阶段之间的关系，并找出其中的规律。
这是解答DP问题最本质的思想。