奇偶校验码

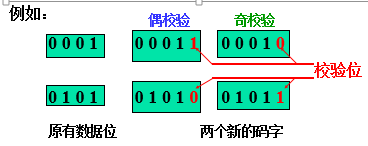
原理：在 k 位数据码之外增加 1 位校验位，
使 k+1 位码字中取值为 1 的位数保持为
偶数（偶校验）或 奇数（奇校验）

设x＝(加, x0 x1…xn-1 )是一个n位字, 则奇校验位Ｃ定义为
C ＝ x0⊕x1⊕…⊕xn-1
式中⊕代表按位只有当x中包含有奇数个1时,C＝0。

同理,偶校验位Ｃ定义为
C ＝ x0⊕x1⊕…⊕xn-1
即x中包含偶数个1时,才使C＝0。

 发送： x0 x1…xn-1C     （算出C加到需发送字的后面）
 接收： x0 ' x1 ' …xn-1 ' C ' 
 计算：F＝x'0⊕x'1⊕…⊕x'n-1⊕C '
 结果：若F＝1，意味着收到的信息有错；
             若F＝0，表明x字传送正确。

特点：
奇偶校验可提供单（奇数）个错误检测，
但无法检测多（偶数）个错误,
更无法识别错误信息的位置及纠正错误。