金字塔融合
原理:
将参加融合的的每幅图像分解为多尺度的金字塔图像序列,将低分辨率的图像在上层,高分辨率的图像在下层,上层图像的大小为前一层图像大小的1/4。层数为0,1,2……N。将所有图像的金字塔在相应层上以一定的规则融合,就可得到合成金字塔,再将该合成金字塔按照金字塔生成的逆过程进行重构,得到融合金字塔。
这个总的思路就是一下所有基于金字塔融合的算法过程,不同点就在于分解构造的金字塔不同,每层的融合规则不一样,重构的方法不同而已。金字塔方法最先实现了这种思想,之后小波方法进一步完善和发展了这种多尺度融和的思想。
高斯金字塔
高斯金字塔是最基本的图像塔。首先将原图像作为最底层图像G0(高斯金字塔的第0层),利用高斯核(5*5)对其进行卷积,然后对卷积后的图像进行下采样(去除偶数行和列)得到上一层图像G1,将此图像作为输入,重复卷积和下采样操作得到更上一层图像,反复迭代多次,形成一个金字塔形的图像数据结构,即高斯金字塔。
高斯金字塔的构建过程为:假设高斯金字塔的第L层图像为Gl:
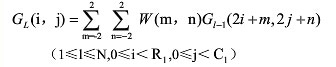
式中N为高斯金字塔顶层层号,Rl和Cl分别为高斯金字塔第l层的行数和列数。W(m,n)是一个二维可分离的5*5窗口函数,表达式为:








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








