【POJ1171】【线段树+扫描线】【矩形周长】【坑区间要分3类讨论】

Language: Default Picture Time Limit: 2000MS   Memory Limit: 10000K Total Submissions: 11200   Accepted: 5915 Description A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter.  Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1. 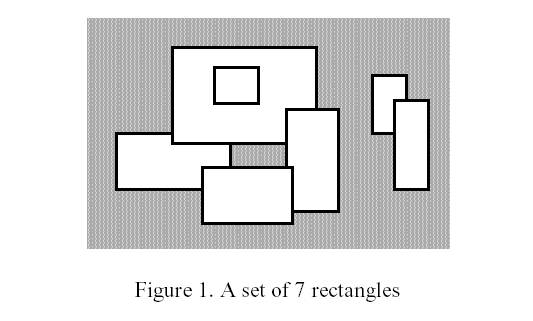 The corresponding boundary is the whole set of line segments drawn in Figure 2. 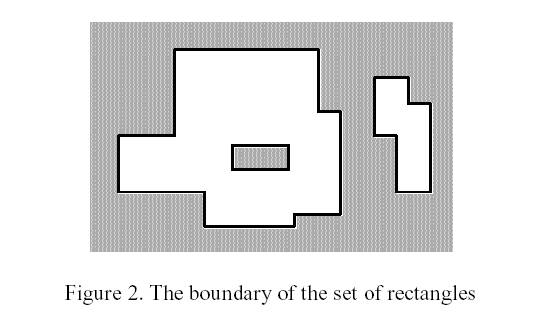 The vertices of all rectangles have integer coordinates.  Input Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate.  0 <= number of rectangles < 5000  All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area. Output Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles. Sample Input 7 -15 0 5 10 -5 8 20 25 15 -4 24 14 0 -6 16 4 2 15 10 22 30 10 36 20 34 0 40 16 Sample Output 228 Source IOI 1998

[Submit]   [Go Back]   [Status]   [Discuss]

首先，周长是什么？

周长是线段的长度。 是哪些线段呢？  投影下来的线段。  那么投影下来的线段在原矩形的什么位置呢。  投影下来的线段 一定是在原矩形的4边上。

用2根 平行于x轴的直线进行扫描, 然后再沿着y轴方向进行投影。 如果一根线段（X1,X2,Y）被覆盖了，那么一定存在一边yi < Y， 存在另外一边yj > Y。所以自下往上，第一次投影下来（沿着y轴投影）的位置一定是周长， 然后第二次的如果落在了 第一次投影的线段中，那么我们知道 重叠的不能计算。  那么第二次的全部投影长度-第一次的全部投影长度就是新增的横向的投影周长。 纵向的 一根的长度很好知道， 那么有多少根呢？ 其实就是染色区间的数量。  坑点就是 区间要分三类讨论。。。 

#include <iostream>
#include <cstring>
#include <cmath>
#include <queue>
#include <stack>
#include <list>
#include <map>
#include <string>
#include <cstdlib>
#include <cstdio>
#include <algorithm>
using namespace std;

#define rep(i,a,n) for (int i=a;i<n;i++)
#define per(i,a,n) for (int i=n-1;i>=a;i--)
#define mp push_back
#define lson l,m,rt<<1
#define rson m,r,rt<<1|1

struct Line
{
	int l,r,y,s;
	Line() {};
	Line(int ll,int rr,int yy,int ss):l(ll),r(rr),y(yy),s(ss){};
}line[10010];
int X[10010];
int color[10010*4];
int numseg[10010*4];
int len[10010*4];
bool lbd[10010*4],rbd[10010*4];

int cmp(Line a,Line b)
{
	return a.y < b.y;
}

int n;
int t;

void build(int l,int r,int rt)
{
	lbd[rt] = rbd[rt] = 0;
	len[rt] = 0;
	numseg[rt] = 0;
	color[rt] = 0;
	if(r - l == 1) return ;

	int m = (l + r) >> 1;
	build(lson);
	build(rson);
}

void PushUp(int rt,int l,int r)
{
	if(color[rt] > 0)
	{
		lbd[rt] = rbd[rt] = true;
		len[rt] = X[r] - X[l];
		numseg[rt] = 1;
		return ;
	}
	if(r - l == 1)
	{
		lbd[rt] = rbd[rt] = false;
		len[rt] = 0;
		numseg[rt] = 0;
	}
	else
	{
		lbd[rt] = lbd[rt<<1];
		rbd[rt] = rbd[rt<<1|1];
		numseg[rt] = numseg[rt<<1] + numseg[rt<<1|1];
		if(rbd[rt<<1] && lbd[rt<<1|1])
		{
			numseg[rt] -= 1;
		}
		len[rt] = len[rt<<1] + len[rt<<1|1];
	}
}

void update(int L,int R,int add,int l,int r,int rt)
{
	if(L == X[l] && R == X[r])
	{
		color[rt] += add;
		PushUp(rt,l,r);
		return ;
	}

	int m = (l + r) >> 1;
	if(L <= X[m-1]) update(L,min(R,X[m]),add,lson);
	if(X[m] <= R-1) update(max(L,X[m]),R,add,rson);
	PushUp(rt,l,r);
}
int main()
{
	freopen("in.txt","r",stdin);
	while(scanf("%d",&n) != EOF)
	{
		t = 0;
		for(int i=0;i<n;i++)
		{
			int x1,y1,x2,y2;
			scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
			line[t] = Line(x1,x2,y1,1);
			X[t ++] = x1;
			line[t] = Line(x1,x2,y2,-1);
			X[t ++] = x2;
		}
		sort(line,line+t,cmp);
		sort(X,X+t);
		int MAXN = unique(X,X+t) - X;
		build(0,MAXN-1,1); 
		int ans = 0;
		int pre = 0;
		for(int i=0;i<t-1;i++)
		{
			update(line[i].l,line[i].r,line[i].s,0,MAXN-1,1);
			ans += abs(len[1] - pre);
			pre = len[1];
			ans += numseg[1] * 2 * (line[i+1].y - line[i].y);
		}
		update(line[t-1].l,line[t-1].r,line[t-1].s,0,MAXN-1,1);
		ans += abs(len[1] - pre);
		printf("%d\n",ans);
	}
}