leetcode --- 2 sum , 3 sum , 4 sum , k sum problem

最新推荐文章于 2018-08-17 17:29:01 发布

NeverMore_7

最新推荐文章于 2018-08-17 17:29:01 发布

阅读量1.2k

点赞数

本文链接：https://blog.csdn.net/unixtch/article/details/52724125

版权

算法和数据结构同时被 2 个专栏收录

10 篇文章 0 订阅

订阅专栏

C/C++

6 篇文章 0 订阅

订阅专栏

K Sum Problem

Leetcode上有2 sum problem，3 sum problem， 4 sum problem，K sum problem等问题，为方便讨论，从最简单的2 sum入手，讨论到更一般的K sum problem，这类问题一般具有这样的形式：

给定一个n长度的数组array和一个target，在数组中寻找k个数，使这k个数的和等于target，并且不存在相同的结果集。

·题目链接

2. sum：https://leetcode.com/problems/two-sum/

3. sum：https://leetcode.com/problems/3sum/

4. sum：https://leetcode.com/problems/4sum/

·2 sum problem

在数组中寻找两个数，使之和为target。

·2.1 暴力求解，这是最最朴素的解法，也是最容易想到的，但时间复杂度过高，在本题中，时间复杂度为O(n^2)。

·2.2 排序搜索，先将数组排序，设置首尾指针start,end，当start<end时，t_result=array[start]+array[end]如果 t_result == target,返回;如果t_result > target,--end; 如果t_result < target，++start; 否则没有两个数的和为target。该算法排序的时间复杂度为O(nlgn)，搜索的时间复杂度为O(n)，总的时间复杂度为O(nlogn)。

·2.3 Hash判断,把数组array中的每一个元素，存储在hash表中，接着检查每个元素的target-array[i]的值是否存在于hash表中，如果存在则存在两个数的和为target，如果检查完毕，那么没有。该算法的时间复杂度只是在扫描数组的所有元素有消耗，所以，总的时间复杂度为O(n)。

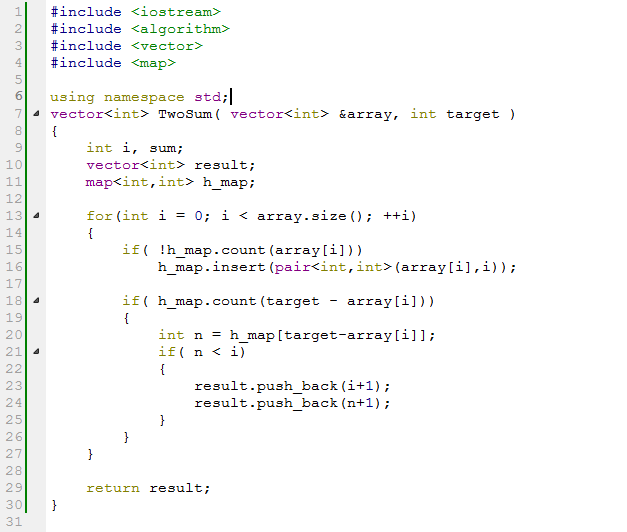
·3 sum problem

3 sum 和 2 sum 一样，只是寻找的是3个数的和，这个问题当然也可以暴力求解，依旧是时间复杂度的问题，暴力求解的时间复杂度是O(n^3)，第二种方法是先取数组中一个数，问题就转化为2 sum的问题求解，当数组中所有的数都被选定过后，问题也就解决了。例如“abcdf”，先取a，那么问题就是在bcdf中寻找两个数的和为target-a，然后取b,这个时候问题转化为cdf中寻找和为target-b的2 sum问题，a就不必再算入找寻找集合中，为什么？简单的证明即可：

第一次取a，问题转化为bcdf重寻找和为target-a的2 sum问题，假设其中一个数是b,那么有：

1.如果找不一个数加上a+b等于target，当选定b为第一个数时，如果第二个数选到了a，依旧不会有数满足该条件；

2.如果能找到一个数加上a+b等于target，那么这个数时唯一确定的，当选定b为第一个数时，如果第二个数又选到a,那么这个数也唯一确定，且和选定a为第一个数，b为第二个数的最后一个数相等，那么结果集重复。再回想选取第一个数和第二个数的方式，就可以知道，在选定一个数为第一个数后，这个数后面的数都会依次被选取，如果在后面的选取中，有选择了前面的数，那么结果集肯定会重复，这样就增加了不必要的选取和计算，影响效率。至于如何筛选重复的结果集，请继续往下面看。

针对3 sum问题转化成2 sum问题求解，那么是利用什么方法解决2 sum问题，然后再求取3 sum问题会好点了？摒弃暴力求解的方式，利用hash还是排序搜索？单从方法上讲，前者肯定由于后者，但有一个问题，如果用hash，选取第一个数时，需要便利一次数组，再存入hash，再检查hash，而C++提供的map不支持改变KEY，相对比较麻烦，排序搜索的方式，只需要排序、移动首尾指针，再检查。其中利弊自己体会。

·4 sum problem

和3 sum问题一样，4 sum可根据相同的方式转换成2 sum问题，只不过要先选定2个数。

当然3 sum和4 sum依然可以用hash的方式来解决，例如对3 sum，可先将任何不同位置的两个值的和求得存入hash中，再用选取的第一个数去检查hash。但是这种方式不太好检查是哪两个数的和，如果是进行是否存在检查还是很方便的。

·针对算法的优化和去重复

可以选取所有的结果集后，再去重，这时候去重可以用hash去重，检查每组解是否一样。当然更好的方法就在求取解得过程中去重，这样能减少计算，结果中去重，可先将原数组排序，假设排序后为a a b c d，那么选取第一个a后，第二个a可以跳过不选，但是如果是 -1,-1,-1,2这样，选取第一个-1后，会有两组解-1,-1,2,这样还是会存在重复解，也就是说在求取过程中不能完全去除重复解，求取解后，还得再一次去除重复解，而经过排序后，就算有重复解，那么重复解的元素相对次序也是一样的，这个时候去重复的话也会很简单。具体看代码：

vector threeSum( vector &num )
{
    vector vecResult;
    if( num.size() < 3 )
        retrun vecResult;
    vector tripVec(3,0);
    sort(num.begin(),num.end());
    int currentVal = num[0];
    int iCount = num.size()-2;      // 最后一组情况
    for( int i = 0; i < iCount; ++i)
    {
        if( i && num[i] == currentVal ) //出去a a b c d中的a这种状况
            continue;
        tripVec[0] = num[i];
        int j = i + 1;
        int k = num.size() - 1; 
        while( j < k )
        {
            int tsum = num[j] + num[k];
            if( tsum + tripVec[0] == 0 )
            {
                tripVec[1] = num[j];
                tripVec[2] = num[k];
                vecResult.push_back(tripVec);
                ++j;
                --k;
            }
            else if(tsum + tripVec[0] < 0)
            {
                ++j;
            }
            else
                --k;
        }
    }
    vector::iterator it = unique(vecResult.bengin(),vecResult.end());  // 最后一次去重复
    vecResult.resize(distance(vecResult.begin(),it));
    return vecResult;
}

更多的讨论请参见：http://www.sigmainfy.com/blog/summary-of-ksum-problems.html,该文章对K sum有更详细的讨论。