平面点集的凸包

概念：给定一个平面的点集q，求覆盖所有点的最小凸多边形（在多边形边上，或内部）。
主要求解思想：
采用分治算法

如图，先找出y坐标最大和做小的点，并入此多边形的顶点集（因为是y坐标最大和最小，所以此直线左边和右边的凸包合起来还是凸包)；
对直线左右的点进行递归处理：
如直线左边，先找到一个离直线最远的点p并入多边形顶点集，连接p和ymin和ymax(因为是离直线d最远的点， 所以直线a左边的凸包和b上边的凸包合起来还是凸包，如图：

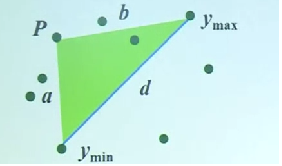
然后分别对直线a左边和直线b上边的点递归处理。
最后得到多边形的顶点集。
算法时间复杂度：0（$n^{2}$)

注：图片截取于https://class.coursera.org/algorithms-001/lecture/81