本篇博客主要是参考吴恩达教授的Ufldl教程,教程链接如下:
http://ufldl.stanford.edu/wiki/index.php/Softmax%E5%9B%9E%E5%BD%92
OK!开启,本次的学习之旅吧!
1、Softmax回归解决什么问题呢?
通过前面的学习,我们知道线性回归解决的连续值的预测,逻辑回归解决的是离散值的预测,而且针对二分类问题。那么问题来了,如果是离散值预测,但是是多类别预测,也就是有多个类别标签,这种情况怎么办呢?Softmax回归针对的就是这种问题。
2、Softmax回归的假设函数
还记得逻辑回归中的假设函数吗?不记得也没关系,逻辑归回的假设函数如下:
逻辑回归的假设函数借用了sigmoid函数,而且逻辑回归中有一个假设上式代表取类别1的概率,而取类别0的概率我们用1-h(x)表示。
在 softmax回归中,我们解决的是多分类问题(相对于 logistic 回归解决的二分类问题),类标  可以取
可以取  个不同的值(而不是 2 个)。因此,对于训练集
个不同的值(而不是 2 个)。因此,对于训练集  ,我们有
,我们有 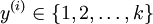 。(注意此处的类别下标从 1 开始,而不是 0)。对于给定的测试输入
。(注意此处的类别下标从 1 开始,而不是 0)。对于给定的测试输入  ,我们想用假设函数针对每一个类别j估算出概率值
,我们想用假设函数针对每一个类别j估算出概率值 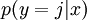 。也就是说,我们想估计
。也就是说,我们想估计  的每一种分类结果出现的概率。因此,我们的假设函数将要输出一个
的每一种分类结果出现的概率。因此,我们的假设函数将要输出一个  维的向量(向量元素的和为1)来表示这
维的向量(向量元素的和为1)来表示这  个估计的概率值。 具体地说,我们的假设函数
个估计的概率值。 具体地说,我们的假设函数 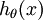 形式如下:
形式如下:
其中 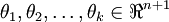 是模型的参数。请注意
是模型的参数。请注意 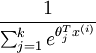 这一项对概率分布进行归一化,使得所有概率之和为 1
这一项对概率分布进行归一化,使得所有概率之和为 1
3、代价函数
先给出Softmax的函数形式如下:
这个公式是怎么来的呢?我们可以从逻辑回归的代价函数推广而来。
 分类为类别 j
的概率为:
分类为类别 j
的概率为:
在逻辑回归中我们梯度下降法求解最优值,Softmax回归也是用梯度下降法求解最优值,梯度公式如下:
4、Softmax回归模型参数具有“冗余”性
冗余性指的是最优解不止一个,有多个。假设我们从参数向量  中减去了向量
中减去了向量  ,这时,每一个
,这时,每一个  都变成了
都变成了 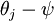 (
(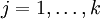 )。此时假设函数变成了以下的式子:
)。此时假设函数变成了以下的式子:
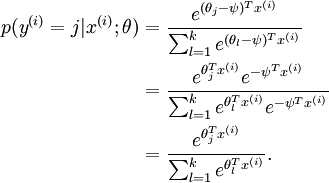
 中减去
中减去
 完全不影响假设函数的预测结果!这就是Softmax回归的冗余性。
完全不影响假设函数的预测结果!这就是Softmax回归的冗余性。
5、权重衰减
针对上述的冗余性,我们应该怎么办呢?权重衰减可以解决这个问题。
我们通过添加一个权重衰减项 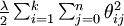 来修改代价函数,这个衰减项会惩罚过大的参数值,现在我们的代价函数变为:
来修改代价函数,这个衰减项会惩罚过大的参数值,现在我们的代价函数变为:
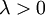 ),代价函数就变成了严格的凸函数,这样就可以保证得到唯一的解了。
),代价函数就变成了严格的凸函数,这样就可以保证得到唯一的解了。
为了使用优化算法,我们需要求得这个新函数  的导数,如下:
的导数,如下:
通过最小化  ,我们就能实现一个可用的 softmax 回归模型。
,我们就能实现一个可用的 softmax 回归模型。
当类别数 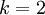 时,softmax 回归退化为 logistic 回归。这表明 softmax 回归是 logistic 回归的一般形式。具体地说,当
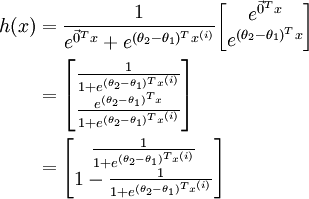
时,softmax 回归退化为 logistic 回归。这表明 softmax 回归是 logistic 回归的一般形式。具体地说,当 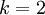 时,softmax 回归的假设函数为:
时,softmax 回归的假设函数为:
利用softmax回归参数冗余的特点,我们令 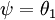 ,并且从两个参数向量中都减去向量
,并且从两个参数向量中都减去向量  ,得到:
,得到:
因此,用 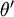 来表示
来表示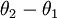 ,我们就会发现 softmax 回归器预测其中一个类别的概率为
,我们就会发现 softmax 回归器预测其中一个类别的概率为 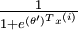 ,另一个类别概率的为
,另一个类别概率的为 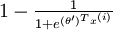 ,这与 logistic回归是一致的。
,这与 logistic回归是一致的。








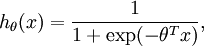
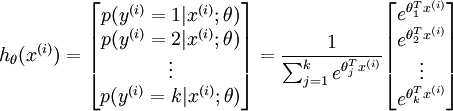
![\begin{align}J(\theta) = - \frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=1}^{k} 1\left\{y^{(i)} = j\right\} \log \frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{ \theta_l^T x^{(i)} }}\right]\end{align}](http://ufldl.stanford.edu/wiki/images/math/7/6/3/7634eb3b08dc003aa4591a95824d4fbd.png)
![\begin{align}J(\theta) &= -\frac{1}{m} \left[ \sum_{i=1}^m (1-y^{(i)}) \log (1-h_\theta(x^{(i)})) + y^{(i)} \log h_\theta(x^{(i)}) \right] \\&= - \frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=0}^{1} 1\left\{y^{(i)} = j\right\} \log p(y^{(i)} = j | x^{(i)} ; \theta) \right]\end{align}](http://ufldl.stanford.edu/wiki/images/math/5/4/9/5491271f19161f8ea6a6b2a82c83fc3a.png)



![\begin{align}J(\theta) = - \frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=1}^{k} 1\left\{y^{(i)} = j\right\} \log \frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{ \theta_l^T x^{(i)} }} \right] + \frac{\lambda}{2} \sum_{i=1}^k \sum_{j=0}^n \theta_{ij}^2\end{align}](http://ufldl.stanford.edu/wiki/images/math/4/7/1/471592d82c7f51526bb3876c6b0f868d.png)
![\begin{align}\nabla_{\theta_j} J(\theta) = - \frac{1}{m} \sum_{i=1}^{m}{ \left[ x^{(i)} ( 1\{ y^{(i)} = j\} - p(y^{(i)} = j | x^{(i)}; \theta) ) \right] } + \lambda \theta_j\end{align}](http://ufldl.stanford.edu/wiki/images/math/3/a/f/3afb4b9181a3063ddc639099bc919197.png)
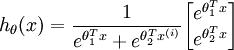














 1146
1146











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








