堆与堆排序之初见

堆（本文只提二叉堆，当然也有多叉堆）作为一种数据结构，是一个数组，可以被看成是一个近似的完全二叉树，树上的每一个节点对应数组中的一个元素，并且除了最底层节点外，该树是完全充满的，而且是从左向右依次填充。
我们目前经常听到的名词“堆”已经被引申为“垃圾收集存储机制”，但本文提及的“堆”指的是堆数据结构。
为了后续描述方便，我们定义堆的数组为H，用H.length表示堆数组的大小，用H.size表示堆中存储的有效元素的个数，此外，也假设堆数组中元素是从下标为1的位置开始存储，也就是说，树的根节点是H[1]。在堆中，给定一个节点i，可以很容易的计算出它的父节点和孩子节点。伪代码为：

PARENT(i): //求父节点
return i/2;

LEFT(i) : //求左孩子节点
return 2*i;

RIGHT(i) ://求右孩子节点
return 2*i+1;

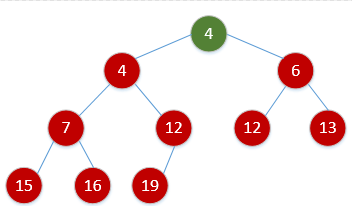
可以看一个例子：

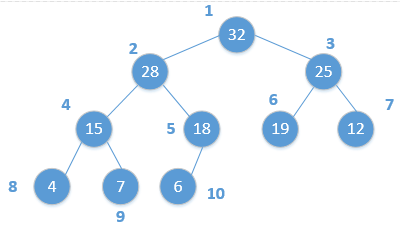
由上图可以看出，对于节点2来说，它的父节点编号为 2/2=1，孩子节点分别为2*2=4和2*2+1=5。

二叉堆分为最大堆和最小堆两种，最大堆中，除了根节点，其他的节点都需要满足：H[PARENT(i)]>=H(i);也就是说，其父节点的值大于等于自身节点值。最小堆中，除了根节点，其他的节点都需要满足：H[PARENT(i)]<=H(i);也就是说，其父节点的值小于等于自身节点值。

现在，我们考虑如何将一个无序的数组调整为最大堆（最小堆调整方式与最大堆类似）。我们注意到，在堆数组中，子数组H[H.size/2+1…H.size]中的元素都是树的叶子节点，每一个叶子节点已经满足最大堆的性质，因此，为了将堆调整为最大堆，我们只需要调整数组中的非叶子节点即可，也就是说，应该从树的第一个非叶子节点开始进行调整。如果定义堆调整的过程为：Heap_Adjust(H, i),那么，建立最大堆的过程描述为：

Build_Heap(H):
for : i = A.size / 2 to 1
	Heap_Adjust(H, i);

现在，考虑堆调整Heap_Adjust(H, i)过程。
我们假定该过程中，根节点为LEFT(i)和RIGHT(i)的二叉树都是最大堆，但此时，H(i)可能小于孩子节点，这样就违背了最大堆的性质。因此，Heap_Adjust过程就是通过让H(i)的值在最大堆中“逐级下降”，从而使得以下标i为根节点的子树重新满足最大堆的性质。

使用伪代码描述该过程为：

Heap_Adjust(H, i) :
l = LEFT(i)
r = RIGHT(i)
if l <= H.size and H[l] > H[i]
	largest = l
else largest = i
if r <= H.size and H[r] > H[largest]
	largest = r
if largest != i
	swap(H[i], H[largest])
	Heap_Adjust(H, largest)

我们通过实例来理解这个过程，假设某一时刻，对数组中的元素状态为：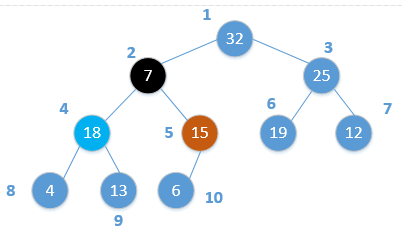

我们对节点2进行调整，可以看到，其孩子节点4和5均满足最大堆性质。由上述Heap_Adjust过程知，此时，i=2，l=4，r=5，而largest=4，因为largest！=i，因此，需要交换节点4和节点2的值，交换后为：

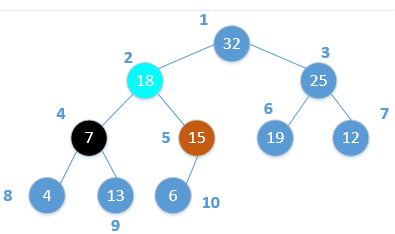
调整后，对于节点2和其孩子节点4和5来说，已经满足最大堆性质，但却打破了节点4及其孩子节点的最大堆性质。因此，需要对节点4递归进行调整。

有了上述堆的基本操作，我们再分析堆排序过程。
初始时候，对于一无序数组，首先利用Build_Heap(H)过程，建立一最大堆，因为对于最大堆来说，数组中的最大元素始终处于H[1]的位置，因此，通过将H[1]与H[H.size]交换，也就是将堆中第一个元素与最后一个元素交换位置，然后，在堆中去掉最后一个元素（H.size=H.size-1）。对于剩余的节点来说，因为根节点可能会违背最大堆的性质，所以需要通过Heap_Adjust(H, 1)过程对剩余元素重新构建一个最大堆。总体来看，堆排序就是不断重复这一元素交换与堆调整的过程。
伪代码描述为：

HeapSort(H):
Build_Heap(H)
for i = H.size to 2:
	swap(H[1], H[i])
	H.size = H.size - 1
	Heap_Adjust(H, 1)

通过简单的例子展现出这一过程，如下（图顺序为从左到右，从上到下，从堆调整开始）：

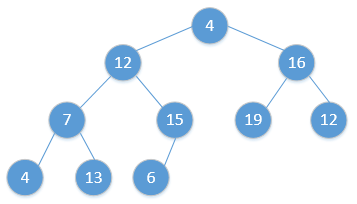
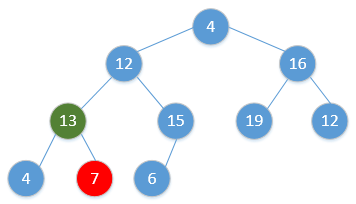
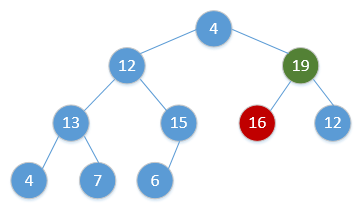
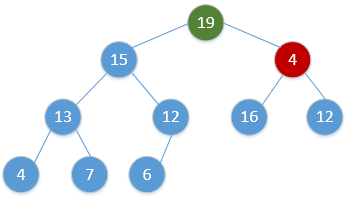
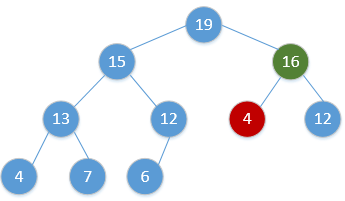
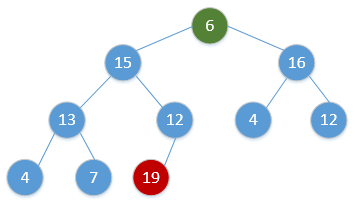
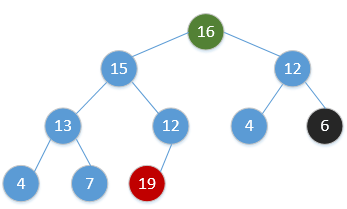
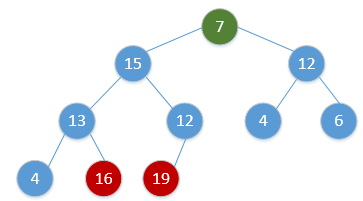
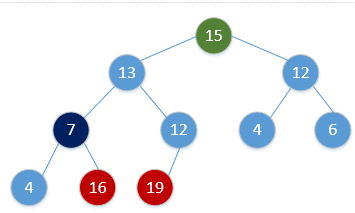
继续重复该过程，最终会得到：

堆排序的时间复杂度是O(nlgn)，因为每次调用Build_Heap的时间复杂度是O(n)，而n-1次调用Heap_Adjust，每次的时间复杂度是O(lgn)。

附上堆操作过程C语言实现代码：

/*
 * 建立一个最大堆
 */
void buildHeap(int array[], int size)
{
	//从最后一个非叶子节点开始调整堆元素
	for (int i = size / 2; i >= 1; i--)
	{
		heapAdjust(array, i, size - 1);
	}
}

/*
  堆调整递归函数方式
*/
void heapAdjust(int array[], int start, int end)
{
	int right = 2 * start + 1;
	int left = 2 * start;

	if (start > end)
	{
		return;
	}
	int largest;

	if (left <= end && array[left] > array[start])
	{
		largest = left;
	}
	else
	{
		largest = start;
	}
	if (right <= end && array[right] > array[largest])
	{
		largest = right;
	}
	if (largest != start)
	{
		int temp = array[start];
		array[start] = array[largest];
		array[largest] = temp;
		heapAdjust(array, largest, end);
	}

}

/*
  堆调整非递归实现方法
*/
void heapAdjust2(int array[], int start, int end)
{
	int temp = array[start];
	
	for (int i = 2 * start; i <= end; i*=2)
	{
		if (i < end && array[i] < array[i + 1])//左右孩子比较
		{
			i++;//右孩子较大
		}
		if (temp < array[i])//孩子比父节点大,则交换
		{
			array[start] = array[i];
			start = i;
		}
		else //满足大顶堆条件，退出调整
		{
			break;
		}

	}
	array[start] = temp;
}

/*
 堆排序，从小到大排序
*/
void heapSort(int array[], int size)
{
	//最后一个元素与第一个元素进行交换
	for (int i = size; i > 1; i--)
	{
		int temp = array[1];
		array[1] = array[i];
		array[i] = temp;

		//进行堆调整
		heapAdjust(array, 1, i - 1);
	}
}