关于快速排序（QuickSort）的一些总结

weijiaduo

已于 2022-09-10 18:05:33 修改

阅读量1.2k

点赞数 5

分类专栏： Java 算法文章标签：算法快速排序

于 2018-08-26 13:26:54 首次发布

本文链接：https://blog.csdn.net/u013447565/article/details/82079959

版权

Java 同时被 2 个专栏收录

2 篇文章

订阅专栏

算法

1 篇文章

订阅专栏

前言：最近又写到了有关快速排序的代码，结果半天写不对。从代码的整体上来说，代码结构是没问题的，就是在边界问题上出现了错误，经过一番思考以及查询资料，终于完美解决了，因此特地小记一下。

文章目录

一. 简介

快速排序算法，它的基本原理是：通过一趟排序将数据分割成两部分，其中一部分数据都比另外一部分数据都要小，然后再对这两部分数据分别进行快速排序，以此达到数据的排序。其基本逻辑代码如下：

    public void quickSort(int[] a, int left, int right) {
        if (left < right) {
            int mid = partSort(a, left, right);
            quickSort(a, left, mid - 1);
            quickSort(a, mid + 1, right);
        }
    }

二. 排序原理

快速排序最关键的部分就是如何将大小两部分数据分离，也就是上述代码中的 partSort 的实现。

下面我用一个例子来介绍一下 partSort 的基本原理，假设要对数组进行从小到大的排序：

(1) 首先给定需要排序的数组：
初始数组

(2) 选定一个基准值，这里暂时使用最左端的值（也就是5）：
选定基准值

(3) 接着利用两个指针分别从数组左端和右端去遍历数据，从左端出发的指针找到比基准值大（> 5）的值时则停止，从右端出发的指针找到比基准值小（< 5）的值时则停止：
开始遍历
此时两个指针都停在了对应的值的位置，左指针指向7，右指针指向1：
遍历完成

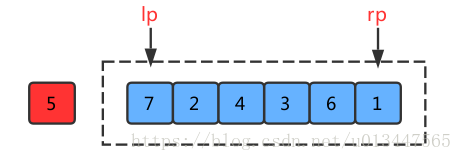
(4) 然后将这两个位置的数据进行交换，交换完成之后再执行第3步，直到两个指针相遇（也就是指向同一个位置）时结束交换：

(5) 最后一步就是将指针相遇点的值与基准点的值进行交换：
交换基准点

至此，按照基准值为标准，partSort 已经将大小两部分数据分离，完成了快速排序的一次排序过程，而基准值（就是5）也放在了最终排序结果中它应该放置的地方。

也就是说，快速排序的每一轮 partSort 排序结果，都会将基准值放在它最终排序序列的正确位置。

三. 基准点以及指针移动顺序

前面已经简单介绍了排序的过程，其中有几个比较关键的地方：

基准值的选取
基准点
指针的先后移动顺序

基准值的选取
其实基准值的选取没什么好说的，一般都是取最左端或者最右端的值，当然了，如果有时候对排序要求比较高的话，还可以随机取值或者三元取值（最左端，中点，最右端）等各种取值方法，我不过多介绍，因为这不是我的关注重点。

基准点
什么是基准点，也就是我们平时进行 partSort 排序前，一般都会将基准值放在数组的最左端或者最右端，这两个位置就是基准点。

指针的先后移动顺序
因为排序时需要两个指针分别在两端往中间移动，那这两个指针谁先移动谁后移动呢？还是说不论谁先移动都不会影响最终排序结果呢？

很明显，基准值只会影响排序的速度，而不会影响最终的排序结果，因此此处不讨论。

那基准点和指针先后顺序是否会影响排序的正确性呢？下面我就用例子验证一下这个问题。

根据基准点和指针先后顺序，可以分为四种情况：

基准点左端，指针移动先右后左
基准点左端，指针移动先左后右
基准点左端，指针移动先右后左
基准点右端，指针移动先左后右

在验证这几种情况之前，先给出需要排序的数组，假设要将数组按从小到大排序，并选取5为基准值：
初始数组

3.1 例子演示

(1) 基准点左端，指针移动先右后左
开始遍历
那么按照之前 partSort 的排序，最终两指针相遇的位置如下：

最后交换基准值与指针相遇点的值：
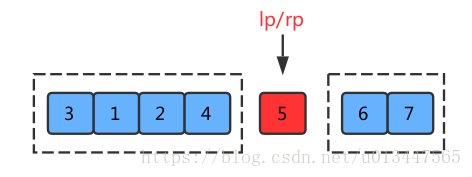
这里写图片描述
好的，这里得到的结果没问题，后续执行也没有问题，这里就不贴图了。

(2) 基准点左端，指针移动先左后右

开始遍历

那么按照之前 partSort 的排序，最终两指针相遇的位置如下：

最后交换基准值和相遇点的值（注意，这里两指针相遇的位置变化了，原来相遇的是3，现在是6）：

到这里就已经可以知道结果了，排序已经出错了。

再对另外两种情况（基准点在最右端时）进行分析的时候，也会发现，同样有一种情况结果正确，另一种情况却会失败。

这里我就不再贴图分析了，下面来分析一下为什么会出现这种问题。

3.2 分析总结

要分析出现问题的原因，首先必须要明确以下两点：

基准值在经过一轮排序之后，它所在的位置必定是它在最终排序序列的正确位置；
与基准值交换的值（也就是指针相遇的值）必须属于基准点所在的这一边。

根据这两条规则，可以知道情况2中出现问题的原因正是指针相遇的位置不正确（也就是指针相遇的值不属于基准点所在这一边），导致与基准值交换之后出现排序错误。那怎么保证最后指针能指向正确的位置呢？下面先给出结论：

基准点在最左端时，指针移动先右后左；
基准点在最右端时，指针移动先左后右。

为什么这样做就可以保证指针相遇的位置是正确的呢？假设要对一个数组进行从小到大的排序，并且选取基准点为最左端。由于左右指针相遇点的值要和基准值交换，那么只有左右指针相遇点的值是属于 左端（基准点所在这一边） 时，排序结果才会是正确的。

那如何保证指针相遇值是属于左端呢？如果是先移动右指针，再移动左指针，因为右指针先停止移动，左指针再停止移动，那么左右指针相遇时指向的值必然是满足右指针停止条件的值，而满足右指针停止的值必然不大于基准值，也就是说能够保证相遇点的值是属于左端的，可以和基准值交换。反之，如果是先移动左指针，再移动右指针，无法保证相遇值肯定属于左端。

同理，当基准点在右端时，先移动左指针，再移动右指针，也能够保证排序的正确性。

因此，只要记住一点，让基准点对面的的指针先走，这样就能够得到正确的排序结果。

四. 基准值的问题

这里讨论的基准值的问题指的是，当排序左右指针移动过程中，如果遇到与基准值相等的值，此时是应该跳过还是停止？

为了分析这个问题，首先给出一份 “partSort” 的代码：

	/**
     * 从小到大（一般方法）
     */
    public static int partSortLeft(int[] a, int left, int right){
        if (a == null || left > right) {
            return -1;
        }

        // 左端基准值
        int x = a[left];
        int lp = left, rp = right;
        while (lp < rp) {
            // 先右遍历取小值
            while (lp < rp && a[rp] >= x) {
                rp--;
            }

            // 再左遍历取大值
            while (lp < rp && a[lp] <= x) {
                lp++;
            }

            if (lp < rp) {
            	swap(a, lp, rp);
            }
        }

        // 交换基准值
        if (left < lp) {
        	swap(a, left, lp);
        }

        return lp;
    }

可以看到，上述代码是按从小到大排序，最左端为基准点，指针是先右后左。根据上面的讨论结果，这样的排序是没有问题的。

但是现在要讨论的不是这个，在上面的代码中，有两条关键语句：

 // 先右遍历取小值
 while (lp < rp && a[rp] >= x) {
	 rp--;
 }

 // 再左遍历取大值
 while (lp < rp && a[lp] <= x) {
	 lp++;
 }

需要注意的是 a[rp] >= x 和 a[lp] <= x 这两个地方，其中的 “>=” 和 “<=” 能不能换成其他的符号呢？例如换成 “>” 和 “<”？

一样地，根据不同的大小符号，可以分为四种情况：

a[rp] > x，a[lp] < x
a[rp] >= x，a[lp] < x
a[rp] >= x，a[lp] <= x
a[rp] > x，a[lp] <= x

下面用例子来对这几种情况进行说明。

4.1 例子演示

下面分别对这几种情况进行分析，代码依旧参考前面给出的代码。

(1) a[rp] > x，a[lp] < x

假如给出一个数组数据如下：
初始数组
如果按照这个条件执行代码，这里的左右两个指针根本不会发生移动，导致排序陷入死循环，最终得不到排序结果。

(2) a[rp] >= x，a[lp] < x

假如给出一个数组数据如下，并且左右指针已经完成一轮移动了，它们此时的位置如下：
初始数组
接下来就是交换两个指针指向的值，交换后：
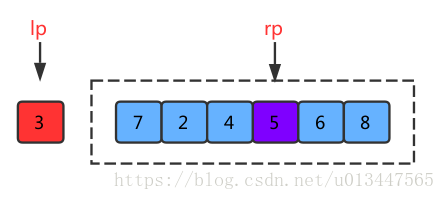
交换大小值
由于排序还没完成，紧接着进行下一轮移动，先移动右指针：
基准值位置丢失
到这里，问题已经出来了。可以看到，基准值的位置丢失了，也就是说最终无法确定基准值的位置了（也就是所在的数组索引）。我们都知道，partSort 方法最终需要返回基准值的最终位置，然后才能正确地分成一大一小的两部分进行递归排序。但是此时却把基准值的位置给弄丢了，那最后也就无法拿到正确的分割点，导致排序失败。