证明不是哈密顿图的几种方法归纳总结

    相关定义：设G=<V,E>为一图(无向的或有向的).G中经过每个顶点一次且仅一次的通路称作哈密顿通路；G中经过每    个顶点一次且仅一次的回路称作哈密顿回路；若G中存在哈密顿回路，则称G为哈密顿图。

   (只是根据自己的体会总结的，因为是初学者，有不完善的地方，欢迎指正。)

   首先要证明不是哈密顿图，则要破坏哈密顿图存在的必要条件，证明其必要条件不成立即可。（因为如果无向图G为哈密顿图，则……，其中……为其必要条件，若不满足……，则该图不是哈密顿图）。

 1.若无向图G=<V,E>为哈密顿图，V1是V的任意真子集，则p(G-V1)<=|V1|，其中，p(G-V1)为从G中删除V1后所得图     的连通分支数。

2.若无向图G=<V,E>为哈密顿图，则图G中无割点。

3.若无向图G=<V,E>为哈密顿图，且图G为完全二部图Kr,s，则r=s。

4.若无向图G=<V,E>为哈密顿图，则图G一定存在一条哈密顿回路。（标号法）

5.若无向图G=<V,E>为哈密顿图，则图G必为连通图。

6.若无向图G=<V,E>为哈密顿图，则图G中边数m必须大于等于顶点数n。

7.若无向图G=<V,E>为哈密顿图，且G中存在2度顶点v，则与v关联的两条边ei，ej必须在G中的任何哈密顿回路上。

8.若无向图G=<V,E>为哈密顿图，则G中必须必须在每条哈密顿回路中出现的边，不能构成边数小于n的初级回路。

9.若无向图G=<V,E>为哈密顿图，则图G的闭包C(G)为哈密顿图。

(划线部分为证明中比较常用的，还有很多必要条件不一一列举了)

标记法：

任取一结点如v1,用A标记，所有与它邻接的结点标B。继续不断地用A标记所有与B邻接的结点，用B标记所有与A邻接的结点，直到图中的所有结点全部标记完毕。如果图中有一条汉密尔顿路，则必交替通过结点A和B。因此或者结点A和B数目一样，或者两者相差1个。（A与B数目一样则存在哈密顿回路，|A-B|=1则存在哈密顿通路）。

但是，遇到让判断是不是哈密顿图时，不要盲目地以为不是哈密顿图，从而直接利用上述各种证明方法来证明不是哈密顿图，要仔细看图，利用哈密顿图存在的充分条件判断是否是哈密顿图。

例如：

这是一个汉密尔顿图，其汉密尔顿圈为chfigjdeabc。

 哈密尔顿圈为abcdhijgfea。

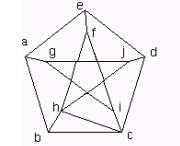
参考文献：离散数学（第二版）屈婉玲 耿素云 张立昂 编著 清华大学出版社2008.02第二版