hdu4753 状态压缩dp博弈（记忆化搜索写法）

http://acm.hdu.edu.cn/showproblem.php?pid=4753

Problem Description

　　　There is a 3 by 3 grid and each vertex is assigned a number.


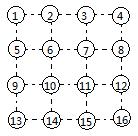
　　　It looks like JiuGongGe, but they are different, for we are not going to fill the cell but the edge. For instance,


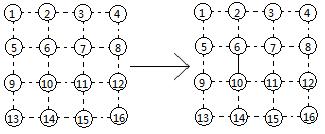
adding edge 6 –> 10
　　　The rule of this game is that each player takes turns to add an edge. You will get one point if the edge you just added, together with edges already added before, forms a new square (only square of size 1 is considered). Of course, you get two points if that edge forms two squares. Notice that an edge can be added only once.


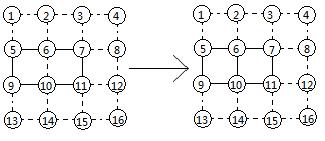
forming two squares to get two points
　　Tom200 and Jerry404 is playing this little game, and have played n rounds when Fishhead comes in. Fishhead wants to know who will be the winner. Can you help him? Assume that Tom200 and Jerry404 are clever enough to make optimal decisions in each round. Every Game starts from Tom200.

 

Input

　　The first line of the input contains a single integer T (T <= 100), the number of test cases.
　　For each case, the first line contains an integers n (12 <= n <= 24), which means they have taken total n rounds in turn. Next n lines each contains two integers a, b (a, b <= 16) representing the two endpoints of the edge.

 

Output

　　For each case output one line "Case #X: ", representing the Xth case, starting from 1. If Tom200 wins, print "Tom200" on one line, print "Jerry404" otherwise.

 

Sample Input

  
  

   
   1
15
1 2
1 5
2 6
5 9
6 10
9 10
5 6
2 3
3 7
7 11
10 11
3 4
6 7
7 8
4 8
  
  

 

Sample Output

  
  

   
   Case #1: Tom200

   
   

    
    

     
     Hint
    
    
　　In case 1, Tom200 gets two points when she add edge 5 -> 6, two points in edge 6 -> 7, one point in 4 -> 8.
   
   
  
  

/**
hdu4753 状态压缩dp博弈（记忆化搜索写法）
题目大意:为一个3*3的棋盘连边（如图所示）加上当前边后多了几个格子四条边都被填上了，就得几分，现在tom和jerry交替填边，总是tom先，
          现在已经填了n条边了，问剩下的边二者都采取最优的策略，谁会赢
解题思路：由于未知的边最多只有12条，我们可以采取状态压缩，用搜索的方式写
注意：不可以直接压24位，会爆内存的
*/
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <iostream>
using namespace std;
int mp[24][24];///给每条边进行编号
int vis[25];///标记是否已经访问过该边
int dp[(1<<13)+3],cnt,x[25];
int tom,jerry,n;
int circle[9][4]={///对应的9个格子各自的四条边
1,4,5,8,
2,5,6,9,
3,6,7,10,
8,11,12,15,
9,12,13,16,
10,13,14,17,
15,18,19,22,
16,19,20,23,
17,20,21,24
};
void init()
{
    memset(mp,0,sizeof(mp));
    mp[1][2]=1,mp[2][3]=2,mp[3][4]=3;
    mp[1][5]=4,mp[2][6]=5,mp[3][7]=6,mp[4][8]=7;
    mp[5][6]=8,mp[6][7]=9,mp[7][8]=10;
    mp[5][9]=11,mp[6][10]=12,mp[7][11]=13,mp[8][12]=14;
    mp[9][10]=15,mp[10][11]=16,mp[11][12]=17;
    mp[9][13]=18,mp[10][14]=19,mp[11][15]=20,mp[12][16]=21;
    mp[13][14]=22,mp[14][15]=23,mp[15][16]=24;
}
int judge()
{
    int sum=0;
    for(int i=0;i<9;i++)
    {
        if(vis[circle[i][0]]&&vis[circle[i][1]]&&vis[circle[i][2]]&&vis[circle[i][3]])
             sum++;
    }
    return sum;
}

int ok(int ste,int k)
{
    int vv[25];
    memset(vv,0,sizeof(vv));
    for(int i=0;i<=cnt;i++)
    {
        if(ste&(1<<i))
            vv[x[i]]=1;
    }
    int s1=0,s2=0;
    for(int i=0;i<9;i++)
    {
        if((vis[circle[i][0]]||vv[circle[i][0]])&&(vis[circle[i][1]]||vv[circle[i][1]])&&(vis[circle[i][2]]||vv[circle[i][2]])&&(vis[circle[i][3]]||vv[circle[i][3]]))
            s1++;
    }
    vv[x[k]]=1;
    for(int i=0;i<9;i++)
    {
        if((vis[circle[i][0]]||vv[circle[i][0]])&&(vis[circle[i][1]]||vv[circle[i][1]])&&(vis[circle[i][2]]||vv[circle[i][2]])&&(vis[circle[i][3]]||vv[circle[i][3]]))
            s2++;
    }
    return s2-s1;
}

int dfs(int ste,int k)
{
    if(dp[ste]!=-1)return dp[ste];
    int maxx=0;
    for(int i=0;i<=cnt;i++)
    {
        int s=1<<i;
        if((s&ste)==0)
        {
            s=ste|s;
            int t=ok(ste,i);
            int sum=dfs(s,k-t);
            if(k-sum>maxx)
                maxx=k-sum;
        }
    }
    return dp[ste]=maxx;
}
int main()
{
    int T,tt=0;
    scanf("%d",&T);
    init();
    while(T--)
    {
        memset(vis,0,sizeof(vis));
        scanf("%d",&n);
        tom=0,jerry=0;
        int s=0,ste=0;
        for(int i=0;i<n;i++)
        {
            int x,y;
            scanf("%d%d",&x,&y);
            if(x>y)swap(x,y);
            vis[mp[x][y]]=1;
            int s1=judge();
            if(i&1)
            {
                jerry+=(s1-s);
            }
            else
            {
                tom+=(s1-s);
            }
            s=s1;
           /// printf("(%d %d)\n",tom,jerry);
        }
        cnt=-1;
        for(int i=1;i<=24;i++)
        {
            if(!vis[i]) x[++cnt]=i;
        }
        s=9-judge();
        memset(dp,-1,sizeof(dp));
        int num=dfs(0,s);
        printf("Case #%d: ",++tt);
        if((n&1)==0)
        {
            if(tom+num>jerry+s-num)
                printf("Tom200\n");
            else
                printf("Jerry404\n");
        }
        else
        {
            if(tom+s-num>jerry+num)
                printf("Tom200\n");
            else
                printf("Jerry404\n");
        }
    }
    return 0;
}