【重庆四校联考】电路图A-巴蜀T1（组合数学）

电路图A

时间限制 : 1s 空间限制 : 256MB 
(A.cpp/c/pas)

【问题描述】

nodgd 要画一个电路图。 
这是一个很简单的电路图，所有的元件都是串联关系，从整体来看就是一个环状的结构。画电路图有很多要求，nodgd 为了画得好看就又添加了一些额外的要求。所有要求归结起来有以下几点： 
1. 这个环状电路上有n个双端电路元件（即每个电路元件有两个 连接导线的接头），其中只有一个直流电源；为了本题方便， 
其他 n − 1 个元件都是一模一样的电阻。 
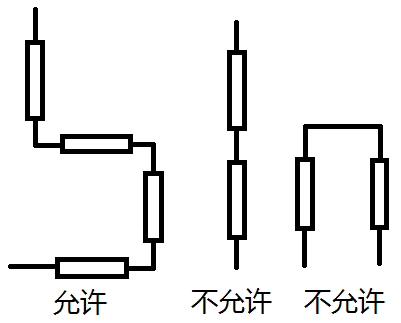
2. 电流在电路图中每经过一个元件，就必须拐一个90°的弯；没有经过元件时不允许拐弯。参考右图。 
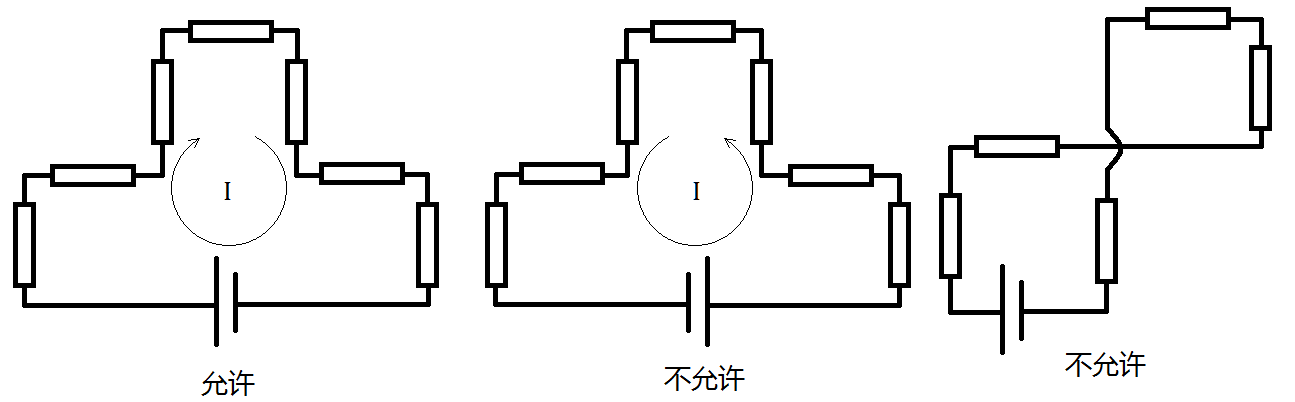
3. 从电路图整体上观察，电流沿顺时针方向流动，且电路不能自交。参考下图。 

 
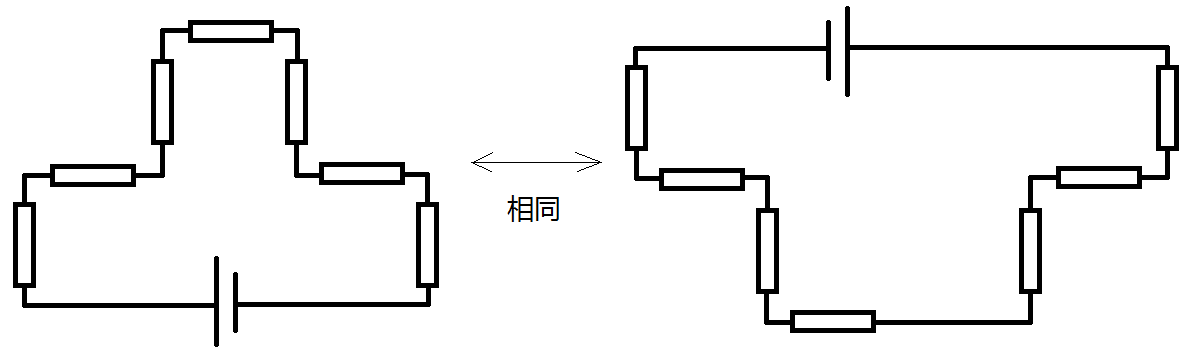
4. 如果一个符合题意的电路图，可以通过整体旋转一定的角度，再适当调整图中导线的长度，得到另外一个符合题意的电路图，则这两个电路图是相同的。参考下图。 

那么问题来了，nodgd想知道有多少种不同的电路图，以及有多少种不同的美观电路图。由于两个问题的答案都可能很大，请mod 1,000,000,007输出结果。 
【输入格式】 
输入文件A.in。 
输入文件第一行包含一个正整数n，表示包含电源在内的电路元件的总数量。 
【输出格式】 
输出文件A.out。 
输出文件第一行包含一个整数，表示不同的电路图数量mod 1,000,000,007的结果。 
第二行包含一个整数，表示不同的美观电路图数量mod 1,000,000,007的结果。 
【输入输出样例1】 
A.in 
6 
A.out 
6 
6 
见分发给选手的压缩文件中的sample\A1.in和sample\A1.ans。 
【输入输出样例1说明】
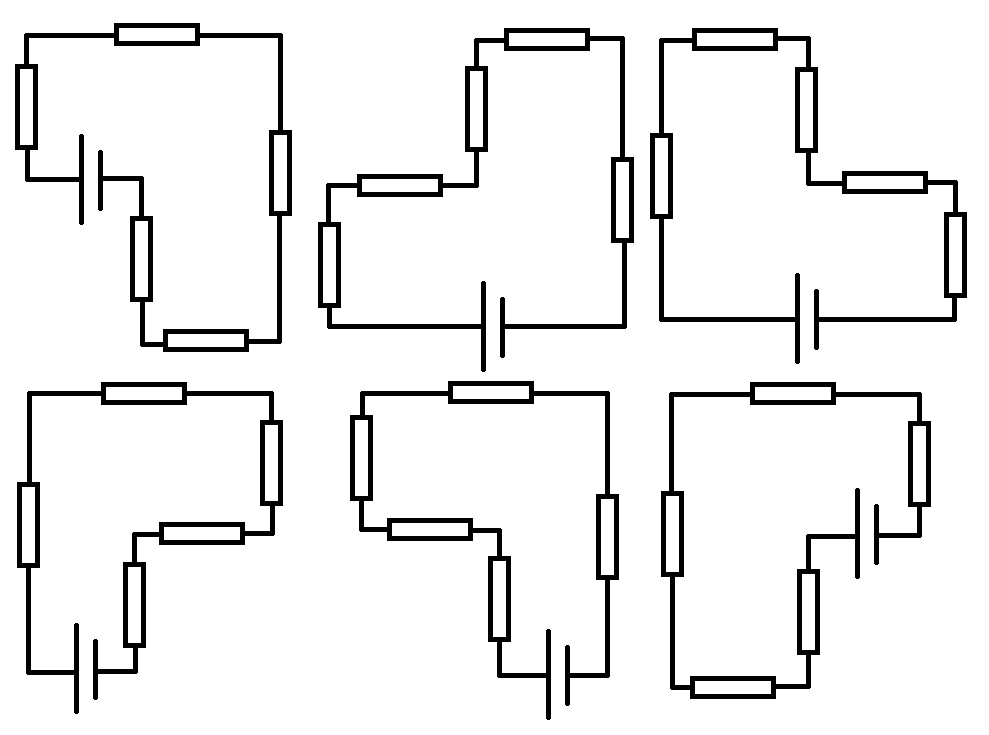
可以有如下几种电路图，电路图数量是6，所以输出文件第一行输出一个整数6； 
容易发现，这6个电路图都是美观的电路图，所以第二行也输出一个整数6。 

【输入输出样例2】 
A.in 
10 
A.out 
120 
50

解题报告：

%%%JJDS nodgd

我死也不信NOIP第一题那么难

把顺时针方向看为正方向

首先由于题目中说每两个元件之间必须拐90度，因此电路图可以表示为一个长度为n的L和R组成的序列，其中L代表一个左拐，R代表一个右拐

因为电路图最后要拐360度回到起点，所以L和R的数量l，r有这么一个关系：   l = r-4

接下来就成了不同排列的序列个数问题，转换成计算n中选(n-4)/2个元素的组合数，使用公式Cmn=n!/(m!(n-m)!)

（本来可以用二分数列来O(logn)求阶乘，这里博主懒就不写了。。。）算组合数+取模运算为了应对有个小技巧，模除法需要转换为乘逆元，求逆元可以用扩展欧几里得，这里的p是质数吗，也可以用logp的费马小定理（a*a^(p-2) 同余 1 (mod p)  ，所以a^(p-2)为a逆元，用快速幂log p求得），下面的代码使用费马小定理。

问题一就解决了

问题二：

因为从内部任何一点都可以看到所有元件，所以不能有向内的矩形凸起，也就是说序列中不能有连续两个L出现

为了计算这个限制下的组合方案数，考虑在r个R中插入l个L

因为这个图转化为的序列是首尾相接的环，所以位置1和位置n不能同为L，分类讨论之后可以得到这个答案等于组合数之差（具体见代码），

代码

#include<cstdio>
typedef long long LL;
const LL MOD=1000000007;
LL advpow(LL a,LL b){
    LL ret=1;
    while(b){
        if(b&1)ret*=a,ret%=MOD;
        a*=a;
        a%=MOD;
        b>>=1;
    }
    return ret;
}
LL moddiv(LL a,LL b){
    return (a*advpow(b,MOD-2))%MOD;
}
LL getC(LL a,LL b){
    LL fac1=1,fac2=1;
    for(int i=a+1;i<=b;i++)
        fac1*=i,fac1%=MOD;
    for(int i=b-a;i;i--)
        fac2*=i,fac2%=MOD;
    //printf("fc1:%I64d fc2:%I64d\n",fac1,fac2);
    return moddiv(fac1,fac2);
}
int main(){
    int n;
    scanf("%d",&n);
    int k=(n-4)/2;
    LL p=getC((n+4)/2,n);
    LL ans2=(2LL*getC(k,n-k)-getC(k,n-k-1))%MOD;
    if(ans2<0)ans2+=MOD;
    printf("%lld\n",p);
    printf("%lld\n",ans2);
}