Unique Paths

ifwantwill

于 2014-04-15 04:09:07 发布

阅读量294

点赞数

分类专栏： Leetcode

本文链接：https://blog.csdn.net/u013797029/article/details/23725345

版权

Leetcode 专栏收录该内容

132 篇文章 0 订阅

订阅专栏

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

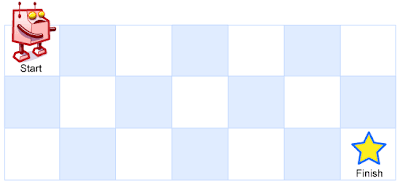
Above is a 3 x 7 grid. How many possible unique paths are there?

Note: m and n will be at most 100.

如果直接递归，通不过大数据测试，先贴一个自己实现的dp

class Solution
{
public:
		 int uniquePaths(int m, int n)
		{
			if (m == 0 || n == 0) return 0;
			vector<vector<int> >dp(m + 1, vector<int> (n + 1, 0));
			dp[1][1] = 1;
			if (m > 1)
				dp[2][1] = 1;
			if (n > 1)
				dp[1][2] = 1;
			judge(m, n, dp);			
			return dp[m][n];
		}
		int judge(int m, int n, vector<vector<int> >& dp)
		{
			if (dp[m][n] > 0)
				return dp[m][n];
			int hor = 0;
			int ver = 0;
			if (m > 1)
				hor = dp[m - 1][n] > 0 ? dp[m - 1][n] : judge(m - 1, n, dp);
			if (n > 1)
				ver = dp[m][n - 1] > 0 ? dp[m][n - 1] : judge(m, n - 1, dp);
			dp[m][n] = hor + ver;
			return dp[m][n];
		}
};

再贴一个来自别人的答案巧妙的dp

class Solution
{
public:
		int uniquePaths(int m, int n)
	{
		vector<int> maxV(n,0);  
		maxV[0]=1;  
		for(int i =0; i< m; i++)  
		{  
			for(int j =1; j<n; j++)  
			{  
				maxV[j] = maxV[j-1] + maxV[j];  
			}  
		}  
		return maxV[n-1]; 
	}
};