3D数学系列之——从“蒙的挺准”到“蒙的真准”解密蒙特卡洛积分！

1、前言

  在学习3D数学的过程中，或者说在学习游戏开发、引擎开发、渲染器开发、Shader开发的过程中，对大家来说，当然也包括我，数学是一道必须要迈过的坎，而无论你有多么头疼。

  目前市面上所见3D数学类的书籍，其内容还是主要集中在3D的线性代数部分，即向量和矩阵的理论及运用上，这部分内容其实如果有初高中的牢固的数学的基础的话，理解和掌握是不难的。但是在真正的渲染编程的过程中，仅仅有线性代数的知识是远远不够的，还需要牢固的掌握微积分和概率论方面的知识，其中尤其是微积分知识，更是现代基于全物理仿真的渲染过程中必备的硬核技能之一。然而这一部分的内容就鲜见于各种3D数学类书籍的内容中。

  本章就带大家简单补一下这部分的知识，并重点介绍在PBR光照理论中非常非常重要的蒙特卡洛积分的知识，目的就是让大家彻底搞明白它的理论以及它为啥对计算这么重要。

2、积分概念简单回顾

  其实一开始的时候，我也是没有搞明白蒙特卡洛积分到底是啥，而且我几乎翻遍了我手头所有能找到的资料以及网上的资料后，都感到比较失望，这些资料要不是没有介绍这个重要的概念，要不就是简单的说是基于概率的积分就了事了。究竟为啥一个积分的运算会牵扯到概率，更是让我一脸懵逼。

  既然它叫蒙特卡洛积分，那么首先让我们来回顾一下究竟啥是积分，当然纯数学理论化的积分概念大家可以去翻书慢慢啃了。本文目的是为了让大家能够彻底理解蒙特卡洛积分的原理，因此可能会用不太严格，或者说比较形象的说法。

  那么积分在平面上就是计算某段曲线下与x轴及两个平行于y轴的直线所围成的面积大小，计算的基本过程是曲线在某个x处的值，乘以对应的包围这个x形成的一个极小分段，得到一个细长条的面积，这很像一根“面条”（忽略其厚度），并使其长度等于f(x)，然后再累加这些面积得到整个图形的面积，也就是把无数“面条”一根根并排放起来然后形成一个面积的大小。如下图所示：

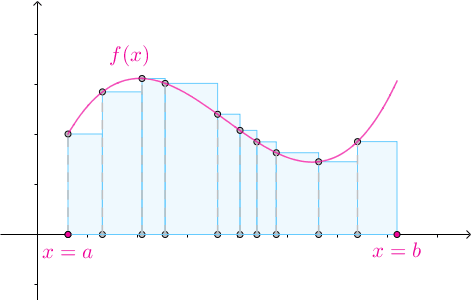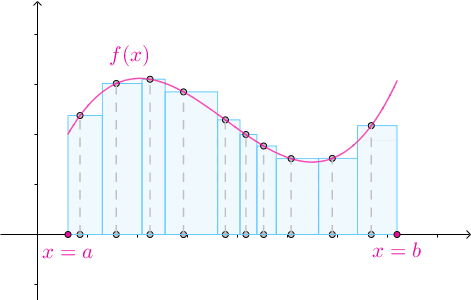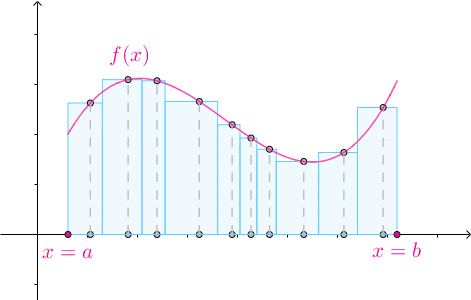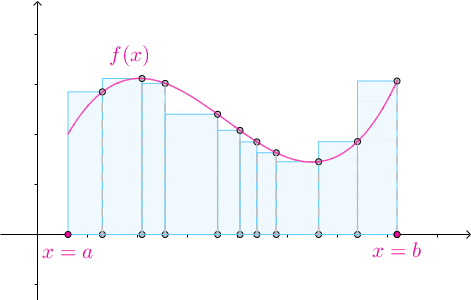
  对于3D立体的情况，积分就是计算曲面和垂直于轴的平面围成的体积，计算过程也是通过曲面在某个段围成的面积乘以一个极小的高得到一张“煎饼”似的体积大小，然后再累加得到整个曲面围成的体积的大小，可以想象为近乎无数的“煎饼”摞起来后的体积。如下图所示：

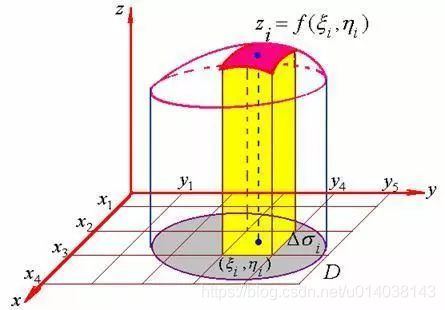
  以上是定积分的概念，当去除平行于轴直线或垂直于轴的平面的限制之后，那积分计算出来的就是一个函数称为原函数或反导数，也就是不定积分。

  一般情况下定积分的公式如下（仅列举单变量和双变量的情形）：
$$\begin{gathered} S={\int }_a^{b}f(x)dx \\ V={\int }_{y_0}^{y_n}{\int }_{x_0}^{x_n}f(x,y)dydx \end{gathered}$$
  近似公式如下：
$$\begin{gathered} S\approx \sum _{\Delta x\to 0}f(x)\Delta x \\ V\approx \sum _{\Delta s\to 0}f(x,y)\Delta s(一般取\Delta s=\Delta y\times \Delta x) \end{gathered}$$
  当然上面的近似公式中，第一个与之前举的“面条”的例子比较类似，无非就是说要让“面条”足够窄，并且忽略其厚度，当然你可以想象成“面条”被扯成了“龙须面”，甚至是“头发丝”，只是其数量必须要密集填满a-b的空间（如果有兴趣你可以拔自己的一把头发摆放一下试试）。而第二个近似与之前说的“摊煎饼”有点差别，它本质的意思仍然是用截面积无穷小的“面条”来紧密竖排成一捆，这时不能忽略面条横截面积的任何一个维度，而其长度就等于f(x,y)。

  近似公式的图形化理解如下：

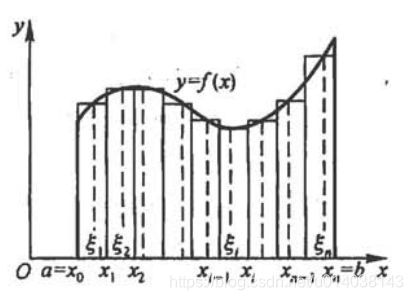
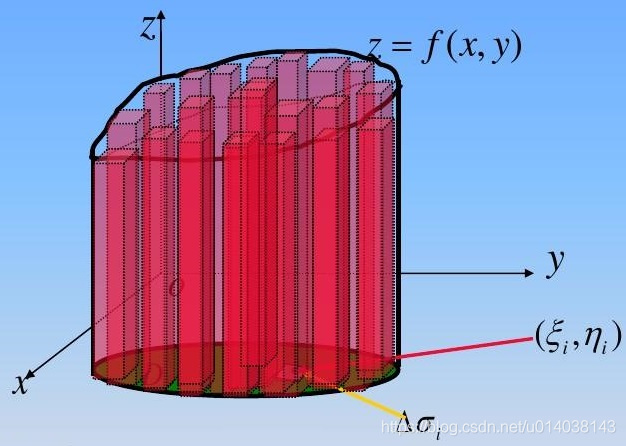
  ok，到这里只是带大家复习了一下积分的含义，其实说白了就是为了“求和”，即小窄长面积累加成一个大面积，或者小窄长条累加长一个大的体积。

  最后需要回顾的就是定积分与不定积分间重要的“牛顿-莱布尼茨公式”：
$${\int }_a^{b}f(x)dx=F(b)-F(a)其中F(x)是f(x)的原函数，或者说F^{\prime }(x)=f(x)$$
  这个公式也提示说，如果有办法求得一个函数的原函数，那么定积分的计算就可以用其原函数在区间端点处的两个值求差即可得到。

3、积分在程序计算上的困难

  通常计算机中能够轻松计算的一般是求数值解的定积分：比如输入一个函数的表达式f(x)，给定区间[a,b]两点，求定积分，此时将b-a的长度n等分，每个等分取左端点xi，其中x0=a，xi=a + (b-a)/n，计算f(xi)，再乘以(b-a)/n，累加每个乘积结果就得到了定积分的近似值，并且随着n的不断增大，结果不断趋近于定积分的精确解。如下示例程序演示了“矩形法”求定积分的计算过程：

double f( double x ) /*某个函数*/
{
    return exp( 3 * x ) + pow( x, 7 );
}
double Integral( double a, double b, long int n ) /*矩形法*/
{
    double sum = 0;
    double x = a;
    double delta = ( b - a ) / n;
    for ( long i = 1; i <= n; i++ )
    {
        x += delta;
        sum += f(x);
    }
    sum = sum * delta;
    return sum;
}

  当然现代的一些专业数学软件也可以进行完全基于公式（解析式）的不定积分的计算。比如下面的Matlab程序示例就计算了两个函数的不定积分(Matlab中求积分函数为int)：

syms x;
int(-2*x/(1 + x^2)^2)
The result is:
ans =
1/(x^2 + 1)

syms x z;
int(x/(1 + z^2), z)
The result is:
ans =
x*atan(z)

  所谓理想很丰满，现实却很骨感。首先并不是所有的解析式都能通过公式法来解出其不定积分的解析解，而且很多时候即使专业的数学软件解出来的解析解也不一定是人类能够理解或验证的。其次，有些函数，尤其是来源于现实中的函数，有时候甚至连其表达式都很难得到，这时候往往得到的可能是该函数在某个坐标点上或者某个时间点上的一些离散的值。

  比如，土地测绘人员在一定范围内测得一块土地上间隔一定距离的点的高度（大家应该见过测绘系的同学天天扛着高度计和标尺满世界到处奔波测量的样子）。现在假设需要平整这块土地来建房子，在工程上就需要计算出需要挖多少土方量（也就是多少立方米的土），以便进一步计算需要消耗多少费用和时间。这时土地表面形成的曲面，其解析式几乎是无法得到的，即使得到也只是近似表达式，同时还可能无法简单的对其求原函数。

  这些都是利用计算机程序来计算定积分值时的巨大困难。或者可以这样来理解，基于求原函数，或者纯数值解法所能计算的定积分问题，只是现实中定积分问题中的一小部分。这也可以用二八原理来想象，即现实中只有大约20%（可能远小于这个估值）的定积分问题可以通过前述的方法来解决，且先不论方法本身的难易程度，而另外80%的问题是没法用前述方法解决的。

4、蒙特卡洛积分

  对于上述的那些不太好积分的情况，聪明的人类尤其是工程师们就想出了很多近似的方法，其中本文讲述的重点蒙特卡洛积分法就是其中的一种。

  当然对这些近似方法，数学家往往会采取比较保守的态度，顶多就是给出一种结果准确度的证明或简单的说明就了事了（即常说的级数收敛还是不收敛，因为大多数积分近似方法展开后就是级数。）然后基本就不理会了，所以就很难在比较正统的数学书中找到它们的踪迹，这也是我翻了好多数学书，却不见蒙特卡洛积分法踪影的原因。然后另一方面，物理学家、工程师、计算机人员等对这些近似方法却情有独钟，甚至于运用到数学家们都有点看不下去的程度。说白了这些近似方法在非数学家圈子能有这么广泛的运用，完全是因为它们在计算上实在是太方便了。

  这里插播一个有名的笑话，就是关于概率统计的正太分布公式的：物理学家们认为正太分布公式是数学家们在概率统计方面证明出来的最有用的一个公式，而数学家们则认为正太分布公式是物理学家们总结出的最优美的经验方程！

  ok，如果你看明白了，并且笑完了，那就继续让我们来看看啥叫蒙特卡洛积分法。

  一开始，在我看到蒙特卡洛积分法居然和概率有关系的时候，然后在各种数学资料里都找不到它的时候，我一度认为它可能就是一个“蒙的挺准”的经验公式啥的。直到有一天我翻出了珍藏已久的《托马斯微积分》居然在目录中看到了蒙特卡洛积分，那当然就是啥也不用唠，就是一顿撸，看完之后我就哈哈大笑，原来这就是个“蒙的真准”积分法。那么究竟是怎么回事呢？

  大家一起看下图：

  假设图中红色曲线与x=0（y轴，实际不一定非要y轴对齐，可左可右）、x=L围成了一个灰色的图形，现在要计算灰色部分的面积。虽然这个曲线可能是正弦曲线，但在这里想象它是随意的一条曲线（画图实在太麻烦了，先用这么个曲线顶一下），并且没法求其原函数F(x)。

  此时假设未知函数f(x)有上界M，这时L和M围成了一个包围图形的矩形，即图中虚线围成的部分，其面积显然为L*M。现实中总是可以得到这样的M与L，可以取M为一组f(x)的最大值，L即待求定积分区间的b值或（b-a）的值（本例中a=0）。接着对整个矩形内随机的取点，如图中红点和黑点，都是随机取的，颜色只是为了区分点在灰色部分，还是没在灰色部分（但一定在矩形中）。

  这个过程，就像在著名动画片《花园宝宝》里的著名场景一样：让我们一起来数小点点，一个小点点、两个小点点、三个小点点、$\cdots \cdots$

  这些点是否在灰色部分，很好判断，即取该点的x值，然后计算或取得f(x)的值，判断点的y值是否小于这个值，如果小于，那么点一定位于灰色部分。

  这里需要提醒大家的是，如果f(x)是解析式，那么求其极值是很方便的，一般取导数及二次导数就可以判定了，并且求导数总是比求原函数要方便很多。如果是离散值，那么取其中一个最大值即可。

  另外，如果f(x)或x中有负值，那就需要首先取绝对值最大的值，然后以x=0或y=0为分界线，分不同的象限（3D中是卦限）取有向面积再求和即可，即位于1、3象限的面积为正值，位于2、4象限的面积为负值，然后求和。

  这样只要保证取点的过程足够随机（看到这里，对！你想的没错，这其实就是取一系列随机的x值和y值，计算时用伪随机系列产生，当然超出矩形范围的点就丢弃，或者用算法保证产生的点只在矩形范围内），那么这些点最终落在灰色部分或矩形中非灰色部分的概率只与这两部分面积的大小有关，这很好理解（这是关键！），面积大的部分随机点落进去的概率肯定大一些。

  最终落在灰色部分的点与面积有下面的概率公式：

$$\begin{gathered} \frac{灰色部分中点数}{总的点数}\approx \frac{灰色部分面积}{矩形面积} \\ \Rightarrow 灰色部分面积\approx 矩形面积\times \frac{灰色部分中点数}{总的点数} \end{gathered}$$

  而灰色部分面积就是要求的定积分值！

  ok，以上就是蒙特卡洛积分法全部核心的秘密了，即好理解也好计算，果然是“蒙的挺准”！并且其中大矩形的面积很容易就确定了，剩下的就是随机产生足够多的点即可。当然按照数学家的说法，这个方法实在是收敛的太慢了，虽然有“大数定律”（简单的理解为随机变量的统计样本均值在足够多的情况下无限趋近于其真实概率值，在这里就是 “灰色部分中点数/总点数”趋近于面积的比值）保证其结果一定是收敛的。但是这对计算机来说毫无压力，无非就是想尽一切办法产生足够多的点即可，当然伪随机数的“质量”也要足够好！对于精度要求不高的场合，这是一个非常有效且简单的方法。

  对于离散f(x)值的情形，仅需要对每个x值随机产生一个y值即可，但这要求采样的(x,f(x))值对也要足够多，同时假定f(x)值在极小的区间上没有太多突变，也既数学上说的需要足够的“连续性”，如果有突变，可能需要使值对进行分组，即常说的分段积分法。不过幸运的是，现实中大多数情况下，(x,f(x))值对的“连续性”是足够好的。当然“天气变化”或“股票变化”以及人类捉摸不定的情绪变化等情形除外！

  同时，除了这里讨论的2D平面图形的情形外，蒙特卡洛积分法可以很方便的推广到3D体积计算的情形，或更高维的情形。3D情形下，无非就是需要假定一个包围整个3D几何体的，可以方便求其体积的规则包围几何体即可，比如立方体、长方体、球体、锥体、棱柱、棱台等等。并且产生足够多的3D随机点即可。

  在实际中，3D渲染中的PBR过程中，就是规定包围体为一个半球体，然后求所有可能的入射光线产生的能量的和（积分）。具体的应用在讲到PBR渲染时再做详细分析。希望看到这里你已经完全理解了蒙特卡洛积分法的全部意义！

5、一些扩展应用

  之前就说过，非数学家通常会将这些近似的计算方法运用到“令人发指”的地步，那么作为简单又好用的蒙特卡洛积分当然也就“难逃魔掌”了。在刚才的公式中：

$$灰色部分面积\approx 矩形面积\times \frac{灰色部分中点数}{总的点数}$$

  其中乘号右边的部分，其实就是一个概率值，既然是概率值很多时候其实是可以估计一个近似值作为经验值，那么最终求定积分的问题，就变成了一个简单的乘法运算：
$$灰色部分面积\approx 矩形面积\times P（P为点落在灰色部分的概率）$$
  比如下面的计算是我们很熟悉的：

  其中阴影部分三角形，可以大概看出占用了矩阵框中的1/2，或者说点出现在阴影中的概率大约是0.5，所以最终这个三角形的面积=1/2*a*b！这与小学初中时老师们想尽一切办法想让我们理解的三角形面积公式是完全一致的，或者说三角形面积公式也是蒙特卡洛积分的一个自然结果，只是它是完全建立在概率的基础上。此时根本不用关心什么底啊、高啊之类比较饶头的各种概念！

  当然上面的公式还可以反过来用，即可以让图形灰色部分完全包围一个矩形，然后知道了点落在矩形中的概率，如下图：

  根据图示，圆内矩形面积已知=a*b，然后估计点落在矩形中的概率约等于0.80 , 此时整个圆的面积就约等于=a*b/0.80=1.25*a*b，当然这完全是一种估算，在精度要求不高的情形下，其计算即快又简单。这种情况下，当矩形在图形内时，概率就是指点落在矩形内的概率，此时概率要取倒数来计算外接图形的面积。当然图形中画个圆的意思只是一个特例，现实中，总可以在任意不规则图形内或外绘制一个合适大小的矩形，然后估计概率，再估算出整个图形的面积。掌握了这一招，大家可以试着在地图上估计下贝加尔湖的面积，当然如果你的概率“蒙的不够准”，那么就蒙上眼睛在地图上点小点吧，最后你可以通过数小点完成“蒙的真准”的计算！