机器学习的基本介绍以及对线性问题求解问题的基本阐述
1、机器学习的用途
1). 用来进行数据挖掘
2). 让机器进行自我学习
3). 能对用户进行个性化定制的应用程序
4). 了解人类大脑的运行机制
2、什么是机器学习
Arthor Samuel的定义：是在没有对机器进行明确的编程的情况下让机器具有自主学习的能力。
3、学习算法的分类
学习算法主要分为两大类，监督学习算法和非监督学习算法。
监督学习算法就是明确告诉一个程序接下来该如何进行操作，非监督学习就是让机器自己学习该如何进行下一步操作。例如回归问题与分类问题。
非监督学习算法是给一个程序一个数据集合，让程序自己判断，自己在数据中找到规律。例如，聚类算法。
4、监督学习之回归问题
1)线性回归问题：预测函数的形式像y=d+ax,其中只有x是变量，d和a可以通过对数据进行拟合而获得。
具体方式是取得恰当的d和a， 使得
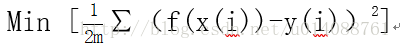
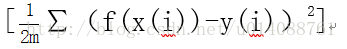
2)梯度下降算法。计算方法是
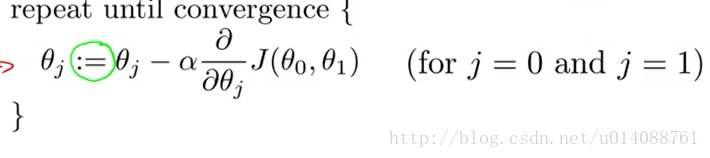
3）多元线性回归问题：y=x0+θ1x1+θ2x2+….+θnxn,用矩阵来表达就是y=A*X T,其中，X=
{x0x1x2x3...xn}
{
x
0
x
1
x
2
x
3
.
.
.
x
n
}
A=
⎧⎩⎨⎪⎪⎪⎪⎪⎪//x01...1feature1a11...an1feature2a12...an2feature3...a13......an3...featurena1nann⎫⎭⎬⎪⎪⎪⎪⎪⎪
{
/
/
x
0
f
e
a
t
u
r
e
1
f
e
a
t
u
r
e
2
f
e
a
t
u
r
e
3...
f
e
a
t
u
r
e
n
1
a
11
a
12
a
13...
a
1
n
.
.
.
.
.
.
.
.
.
.
.
.
1
a
n
1
a
n
2
a
n
3...
a
n
n
}
Tip1 :单一变量的高次问题可以通过设置不同的变量与变量的不同次方与它相对应从而可以将其降低为线性回归问题，但是得注意他们的取值范围应该相差不是很大。
Tip2:注意特征的选取，不同的特征选取对我们的算法性能以及计算的复杂度的影响是很大的。
多元问题的梯度下降算法：
；
4）正规方程法：通过建立方程组再使用求导来求极值的方法得到最终的确切参数
600
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
