选择题快速求解AOE网的关键路径

#引言

求解AOE网关键路径时，书上的方法为先从源点到汇点求解事件最早发生时间ve，再从汇点到源点求解事件最迟发生时间vl，再利用ve和vl求解每个活动的最早开始时间e(i)和最迟开始时间l(i)，e(i)和l(i)相等的活动则为关键活动，关键活动组成的从源点到汇点的路径即为关键路径。

王道的书上在AOE的部分，备注了一小行话：“如果这是一道选择题，根据上述求ve()的过程就已经能知道关键路径。”，但并没有展开讲如何确定。本文就补充说明一下。

#求法

这里直接举例给出求法

如下AOE图

我们从V1开始依次求解事件的最早发生时间ve，前三个顶点答案很显然，求得如下

	V1	V2	V3	V4	V5	V6
ve()	0	3	2

在求解V4的时候，需要对两条路径进行比较，即ve(4)=Max{ve(2)+a3,ve(3)+a5}=Max{5,6}，显然选取的是a5这条路径。

这意味着a3这条路径对V4来讲是"冗余的"，或者说因为a5的存在，它有可以改变的空间。也就是a3一定不是关键路径。我们可以叉掉它。

按照以上思路，我们完成ve()的求解，并叉掉那些比较时被比下去的路径。

最后得到：

直观一点，我们把这些路径都去掉：

上图中，V1是源点，V6是汇点，完成工程意味着 V1到V6的一条路径，而去掉“不关键”的路径（活动边）后 还可以走通的路径就是关键路径。

即上图中的(V1,V3,V4,V6)或者说(a2,a5,a7)

（注：a1和a4虽然保留在图中，但并不是关键活动，因为他们不在关键路径上）

---

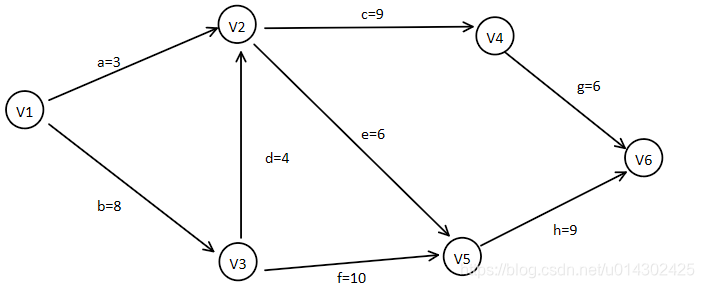
再举个多条关键路径情况的例子，我们从V1开始依次计算ve()。

	V1	V2	V3	V4	V5	V6
ve()	0	Max{3,ve(3)+4}	8

 

计算到V2时，比较两条路径，淘汰路径a，ve(2)=12

	V1	V2	V3	V4	V5	V6
ve()	0	12	8	21	Max{ve(3)+10,ve(2)+6}

计算到V5时，两条路径消耗是相同的！这时候两条路径都保留下来，他们都有可能成为关键路径。

	V1	V2	V3	V4	V5	V6
ve()	0	12	8	21	18	Max{ve(5)+9,ve(4)+6}

 

计算到V6时也一样，两条路径的消耗相同，都保留。

最终结果是只去掉了路径a：

则此时源点V1到汇点V6的路径，即原图中的关键路径有三条：

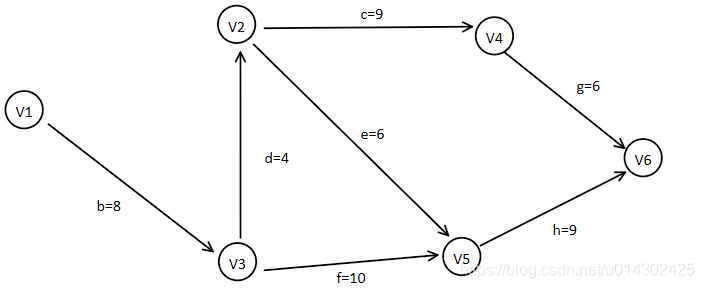
1. bfh
2. bdeh
3. bdcg