二叉树三种遍历方式的六种实现方法

一、基本概念

每个结点最多有两棵子树，左子树和右子树，次序不可以颠倒。

性质：

1、非空二叉树的第n层上至多有2^(n-1)个元素。

2、深度为h的二叉树至多有2^h-1个结点。

3、对任何一棵二叉树T，如果其终端结点数(即叶子结点数)为n0，度为2的结点数为n2，则n0 = n2 + 1。

满二叉树：所有终端都在同一层次，且非终端结点的度数为2。

在满二叉树中若其深度为h，则其所包含的结点数必为2^h-1。

完全二叉树：除了最大的层次即成为一颗满二叉树且层次最大那层所有的结点均向左靠齐，即集中在左面的位置上，不能有空位置。

对于完全二叉树，设一个结点为i则其父节点为i/2，2i为左子节点，2i+1为右子节点。

二、二叉树的遍历

遍历二叉树的所有结点且仅访问一次。按照根节点位置的不同分为前序遍历，中序遍历，后序遍历。

前序遍历：根节点->左子树->右子树（根节点在前面）

中序遍历：左子树->根节点->右子树（根节点在中间）

后序遍历：左子树->右子树->根节点（根节点在后边）

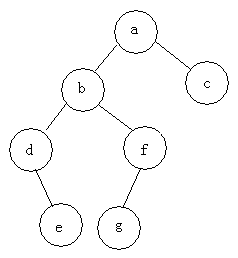
例如：求下面树的三种遍历

 

前序遍历：abdefgc

中序遍历：debgfac

后序遍历：edgfbca

三、二叉树三种遍历方式的六种实现方法

#include <iostream>
#include <string>
#include <stack>
#include <vector>
using namespace std;
struct Node
{
	int val;
	Node * left;
	Node * right;
	Node(int x) :val(x), left(nullptr), right(nullptr){};
};

void creatBiTree(Node * &root)
{
	int x;
	cin >> x;
	if (x == -1)
	{
		root = nullptr;
		return;
	}
	root = new Node(x);
	creatBiTree(root->left);
	creatBiTree(root->right);
}
void visit(Node *T)
{
	if (T->val != -1)
		cout << T->val << " ";

}
/**递归方式遍历**/
//先序递归遍历
void preOrder(Node * root)
{
	if (root != nullptr)
	{
		visit(root);
		preOrder(root->left);
		preOrder(root->right);
	}
}
//中序递归遍历
void inOrder(Node * root)
{
	if (root != nullptr)
	{
		inOrder(root->left);
		visit(root);
		inOrder(root->right);
	}
}
//后序递归遍历
void postOrder(Node * root)
{
	if (root != nullptr)
	{
		postOrder(root->left);
		postOrder(root->right);
		visit(root);
	}
}
/**非递归方式遍历**/
//先序遍历
void preOrderF(Node * root)
{
	if (root == nullptr)
		return;
	stack<Node *> s;
	s.push(root);
	Node *p = nullptr;
	while (!s.empty())
	{
		p = s.top();
		s.pop();
		cout << p->val << " ";
		if (p->right)
			s.push(p->right);
		if (p->left)
			s.push(p->left);
	}
}
//中序遍历
void inOrderF(Node * root)
{
	if (root == nullptr)
		return;
	stack<Node *> s;
	Node *p = root;
	while (p||!s.empty())
	{
		if (p)
		{
			s.push(p);
			p = p->left;
		}
		else 
		{
			p = s.top();
			s.pop();
			cout << p->val << " ";
			p = p->right;
		}
	}
	
}
//后序遍历
void postOrderF(Node * root)
{
	if (root == nullptr)
		return;
	stack<Node *> s;
	vector<int> rs;
	s.push(root);
	Node *p = nullptr;
	while (!s.empty())
	{
		p = s.top();
		s.pop();
		rs.insert(rs.begin(),p->val);
		if (p->left)
			s.push(p->left);
		if (p->right)
			s.push(p->right);
	}
	for (int i = 0; i < rs.size(); i++)
		cout << rs[i] << " ";
}
int _tmain(int argc, _TCHAR* argv[])
{
	Node * root;
	//二叉树的创建(根据先序创建)
	creatBiTree(root);
	//二叉树的递归遍历
	preOrderF(root);
	cout << endl;
	inOrderF(root);
	cout << endl;
	postOrderF(root);
	cout << endl;
	return 0;
}