各排序算法循环版本(C++)

排序也是一种基础，让我们来看看，此外这里都是默认升序排序。

冒泡排序

假设数组v大小为n，v[i]与v[i+1]比较，如果v[i]大就交换，第一趟循环结束，v[n-1]必定为最大，第二趟v[n-2]必定第二大，以此类推

void bubble_sort(std::vector<int>& v)
{
	for (size_t i = v.size(); i > 1; i--)
	{
		size_t count = 0;
		for (size_t j = 0; j < i - 1; j++)
		{
			if (v[j] > v[j + 1])
				swap(v, j, j + 1);
			else
				count++;
		}
		if (count == i - 1)    //计数器记录无交换次数，如果等于当前趟待排个数则表示已排序完成
			break;
	}
}

void swap(std::vector<int>& v, size_t src, size_t dst)
{
	int temp = v[src];
	v[src] = v[dst];
	v[dst] = temp;
}

插入排序

v[i]与v[i-1]比较，如果v[i]小，交换，然后v[i-1]与v[i-2]比较，类推，直到比前一个大结束。

void insertion_sort(std::vector<int>& v)
{
	for (size_t i = 1; i < v.size(); i++)
	{
		for (size_t j = i; j > 0 && v[j] < v[j-1]; j--)
		{
			swap(v, j, j - 1);
		}
	}
}

希尔排序

希尔排序只是改变排序对象，使用的方法还是和上面两个一样，都是朝前或朝后比较然后交换。首先，希尔排序需要一个增量序列，比如Hibbard增量序列，2^k-1。比如1-3-7-15，首先v[i]与v[i+15]比较，然后和前面一样，只不过步长不是1是15，然后第二趟循环就是v[i]与v[i+7]，以此类推。排序效率与增量序列的选择关系比较大。

void shell_sort(std::vector<int>& v)
{
	std::vector<int> hibbardVec;
	hibbardVec = hibbard(5);
	for (int i = hibbardVec.size()-1; i >= 0; i--)
		shell_sort(v, hibbardVec[i]);
}

void shell_sort(std::vector<int>& v, size_t k)
{
	if (k > v.size())
		return;
	for (size_t n = v.size() / k; n > 1; n--)
	{
		int count = 0;
		for (size_t i = 0; i < n-1; i++)
		{
			if (v[i] > v[i + k])
				swap(v, i, i + k);
			else
				count++;
		}
		if (count == n - 1)
			break;
	}
}

std::vector<int> hibbard(int k)
{
	std::vector<int> v;
	v.resize(k);
	for (size_t i = 1; i <= v.size(); i++)
		v[i-1] = (int)std::pow(2, i) - 1;
	return v;
}

堆排序

因为堆的根节点总是最大值或最小值，所以如果能把数据放在堆里面，每次取根节点依次排好就行。堆的构造可以参考大小堆的实现（C++）

void heap_sort(std::vector<int>& v)
{
	BinaryTreeNode<int> *p = InitHeap(v, MIN);
	for (size_t i = 0; i < v.size(); i++)
		v[i] = tree::DeleteHeap(p, MIN);
	delete p;
}

归并排序

这是一种自下而上的方法，首先对最小规模子集排序，也就是两两之间比较，然后向上合并

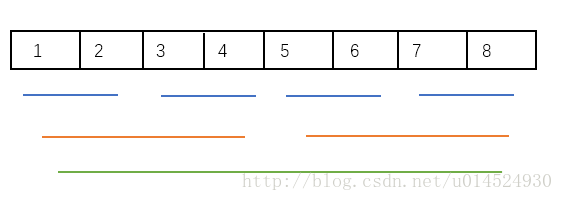
这个用递归是比较好实现的，向下递归就好。如果要使用循环实现可以使用类似前面的增量序列，我们可以发现每次循环，排序子集都是2^k大小，我们借此设置步长的增加。

void merge_sort(std::vector<int>& v)
{
	int k = 0;
	int stride = 0;
	int n = v.size();
	if (n < 2)
		throw std::exception("数组小于2无法排序");
	std::vector<int> _v;
	_v.resize(n);
	while ((stride=(int)pow(2,k)-1) < n) {
		int start = 0;
		while (start < n) {
			int ls = start;
			int le = ls + stride;
			int rs = le + 1;
			int re = rs + stride;
			if (re > n-1) {
				if (rs < n)
					merge_sort(v, ls, le, rs, n - 1, _v);
				break;
			}
			merge_sort(v, ls, le, rs, re, _v);
			start = re + 1;
		}
		k++;
	}
}

//ls为left start，le为left end
void merge_sort(std::vector<int>& v, int ls, int le, int rs, int re, std::vector<int>& _v)
{
	int start = ls;
	int begin = ls;
	int end = re;
	while ((ls <= le && rs <= re)) {
		if (v[ls] > v[rs]) {
			_v[start] = v[rs];
			rs++;
		}
		else
		{
			_v[start] = v[ls];
			ls++;
		}
		start++;
	}
	while (ls <= le) {
		_v[start] = v[ls];
		ls++;
		start++;
	}
	while (rs <= re) {
		_v[start] = v[rs];
		rs++;
		start++;
	}
	vec_copy(_v, v, begin, end);
}

//复制指定范围
void vec_copy(std::vector<int> &src, std::vector<int> &dst, int start, int end)
{
	for (int i = start; i <= end; i++)
		dst[i] = src[i];
}

这里写的复杂了点，用了4个范围参数，但是比较好理解，当然数组复制的地方使用内存地址copy会快些，但是这样比较好调试。

快速排序

为什么叫快速排序，因为它在一般情况下，也就是不会拿一个已经排序的数据再去走一遍，这种时候快速排序是比较蠢的，还得走一遍。一般情况下，它的时间复杂度上界是比较低而且稳定的，可以达到NlogN的等级。和上面的有点类似，但快速排序是一种自上而下的方法。它首先选定一个元素，然后找出比它小的全部放一起，比它大的全部放一起，然后递归处理子集，最后当子集大小为2时，也就全部有序了。但是这个元素选取也比较重要，从半分查找我们可以看出，如果想要效率最快，我们必须靠近中点。常见的是选取首中尾三个元素的中值作为锚点。

首先我们定义一个结构用于保存数组子集范围

	struct Range
	{
		int begin;
		int end;
		Range(int b,int e) {
			begin = b;
			end = e;
		}
	};

然后使用队列保存子集，循环处理

void quick_sort(std::vector<int>& v)
{
	std::queue<Range> q;
	Range r(0, v.size() - 1);
	q.push(r);
	while (!q.empty()) {
		Range _r = q.front();
		q.pop();
		int mid = quick_sort(v, _r.begin, _r.end);
		if (mid != -1) {
			Range lr(_r.begin, mid-1);
			Range rr(mid+1, _r.end);
			q.push(lr);
			q.push(rr);
		}
	}
}

int quick_sort(std::vector<int>& v, int begin, int end)
{
	int flag = end - begin;
	if (flag < 2) {
		if (v[begin] > v[end])
			swap(v, begin, end);
		return -1;
	}
	int pvt = pivot(v, begin, end);
	int smaller = begin;
	int bigger = end - 2;
	while (true) {
		while ((v[smaller] <= v[pvt]) && (smaller!=pvt))
			smaller++;
		while (v[bigger] >= v[pvt])
			bigger--;
		if (smaller > bigger)
			break;
		swap(v, smaller, bigger);
	}
	swap(v, pvt, smaller);
	return smaller;
}

int pivot(std::vector<int>& v, int begin, int end)
{
	int mid = (begin + end) / 2;
	if (v[begin] > v[mid]) 
		swap(v, begin, mid);
	if (v[begin] > v[end]) 
		swap(v, begin, end);
	if (v[mid] > v[end]) 
		swap(v, mid, end);
	swap(v, mid, end - 1);    //把中值存放在倒数第二位置，便于后面排序
	return end - 1;
}

至于表排序与基数排序，这两者更多的是应用的方式，而不是算法，这里就不讨论了。