我们来看一下插值查找。
本页内容
1.插值查找原理
2.代码实现
3.总结评价
1.插值查找原理
插值查找的前提是有序数列元素的值是成线性增长的。对于大多数有序数列来说,这前提是可以成立的。我们不妨假设它就是成立的,那样,当我们知道一个要查找值的大小后。就可以根据数列线性增长的性质,求出要查找的值在数列中的大概位置。比如说在数列A[lo,hi)中查找e。我们设e的下标为mi。由于数列线性增长,我们不难得到这个等式:
进而得出:
我们可求出mi的值,以它为轴点,可以极大的提高查找的收敛速度。说到这里,大家也都明白了,其实插值查找就是更准的二分查找而已。
2.代码实现
#include<iostream>
using namespace std;
int InterpolationSearch(int *A,int e,int lo,int hi)
{
while(lo<hi)
{
int mi=lo+(hi-lo-1)*(e-A[lo])/(A[hi-1]-A[lo]);//获取查找轴点
if(mi>=10)//排除越界情况
{
return -1;
}
if(e<A[mi])
{
hi=mi;//深入左侧[lo,hi)
}
else if(e>A[mi])
{
lo=mi+1;//深入右侧[mi+1,hi)
}
else
{
return mi;//命中
}
}
return -1;//查找失败
}
int main()
{
/*******插值查找测试******/
int a[10];
cout<<"测试数组:";
for(int i=0;i<10;i++)
{
a[i]=(float)(i);
cout<<a[i]<<" ";
}
cout<<endl;
cout<<"查找结果:" ;
for(int i=0;i<13;i++)
{
cout<<InterpolationSearch(a,i-1,0,10)<<" ";
}
cout<<endl;
/***************************/
}
3.总体评价
插值查找比二分查找有所改进,但是其效率提高的并不明显(除非所查找的数列特别庞大,它的用处才能显现)。算法中引用了乘法和除法,增加了额外的消耗。如果所需查找的数列不大,由于每次深入都要进行乘除操作,用此算法可能得不偿失。所以,在实际应用中,该算法常常与二分查找算法联合使用,来处理较大的数据:用插值查找将数据缩小到一定范围,再用二分查找完成查询。












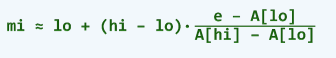















 124
124

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








