一、欧拉函数
思考:任意给定正整数n,请问在小于等于n的正整数之中,有多少个与n构成互质关系?
解:计算这个值的方法就叫做欧拉函数,以φ(n)表示。
怎样求一个任意数的欧拉函数值?
其中(3)为欧拉函数的通用计算形式。
实现代码:
long phi(long n)
{
long ans=n;
for (long i=2; i*i<=n; i++) //寻找素数pi(任意一个正整数可以分解成唯一的质因数的乘积,所以从小到大的找,则符合条件的一定是素数)
{
if(n%i==0) //n能被i整除
{
n/=i;
ans=ans-ans/i;//ans=ans*(1-1/i)
while (n%i==0) //找出素数pi对应的指数是多少
{
n/=i;
}
}
}
if(n>1)
{
ans=ans-ans/n;
}
return ans;
}可以用 poj2407来测试代码。
二、费马定理
如果p是素数并且a是不能被p整除的正整数,那么:
费马定理的另一种形式:
如果p是素数,a是任意正整数,则对gcd(a,p)=1,有:
证明:
因为p是素数,所以a、p互素,所以集合{a,2a,3a,…,(p-1)a}在同余意义下等价于{1,2,3,…,(p-1)}(注:元素顺序可能不同)
所以a×2a×3a×…×(p-1)a≡1×2×3×…×(p-1) mod p,即(p-1)!a^(p-1)≡(p-1)!mod p,所以a^(p-1)≡1mod p,也即ap≡a mod p。
来看道例题:
三、欧拉定理
若整数a与整数n互素,则:
如果n=p是素数,则有
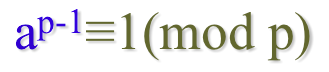
显然,欧拉定理可以看成是费马定理的推广形式。
下面来看看一道例题:











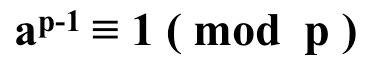
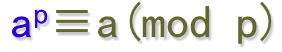

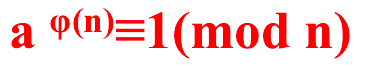



















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








