CVPR2016
https://github.com/KaimingHe/deep-residual-networks
这是微软方面的最新研究成果, 在第六届ImageNet年度图像识别测试中,微软研究院的计算机图像识别系统在几个类别的测试中获得第一名。
本文是解决超深度CNN网络训练问题,152层及尝试了1000层。
随着CNN网络的发展,尤其的VGG网络的提出,大家发现网络的层数是一个关键因素,貌似越深的网络效果越好。但是随着网络层数的增加,问题也随之而来。
首先一个问题是 vanishing/exploding gradients,即梯度的消失或发散。这就导致训练难以收敛。但是随着 normalized initialization [23, 9, 37, 13] and intermediate normalization layers[16]的提出,解决了这个问题。
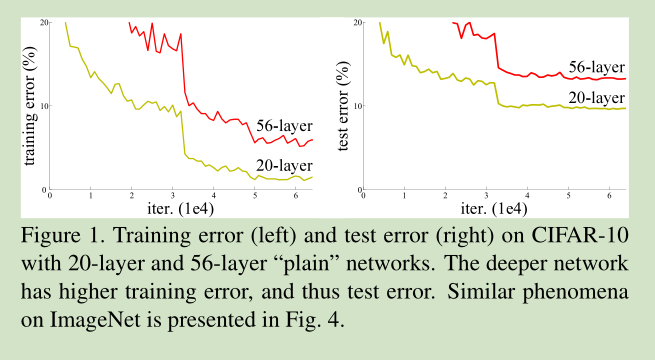
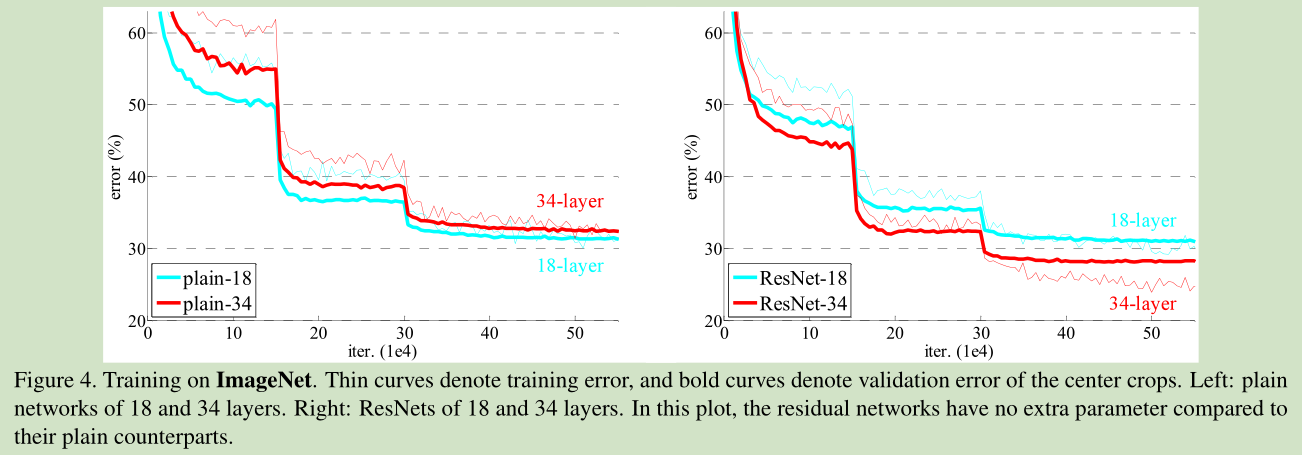
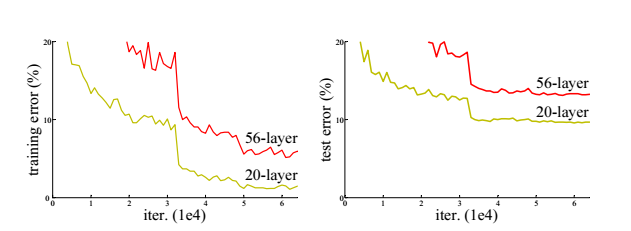
当收敛问题解决后,又一个问题暴露出来:随着网络深度的增加,系统精度得到饱和之后,迅速的下滑。让人意外的是这个性能下降不是过拟合导致的。如文献 [11, 42]指出,对一个合适深度的模型加入额外的层数导致训练误差变大。如下图所示:
如果我们加入额外的 层只是一个 identity mapping,那么随着深度的增加,训练误差并没有随之增加。所以我们认为可能存在另一种构建方法,随着深度的增加,训练误差不会增加,只是我们没有找到该方法而已。
这里我们提出一个 deep residual learning 框架来解决这种因为深度增加而导致性能下降问题。 假设我们期望的网络层关系映射为 H(x), 我们让 the stacked nonlinear layers 拟合另一个映射, F(x):= H(x)-x , 那么原先的映射就是 F(x)+x。 这里我们假设优化残差映射F(x) 比优化原来的映射 H(x)容易。
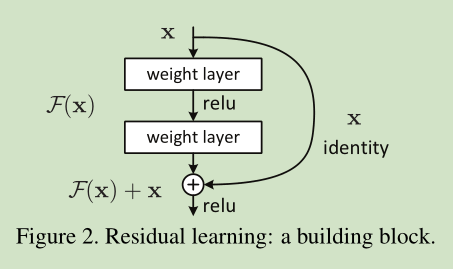
F(x)+x 可以通过shortcut connections 来实现,如下图所示:
2 Related Work
Residual Representations
以前关于残差表示的文献表明,问题的重新表示或预处理会简化问题的优化。 These methods suggest that a good reformulation or preconditioning can simplify the optimization
Shortcut Connections
CNN网络以前对shortcut connections 也有所应用。
3 Deep Residual Learning
3.1. Residual Learning
这里我们首先求取残差映射 F(x):= H(x)-x,那么原先的映射就是 F(x)+x。尽管这两个映射应该都可以近似理论真值映射 the desired functions (as hypothesized),但是它俩的学习难度是不一样的。
这种改写启发于 图1中性能退化问题违反直觉的现象。正如前言所说,如果增加的层数可以构建为一个 identity mappings,那么增加层数后的网络训练误差应该不会增加,与没增加之前相比较。性能退化问题暗示多个非线性网络层用于近似identity mappings 可能有困难。使用残差学习改写问题之后,如果identity mappings 是最优的,那么优化问题变得很简单,直接将多层非线性网络参数趋0。
实际中,identity mappings 不太可能是最优的,但是上述改写问题可能对问题提供有效的预先处理 (provide reasonable preconditioning)。如果最优函数接近identity mappings,那么优化将会变得容易些。 实验证明该思路是对的。
3.2. Identity Mapping by Shortcuts
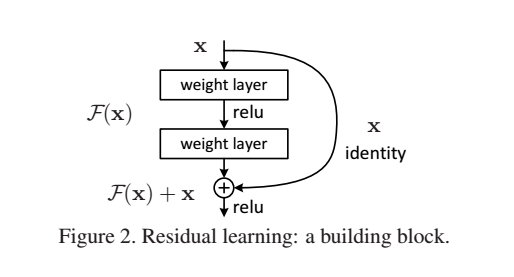
图2为一个模块。A building block
公式定义如下:
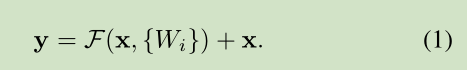
这里假定输入输出维数一致,如果不一样,可以通过 linear projection 转成一样的。
3.3. Network Architectures
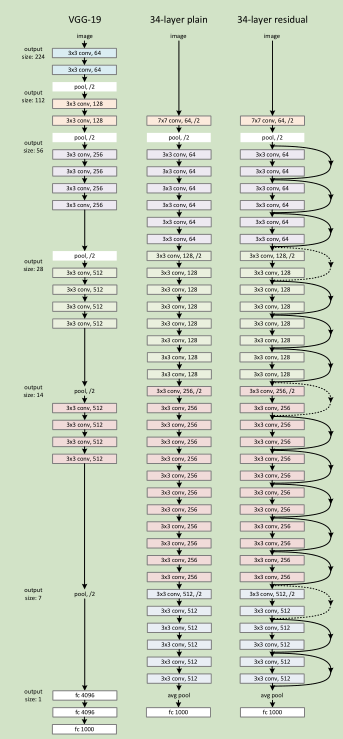
Plain Network 主要是受 VGG 网络启发,主要采用3*3滤波器,遵循两个设计原则:1)对于相同输出特征图尺寸,卷积层有相同个数的滤波器,2)如果特征图尺寸缩小一半,滤波器个数加倍以保持每个层的计算复杂度。通过步长为2的卷积来进行降采样。一共34个权重层。
需要指出,我们这个网络与VGG相比,滤波器要少,复杂度要小。
Residual Network 主要是在 上述的 plain network上加入 shortcut connections
3.4. Implementation
针对 ImageNet网络的实现,我们遵循【21,41】的实践,图像以较小的边缩放至[256,480],这样便于 scale augmentation,然后从中随机裁出 224*224,采用【21,16】文献的方法。
4 Experiments
论文下载:
Deep Residual Learning for Image Recognition
CVPR2016最佳论文,夺得ImageNet recognition, ImageNet detection, ImageNet localization, COCO detection, and COCO segmentation五项第一。
这篇论文由微软研究院的四人团队:Kaiming He、Xiangyu Zhang、Shaoqing Ren、Jian Sun发表,解决了深层网络训练和测试误差低的问题。
摘要
提出了一种残差学习方式,让训练比以往更深的网络更为简单。在大量的实验仿真基础上,证实了这种残差网络确实更易于优化并且通过增加层数获得更准确的结果。这种方法可用于图像识别的各个方面(image classification,object detection等等)
但是这里我觉得这种方法还可以用于其他地方,比如训练一个全连接的网络,不一定是CNN,普通的网络应该也能提升效果
介绍
深度卷积网络已经取得了一系列的成就,因为他能很好的结合图像底层到高层语义上的各个特征。最新的研究表明网络深度还是一个至关重要的因素,在ImageNet数据集上,领先的几个模型都使用了很深的模型(16-30层不等),其他数据集上同样也是,深层模型会有更好的表现。
但是深层模型同样带来了问题:第一就是著名的梯度弥散和爆炸问题,导致结果不会收敛。但是这个问题通过normalized initialization和intermediate normalization layers可以解决(我在后面的博客中会解释讨论这个问题)。同时,作者还发现了一个问题,深层网络会导致“精度下降”,但是这种“精度下降”并不是过拟合导致的(下图显示了作者的结果)
于是就产生了这样一个问题:假设我们训练了一个浅层网络,它的error已经稳定,然后我们在它的基础上又添加了多个层,但是error增加了。
作者考虑到了某一种特殊情况,假设添加进去的多个层不改变原先的输出,相当于做一个恒等映射(实际上这就是当前网络的一个solution),那么这
一个solution应该与原网络的error一样,而实际中却并不能找到这样的solution。
作者在论文中提出了一个深度残差学习框架来解决这个“精度下降”问题,即不通过堆叠一些层直接学习从input到output的映射,而是让他们学习一个残差映射,具体结构图如下:F(x)是在x基础上的残差,如果用H(x)表示目标映射的话,那么F(x)=H(x)-x。在这个前提下,我们知道最后的目标输出就是F(x)+x,x这个量通过输入端的一个shortcut connection连接到输出,这种形式就构成了短路结构。这一个短路连接,实现的是x的恒等映射,而且它并没有带入任何参数,也没有增加任何的计算复杂性。
相关工作
残差表示的思想在之前就比较广泛了,作者列举了一些前人使用残差表示的例子:VLAD和Fisher Vector都是有效的图像分类方法,偏微分方程的数值解法多重网格法,就是把问题分为在不同尺度上的子问题,然后通过求解粗尺度和细尺度上的差分量来估计方程的解。(多重网格法很有意思,有兴趣的同学可以研究一下,它很好的贯彻了残差和迭代的思想)。而且往往求解残差会比求解原解收敛得更快。
短路连接的思想来源于早期训练多层感知机时会添加一个从input到output的线性层来进行优化。当然,早期也使用在中间层添加一个额外的分类器来解决梯度弥散爆炸问题。作者还提到了“高速公路网络”,它用门限函数来作为短路连接的映射,与之对比,本文的网络实现恒等映射而且不需要额外的参数,当断开时,shortcut就不起作用了,原先的映射就不再是残差映射而退化成input到output的映射,反观自己的网络,连接永远不会断开。在深层结构下,“高速公路网络”的精确度并不会提升。(这里就是对“高速公路网络”的思想一顿批……)
实现
这一部分作者再次讨论了残差学习的实现细节。之所以选择学习一个残差,是因为残差有时候会比原映射更容易学习,设想一个特殊的情况:
如果我们的目标映射就是恒等映射,那么残差学习的结果就会简单地把所有的权值置为0,以获得恒等映射。然而在原来的网络,这个步骤将会很复杂,恒等映射通过多个非线性层去学习,不仅耗费计算,而且必然会产生误差。作者认为,深层网络之所以会产生精度下降问题,就是这些误差累加所导致的。
在现实中,显然恒等映射不会是目标映射了,但是短路结构为后续的学习提供了一个先验信息,我们只需要处理这个信息上的扰动,而不用重新学习一个新的映射,这就是本文思想的核心所在。
短路连接还需要解决一个问题就是input和output维度不同的问题,F(x)和x的维度不同,就意味着x需要升维或者降维
假设W是一个线性变换矩阵
使用y=F(x)+Wx来进行维度的匹配
那么W到底怎么确定呢?文中没有给出一个明确的解答,这也是我阅读这篇论文的最大疑问。
最后展示一下论文中的34-layer residual大致结构,与普通的CNN34-layer plain和VGG-19的对比。
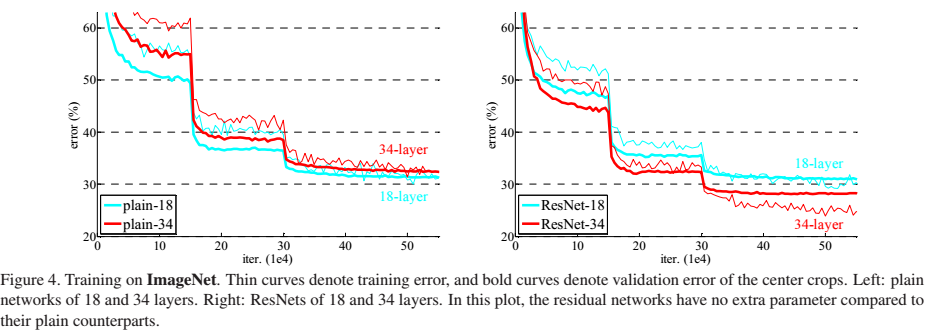
普通网络和ResNet的error对比
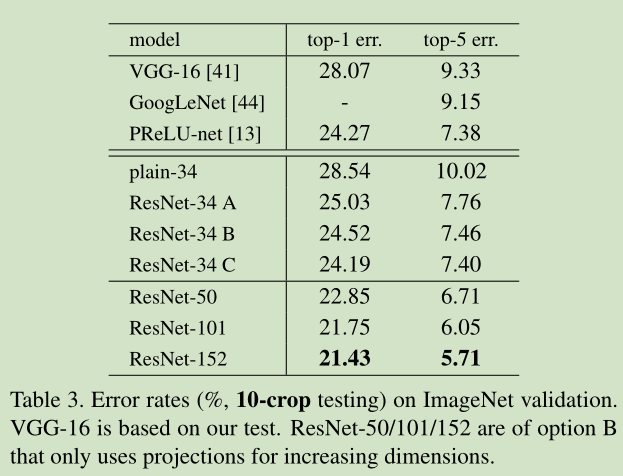
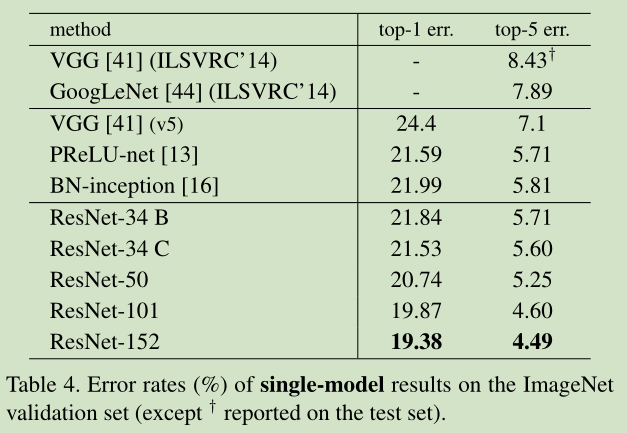
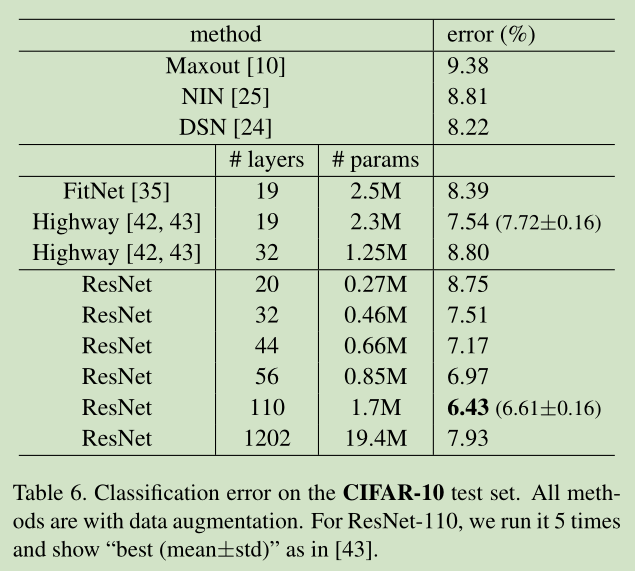
这个误差表证明了论文的观点,确实ResNet可以随着深度的增加而变得精确,看到152层网络有点害怕,训练一个这么大的网络,需要调度多少的高性能GPU。。。这年头搞科研也要用钱砸啊
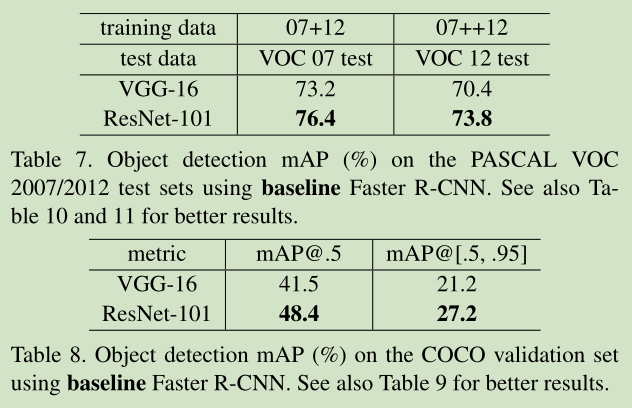
ResNet-A、B、C代表了0填充升维、projection升维,其他的用恒等映射、全部用projection三种方法,C的准确度最高,不过文章也说了,W不管怎么取值,都可以解决“精度下降”的问题,所以W并不是关键点。
























 2905
2905

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








