高速旋转的磁悬浮轴承系统中,一个微米级的质量偏心足以引发灾难性振动。如何驯服这只“旋转的猛兽”?核心在于精准的不平衡控制策略。
引言:高速旋转世界的“阿喀琉斯之踵”
磁悬浮轴承(Active Magnetic Bearing, AMB)凭借无接触、无摩擦、高速度、长寿命等革命性优势,已成为高端旋转机械(如高速电机、离心压缩机、飞轮储能)的核心支撑技术。然而,转子固有的不平衡质量分布始终是悬在其头上的“达摩克利斯之剑”。当转子高速旋转时,不平衡质量产生的周期性离心力会激励转子产生同步振动。若控制不当,轻则导致精度下降、噪声增大,重则引发系统失稳、转子碰磨甚至设备损毁。因此,实现转子不平衡质量的有效抑制,是磁悬浮轴承走向工程化、实用化的必经之路。
一、磁悬浮轴承与不平衡振动的核心原理
-
AMB 工作原理简述:
-
AMB 利用电磁力实现转子的无接触悬浮。
-
通过位置传感器实时监测转子位移。
-
控制器根据位移偏差信号,结合控制算法(如 PID、H∞、自适应等)计算出所需的控制电流。
-
功率放大器将控制电流信号放大,驱动电磁铁产生精确的电磁力,将转子稳定悬浮在设定位置(通常是几何中心)。
-
-
不平衡振动的产生机制:
-
转子的质量中心(CM)与其几何中心(旋转中心,RC)存在微小偏移
e(即偏心距)。 -
当转子以角速度
ω旋转时,偏心质量m_u产生周期性离心力:F_u = m_u * e * ω²。 -
该力作用于转子上,方向随旋转不断变化,试图将转子拉向其质量中心旋转的轨迹(即不平衡响应)。
-
AMB 系统必须产生一个与之抗衡的电磁力
F_c,以维持转子围绕几何中心旋转。
-
二、不平衡控制的深层挑战与核心目标
-
核心挑战:
-
陀螺效应: 高速旋转时,陀螺力矩使转子的径向振动在两个正交方向上耦合,增加了控制复杂性。
-
传感器干扰: 位移传感器输出中不仅包含几何中心位移,还混杂着由于转子弯曲、传感器安装误差等引起的同频振动信号(runout),干扰控制器对真实不平衡位移的判断。
-
模型不确定性: 转子的不平衡量大小和相位通常是未知且可能缓慢变化的(如热变形、磨损)。
-
控制器带宽限制: AMB 系统存在固有动态特性(电磁铁电感、功率放大器带宽、机械结构模态),控制器无法无限提升增益来抑制所有频率的振动。
-
负刚度特性: 磁悬浮轴承本身具有被动负刚度特性,需要控制器提供额外的正刚度来维持稳定。
-
-
控制目标:
-
稳定性: 首要目标是确保转子在整个工作转速范围内(尤其是穿越临界转速时)稳定悬浮。
-
振动抑制: 有效抑制由不平衡质量引起的同步振动(1X 频率分量),最小化转子绕几何中心的位移峰峰值。
-
传递力抑制: 降低不平衡力通过磁轴承传递到基座的力,减少整机振动和噪声。
-
鲁棒性: 控制策略应对不平衡量变化、模型参数摄动等具有适应性或鲁棒性。
-
三、核心控制策略:从基础到进阶
不平衡控制策略需在保证系统整体稳定性的前提下,针对性地处理同步振动分量。以下策略常结合使用:
-
基础层:PID 控制与刚度阻尼补偿
-
作用: 提供基础悬浮稳定性和动态响应。PID 控制器是 AMB 系统的核心闭环控制器。
-
设计要点:
-
稳定性设计: 基于转子动力学模型(考虑刚体模态和可能的柔性模态)进行频域分析(Bode, Nyquist)或时域分析(极点配置),整定 PID 参数(
Kp,Ki,Kd),确保系统在零速和低速时稳定,并具有足够的幅值裕度和相位裕度穿越临界转速。 -
负刚度补偿: 控制器需提供足够的正刚度
K_c以抵消磁轴承固有的负刚度K_m(K_c > |K_m|)。 -
阻尼注入: 提供足够的正阻尼
C_c以抑制振荡,提高稳定性裕度。
-
-
局限性: 单一 PID 在抑制特定频率(尤其是同步频率)的振动时效率不高,高增益虽能抑制振动但会降低鲁棒性并放大噪声。
-
-
核心武器:陷波滤波器
-
作用: 选择性衰减特定频率(即转速频率
ω)附近的信号分量,是抑制同步振动的最常用且有效的手段。 -
原理: 在反馈回路或前馈通道中串联一个传递函数,使其在目标频率
f_n = ω/(2π)处具有深度的衰减(陷波),而对其他频率影响较小。 -
标准形式:
G_notch(s) = (s² + 2ζ1ω_n s + ω_n²) / (s² + 2ζ2ω_n s + ω_n²)
-
ω_n = 2πf_n:陷波中心频率(rad/s)。 -
ζ1:控制陷波深度(ζ1越小,陷波越深)。 -
ζ2:控制陷波宽度(ζ2越大,陷波越宽)。
-
-
设计步骤:
-
频率锁定: 实时获取转子转速
ω(通常由驱动系统或编码器提供),计算f_n = ω/(2π)。 -
参数整定:
-
深度 (
ζ1): 根据所需振动衰减程度选择。过深可能导致该频率附近相位突变过大,危及稳定性(需结合稳定性分析)。典型值范围0.01 ~ 0.1。 -
宽度 (
ζ2): 考虑转速波动范围。转速波动大时需较宽陷波(ζ2较大,如0.5 ~ 1.0),以保证覆盖实际转速范围;转速稳定时可选择较窄陷波(ζ2较小,如0.1 ~ 0.3),提高选择性。
-
-
稳定性校验: 将陷波滤波器加入闭环系统模型,重新分析开环传递函数的 Bode 图或 Nyquist 图,确保在陷波频率附近及整个工作频带内幅值裕度和相位裕度仍满足要求(如 PM > 30°, GM > 6dB)。特别注意陷波引入的相位滞后对稳定性的影响。
-
实现方式: 离散化后(如双线性变换)在 DSP/FPGA 控制器中实时计算。
-
-
-
高阶策略:自适应前馈/反馈控制
-
作用: 针对未知或缓慢变化的不平衡量,自动调整控制参数,实现更优的振动抑制效果。
-
原理:
-
LMS 自适应前馈: 利用转速信号
ω作为参考输入,通过自适应算法(如最小均方 LMS)调整一组系数(通常为正余弦分量权重),生成一个与不平衡力反相的控制电流信号I_ff,直接抵消不平衡力。I_ff = A * cos(ωt) + B * sin(ωt)。 -
自适应陷波器: 陷波器的中心频率
ω_n自动跟踪转速ω,同时根据振动反馈信号(如 1X 频率分量幅值)自适应调整陷波深度ζ1甚至宽度ζ2,以达到最优抑制效果。
-
-
优势: 能主动适应不平衡量变化,在变转速或不平衡量变化时保持良好性能。
-
挑战: 算法复杂度较高,需要设计自适应率以保证收敛性和稳定性。
-
-
关键技巧:相位补偿
-
问题: 系统(传感器、功放、电磁铁、控制器本身)存在固有相位滞后。当控制器发出抵消力指令时,实际的抵消力可能无法精确对准不平衡力的方向(相差 180°),导致抑制效果不佳甚至放大振动。
-
解决方案: 在陷波器或前馈通道中加入相位超前补偿。通过分析或实验测量系统在同步频率处的开环相位滞后
φ_lag,设计补偿器(如超前环节(s + a)/(s + b), a < b)使其在ω处提供约(180° - φ_lag)的相位超前,确保抵消力精确反相。
-
四、稳定控制系统设计步骤
-
系统建模:
-
建立包含转子(刚体/柔性)、电磁铁、功率放大器、传感器、控制器在内的完整动力学模型(状态空间或传递函数形式)。明确刚体模态、柔性模态频率、负刚度值、系统延迟等关键参数。
-
-
基础闭环设计:
-
设计核心 PID 控制器。通过频域分析(环路整形)或时域方法(LQR)确保系统在零速和低速下稳定,具有足够的稳定裕度,能安全穿越临界转速。验证其抑制非同步振动的能力。
-
-
不平衡抑制策略选择与设计:
-
陷波滤波器设计: 根据转速范围、波动情况,确定
ζ1,ζ2初始值。进行详细的稳定性分析,确保加入陷波后系统在全转速范围内稳定。设计相位补偿器。 -
自适应策略设计: 选择 LMS 或自适应陷波算法,设计自适应率(步长、遗忘因子等)。
-
-
仿真验证:
-
在 MATLAB/Simulink 等环境中搭建非线性仿真模型(包含限幅、饱和等实际约束)。
-
设置不同大小、相位的不平衡量。
-
在恒定转速和变速过程(特别是过临界转速)下,仿真验证:
-
基础闭环稳定性。
-
加入陷波器后同步振动的抑制效果(位移峰峰值)。
-
自适应策略对不平衡量变化的跟踪能力。
-
系统的鲁棒性(参数摄动)。
-
传递到基座的力。
-
-
-
实验调试与优化:
-
将控制算法部署到实时控制器(DSP, FPGA)。
-
低速调试: 确保基础悬浮稳定。
-
升速测试: 逐步提高转速,实时监测振动位移(尤其是 1X 分量)、控制电流、稳定性。
-
参数微调: 根据实验响应(振动幅值、相位、系统噪声水平、稳定裕度),精细调整 PID 参数、陷波深度/宽度/相位补偿量、自适应步长等。
-
变工况测试: 验证在不同转速、不同不平衡量(可加试重)下的控制效果。
-
五、效果与价值
成功实施不平衡控制策略后,磁悬浮轴承系统将展现出显著优势:
-
超低振动: 转子同步振动位移峰峰值可降低数十倍甚至百倍,达到微米乃至亚微米级。
-
平稳过临界: 即使存在较大不平衡,也能安全、平稳地穿越转子临界转速。
-
极低噪声: 显著降低由不平衡引起的电磁噪声和机械噪声。
-
延长寿命: 减少振动对轴承、转子、支撑结构的疲劳损伤。
-
提升精度: 为高精度加工、测量等应用提供稳定的旋转基准。
-
拓展应用: 使磁悬浮技术能应用于更高转速、更大功率、更严苛环境的领域。
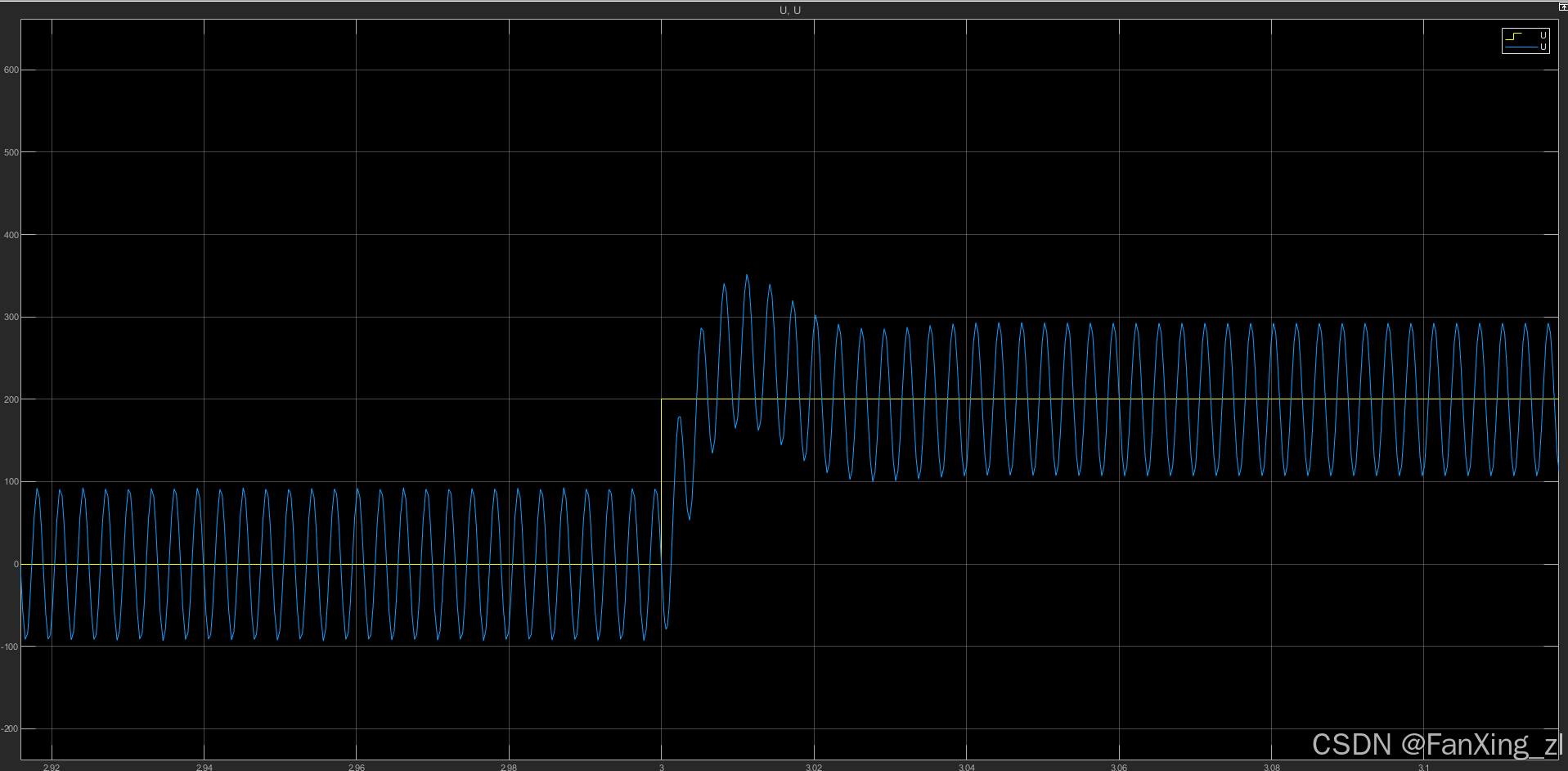
图 1: 仅基础 PID 控制下的转子位移响应(过临界转速时振动巨大)
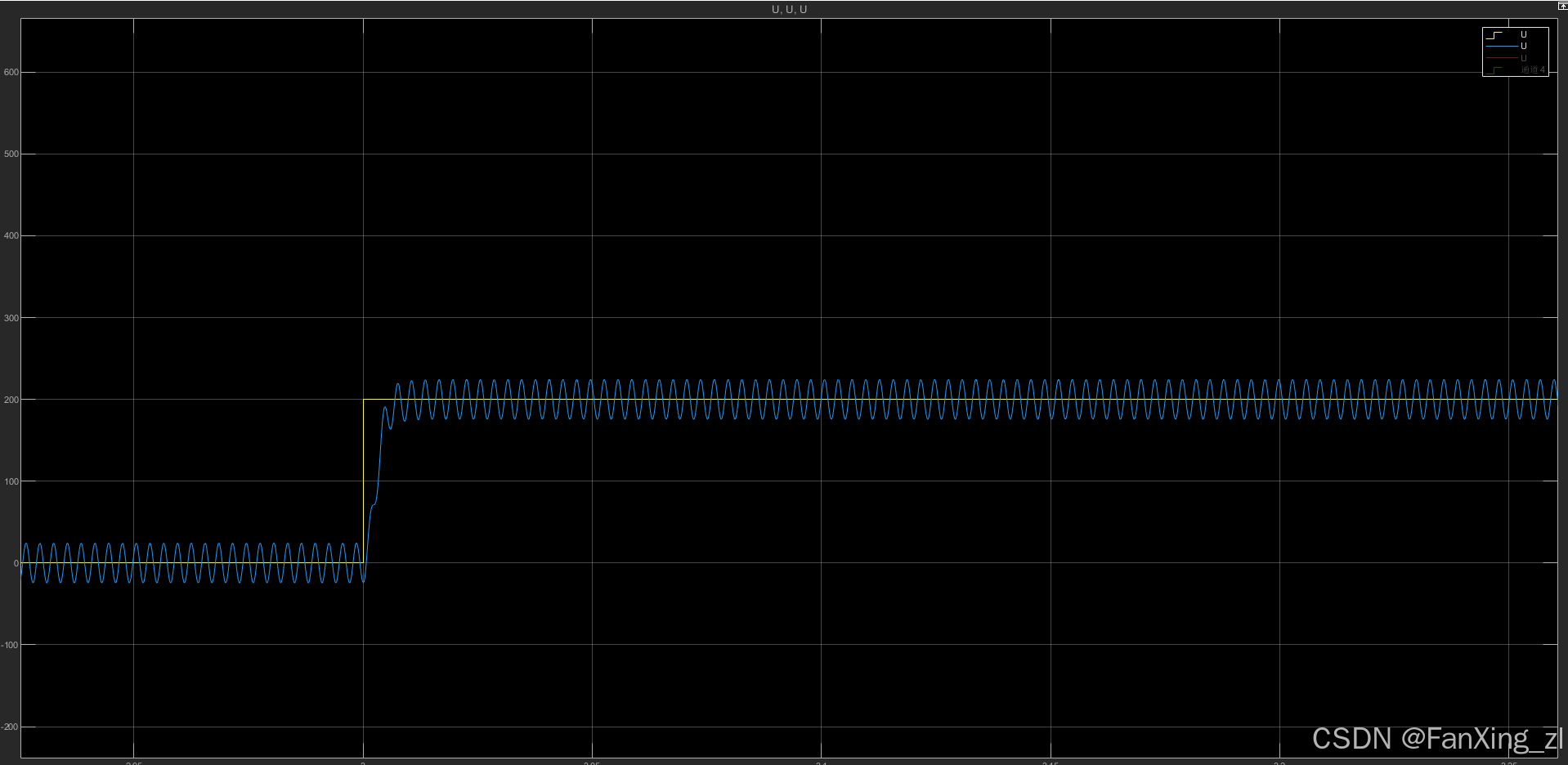
图 2: 加入优化陷波器+相位补偿后的转子位移响应(振动得到显著抑制)
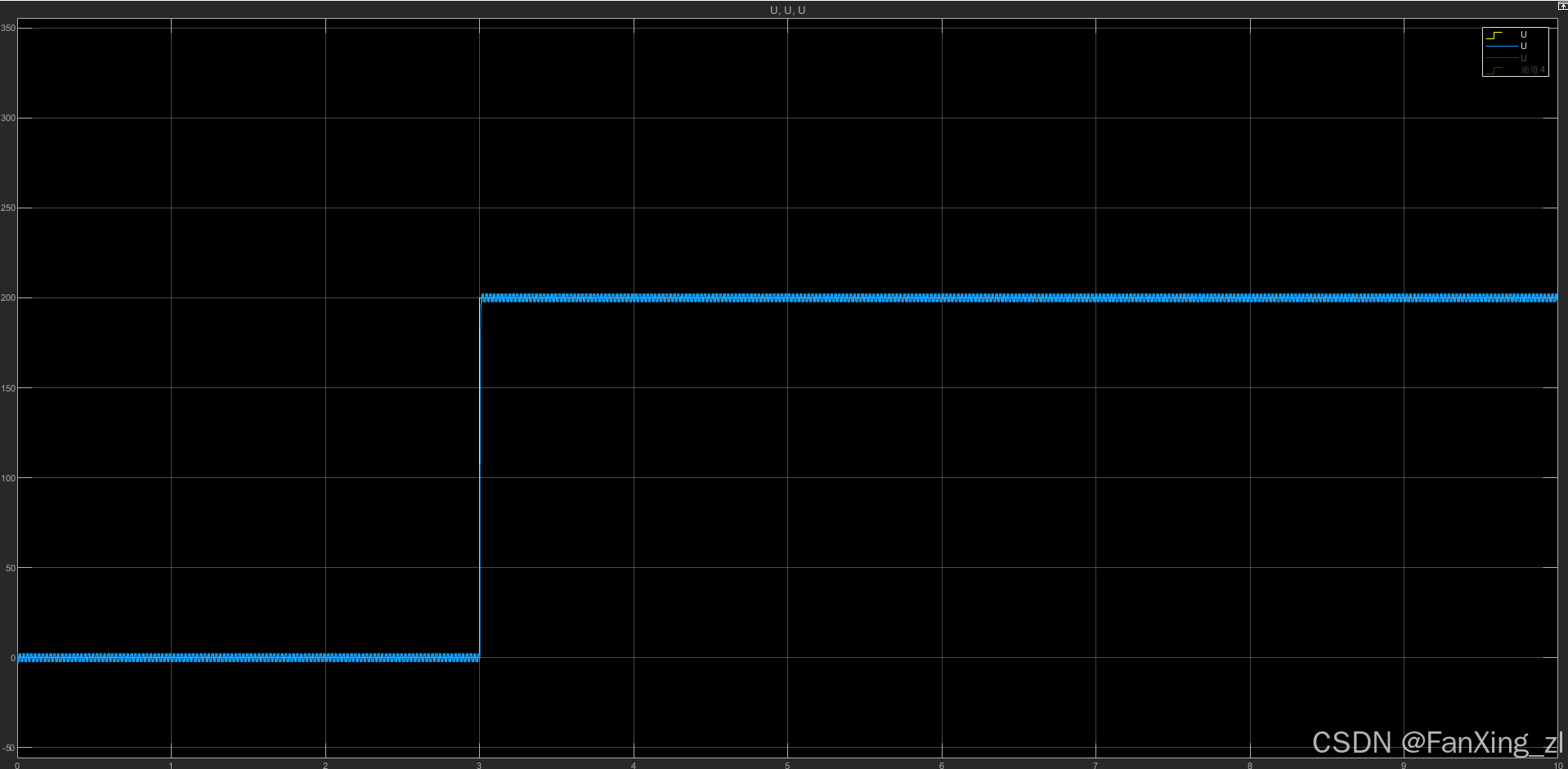
图 3: 自适应前馈控制在不同不平衡量下的抑制效果(自适应调整后均能达到低振动)
结语
磁悬浮轴承转子不平衡质量的控制,是融合了经典控制理论、信号处理、自适应算法和转子动力学的精密工程。其物理本质(不平衡力与电磁力对抗),核心工具(陷波滤波、相位补偿),并遵循严谨的建模-设计-仿真-实验流程,是解决高速旋转转子、释放磁悬浮技术全部潜力的关键。随着自适应控制、智能算法(如模糊、神经网络)的深入应用,不平衡抑制的精度、速度和鲁棒性将不断提升,为磁悬浮技术开辟更广阔的天地。





























 833
833

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










