【机器学习】集成学习：随机森林与GBDT

集成算法、随机森林、提升算法、GBDT（迭代决策树）、Adaboost（自适应增强算法）
集成学习的关键是保证弱学习器的多样性和差异性。

集成学习(Ensemble Learning)

注：集成学习相关的包均在 sklearn.ensemble下

• 集成学习是一种机器学习技术，它通过将多个学习器（分类器&回归器）进行组合产生一个新学习器来提高预测的准确性和稳定性。集成学习可以分为两种类型：平均方法和元学习方法。

平均方法中，多个学习器的预测结果被平均或投票来得出最终的预测结果。常见的平均方法包括 Bagging 和随机森林。Bagging 通过对数据集进行自助采样，生成多个独立的训练集，并在每个训练集上训练一个学习器，最终通过平均或投票来得出预测结果。随机森林是一种基于决策树的 Bagging 方法，它通过随机选择特征来增加决策树的多样性，进一步提高了模型的泛化能力。
元学习方法中，多个学习器的预测结果被输入到另一个学习器中，用来得出最终的预测结果。常见的元学习方法包括 Boosting 和 Stacking。Boosting 是一种迭代的方法，它通过提高被错误分类的样本的权重来训练多个弱学习器（weak learner），并将它们组合成一个强学习器。Stacking 是一种将多个学习器组合成一个元学习器的方法，它通过将多个学习器的预测结果作为输入，再将这些结果送入另一个学习器进行训练，最终得出最终的预测结果。

• 集成算法的成功在于保证弱分类器的多样性(Diversity)。而且集成不稳定的算法也能够得到一个比较明显的性能提升。

弱分类器(weak learner)指那些分类准确率只稍微好于随机猜测的分类器(error rate < 0.5)；

• 常见的集成学习思想有：
  • 平均方法：Bagging、随机森林
  • 元学习法：Boosting、Stacking

Why need Ensemble Learning?

1. 弱分类器间存在一定的差异性，这会导致分类的边界不同，也就是说可能存在错误。那么将多个弱分类器合并后，就可以得到更加合理的边界，减少整体的错误率，实现更好的效果；
2. 对于数据集过大或者过小，可以分别进行划分和有放回的操作（bootstrap）产生不同的数据子集，然后使用数据子集训练不同的分类器，最终再合并成为一个大的分类器（解决过拟合和欠拟合）；
3. 如果数据的划分边界过于复杂，使用线性模型很难描述情况，那么可以训练多个模型，然后再进行模型的融合；
4. 对于多个异构的特征集，可以考虑使用多个分类模型来分别处理每个特征集，然后将它们的预测结果进行融合。这种方法被称为特征级联（Feature-level Fusion）或多模态学习（Multimodal Learning）。

平均方法

Bagging方法

• Bagging方法又叫做自举汇聚法(Bootstrap Aggregating)，思想是：在原始数据集上通过有放回的抽样的方式，重新选择出S个新数据集来分别训练S个分类器的集成技术。
• Bagging方法训练出来的模型在预测新样本分类/回归的时候，会使用多数投票或者求均值的方式来统计最终的分类/回归结果。
• Bagging方法的关键在于训练集的随机采样和子模型的多样性，这可以有效减少模型的方差并提高模型的泛化能力。
• Bagging方法的弱学习器可以是基本的算法模型，eg: Linear、Ridge、Lasso、Logistic、Softmax、ID3、C4.5、CART、SVM、KNN等。
• NOTE：Bagging方式是有放回的抽样，并且每个子集的样本数量必须和原始样本数量一致，所以抽取出来的子集中是存在重复数据的，模型训练的时候允许存在重复数据。
• NOTE：差不多有1/3的样本数据是不在Bagging的每个子模型的训练数据中的。
$\underset{x\to \infty }{\lim }(1-\frac{1}{m}{)}^m=\frac{1}{e}\approx 0.368$

Bagging方法_训练过程

下面是使用Bagging方法进行训练的步骤：

1. 准备训练集：从原始数据中随机有放回地抽取一定数量的样本，作为新的训练集。这个过程可以进行多次，每次抽取的训练集都可能不同。
2. 构建子模型：使用训练集进行模型训练，得到一个子模型。这个过程可以进行多次，每次训练使用的训练集和模型都可能不同。
3. 集成子模型：将多个子模型的预测结果进行平均或投票等方式进行集成，以得到最终的模型预测结果。
4. 评估模型：使用测试集对模型进行评估，统计模型的预测准确率、精度、召回率等指标。
5. 调整模型：根据评估结果对模型进行调整，例如增加或减少子模型数量、改变子模型的参数设置等。

重复2~5步骤，直到得到满意的模型为止。

Bagging方法_预测过程

Bagging方法的预测过程可以分为以下几个步骤：

1. 对测试样本进行预测：将测试样本输入每个子模型，得到每个子模型的预测结果。
2. 集成子模型的预测结果：将每个子模型的预测结果进行集成，例如计算平均值或投票等方式，得到最终的预测结果。
3. 输出预测结果：将集成的预测结果输出作为模型对测试样本的预测结果。

需要注意的是，Bagging方法的预测过程与单个模型的预测过程类似，只是其中的模型变成了多个子模型的集成。另外，Bagging方法的预测结果通常比单个模型的预测结果更加稳定和可靠，这也是Bagging方法能够提高模型泛化能力的原因之一。

随机森林（Random Forest， RF）

在Bagging策略的基础上进行修改后的一种算法
• 1. 从原始样本集(n个样本)中用Bootstrap采样(有放回重采样)选出n个样本；
• 2. 使用抽取出来的子数据集(存在重复数据)来训练决策树；从所有属性中随机选择K个属性，从K个属性中选择出最佳分割属性作为当前节点的划分属性，按照这种方式来迭代的创建决策树。
• 3. 重复以上两步m次，即建立m棵决策树；
• 4. 这m个决策树形成随机森林，通过投票表决结果决定数据属于那一类

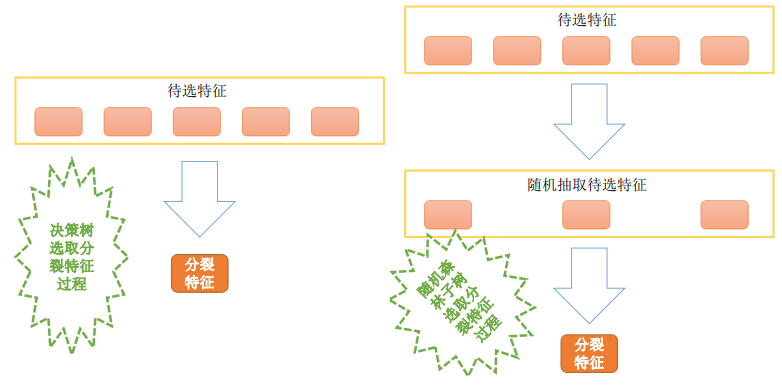
随机森林（Random Forest）是一种基于决策树的集成学习方法。它通过对训练数据进行有放回的随机采样，并随机选择特征来生成多个决策树。随机森林的预测结果是由所有决策树的预测结果进行投票或平均得出的。

随机森林具有以下优点：

1. 随机性：随机森林在生成决策树时通过随机采样和随机选择特征来增加随机性，从而减少了模型的方差，防止了过拟合。
2. 鲁棒性：随机森林可以处理缺失值和不平衡数据，而且对于噪声和异常值也具有较好的鲁棒性。
3. 可解释性：随机森林可以通过对决策树的可视化来解释特征的重要性和模型的决策过程。
4. 高效性：随机森林可以并行化处理，因为每棵决策树的生成是独立的。

随机森林的缺点是它对于高维稀疏数据的效果不如其他模型，而且在某些数据集上可能会过度拟合。此外，如果特征之间存在强相关性，随机森林可能会失去一些性能优势。

RF的推广算法

RF算法在实际应用中具有比较好的特性，应用也比较广泛，主要
应用在：分类、回归、特征转换、异常点检测等。常见的RF变种
算法如下：

• Extra Tree

Extra Trees（极端随机森林）是一种基于决策树的集成学习方法。它与随机森林类似，也是通过对训练数据进行有放回的随机采样来生成多个决策树，并使用投票或平均的方法来组合这些决策树的预测结果。与随机森林不同的是，Extra Trees在生成决策树时采用了更多的随机性。具体来说，Extra Trees在选择特征和切分点时，不仅随机选择特征，而且随机选择切分点，而不是基于特征的重要性或信息增益来选择切分点。这种额外的随机性可以增加模型的多样性，从而降低了模型的方差，提高了模型的泛化能力。Extra Trees在处理高维稀疏数据和噪声数据时表现良好，但在处理低维数据时可能会失去一些性能优势。
这是因为ExtraTree是随机选择特征值的划分点，这样会导致决策树的规模一般大于RF所生成的决策树。ExtraTree模型的方差相对于RF进一步减少。

• Totally Random Trees Embedding(TRTE，完全随机树嵌入)

Totally Random Trees Embedding（完全随机树嵌入）是一种将高维数据映射到低维空间的非线性降维方法。它通过随机生成多棵完全随机树来对原始数据进行编码，并将编码后的数据作为低维特征表示。Totally Random Trees Embedding是一种基于随机森林的降维方法，与传统的随机森林不同的是，它在生成决策树时完全随机地选择特征和切分点，而不是基于特征的重要性或信息增益来选择特征和切分点。由于完全随机树的随机性和多样性，Totally Random Trees Embedding可以更有效地捕捉原始数据的非线性关系和局部结构，从而提高降维的效果。
案例：有3棵决策树，各个决策树的叶子节点数目分别为：5, 5, 4，某个数据x划分到第一个决策树的第3个叶子节点，第二个决策树的第一个叶子节点，第三个决策树的第四个叶子节点，那么最终的x映射特征编码为：（0,0,1,0,0,1,0,0,0,0,0,0,0,1）

• Isolation Forest

孤立森林（Isolation Forest）是一种基于树的异常检测算法，旨在快速识别数据集中的异常点。
孤立森林的基本思想是将正常点和异常点隔离开来。它通过随机选择特征和随机选择切分点来构造一棵二叉树，其中每个节点都是一个切分超平面。对于一个正常点，它很容易被随机切分超平面所划分到较小的区域中，而一个异常点则需要更少的切分次数才能被隔离开来。因此，孤立森林可以通过测量一些异常点被隔离的次数来判断它们是否为异常点。

孤立森林具有以下优点：

1. 高效性：孤立森林的时间复杂度为O(n log n)，比其他基于距离的异常检测方法更快。
2. 鲁棒性：孤立森林对于高维数据和大规模数据都具有很好的鲁棒性。
3. 可扩展性：孤立森林可以在分布式环境下进行并行化处理，从而实现可扩展性。
4. 可解释性：孤立森林可以通过可视化决策树来解释异常点的检测过程。

需要注意的是，孤立森林在处理高度重叠的数据时可能会失去一些性能优势，因为在这种情况下，孤立森林很难将正常点和异常点隔离开来。此外，孤立森林需要调整一些超参数，如树的数量和深度，以获得更好的性能。

对于异常点的判断，则是将测试样本x拟合到m棵决策树上。计算在每棵树上该样本的叶子节点的深度ht(x)。从而计算出平均深度h(x)；然后就可以使用下列公式计算样本点x的异常概率值，p(s,m)的取值范围为[0,1]，越接近于1，则是异常点的概率越大。备注：如果落在的叶子节点为正常样本点，那么当前决策树不考虑，如果所有决策树上都是正常样本点，那么直接认为异常点概率为0.
$p(x,m)=2^{-\frac{h(x)}{c(m)}}$
$$\begin{gathered} c(m)=2ln(m-1)+\xi -2\frac{m-1}{m} \\ m为样本个数，\xi 为欧拉常数 \end{gathered}$$

RF随机森林总结

RF的主要优点： 高效性、随机性、可解释性、高效性
• 1. 训练可以并行化，对于大规模样本的训练具有速度的优势；
• 2. 由于进行随机选择决策树划分特征列表，这样在样本维度比较高的时候，仍然具有比较高的训练性能；
• 3. 给以给出各个特征的重要性列表；
• 4. 由于存在随机抽样，训练出来的模型方差小，泛化能力强，能够缓解过拟合的情况；
• 5. RF实现简单；
• 6. 对于部分特征的缺失不敏感。
RF的主要缺点：
• 1. 在某些噪音比较大的特征上（数据特别异常情况），RF模型容易陷入过拟合；
• 2. 取值比较多的划分特征对RF的决策会产生更大的影响，从而有可能影响模型的效果。

RF scikit-learn相关参数

随机森林的思考

在随机森林的构建过程中，由于各棵树之间是没有关系的，相对独立的；在构建的过程中，构建第m棵子树的时候，不会考虑前面的m-1棵树。 思考：
• 如果在构建第m棵子树的时候，考虑到前m-1棵子树的结果，会不会对最终结果产生有益的影响？

在构建随机森林时，各棵树之间是独立的，构建第m棵子树时不会考虑前m-1棵树的结果。这是随机森林的基本思想，也是随机森林具有高效性和鲁棒性的原因之一。
如果在构建第m棵子树的时候考虑到前m-1棵子树的结果，可能会对最终结果产生一定的影响，但这样做会破坏随机森林的独立性和随机性，可能会导致过拟合和降低模型的泛化性能。因此，在实际应用中，一般不会在构建第m棵子树时考虑前m-1棵子树的结果。

• 各个决策树组成随机森林后，在形成最终结果的时候能不能给定一种既定的决策顺序呢？(也就是那颗子树先进行决策、那颗子树后进行决策)

在形成最终结果时，各个决策树组成的随机森林并没有固定的决策顺序，因为每棵决策树的生成是独立的，它们之间没有先后顺序。在进行预测时，随机森林会同时对每棵决策树进行预测，然后根据投票或平均的方法来组合这些决策树的预测结果。因此，随机森林的预测结果是不受决策树之间的顺序影响的。

元学习法

Boosting

Boosting（提升）是一种集成学习方法，可以用于回归和分类的问题，其基本思想是通过训练多个弱学习器（weak learner）来构建一个强学习器（strong learner）。在Boosting算法中，每个弱学习器都针对先前学习器的错误进行训练，以便最小化误差。在每次迭代中，Boosting算法都会调整样本权重，以便更多地关注先前学习器分类错误的样本。这样，后续学习器将更加关注先前学习器无法正确分类的数据点，从而不断提高整个模型的性能。

常见的Boosting算法包括AdaBoost、Gradient Boosting（GBT/GBDT/GBRT）和XGBoost等。其中，AdaBoost是一种迭代算法，每次训练一个新的弱分类器，然后调整数据的权重，以便将更多的关注点放在先前分类错误的数据上。Gradient Boosting是一种使用残差拟合的迭代算法，每次训练的弱分类器都是在前一次分类器的残差上训练得到的。XGBoost是一种基于Gradient Boosting思想的算法，它使用了一些特殊的技巧来加速训练和提高模型性能。

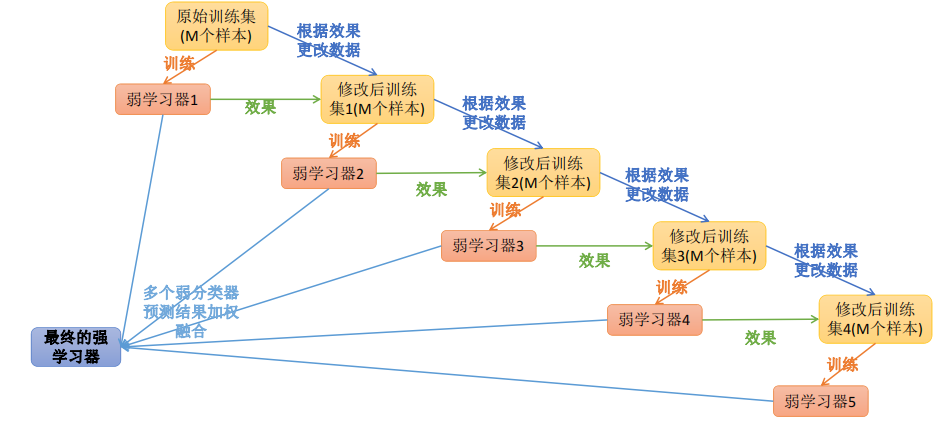
Boosting算法通常具有以下优点：

1. 高准确性：Boosting算法通常可以达到很高的准确性，特别是在处理复杂数据集和高维数据时表现良好。
2. 鲁棒性：Boosting算法可以处理缺失值和不平衡数据，并对噪声数据具有较强的鲁棒性。
3. 可解释性：Boosting算法可以通过可视化每个弱分类器的特征重要性来解释整个模型的决策过程。

需要注意的是，Boosting算法对于噪声数据和异常值敏感，而且训练时间可能会比较长，因为它需要迭代多次来训练弱分类器。此外，Boosting算法也需要调整一些超参数，如学习率、树的深度和树的数量等，以获得更好的性能。

残差拟合（Residual Fitting）

残差（Residual）通常指的是实际值与模型预测值之间的差异或误差。在统计学和机器学习中，我们通常使用残差来评估模型的拟合程度和准确性。
在回归问题中，残差可以定义为：
residual = observed value - predicted value
其中，observed value是实际观测到的数据点，predicted value是模型对该数据点的预测值。残差值越小，则代表模型对数据的拟合程度越好。
在残差拟合中，我们使用前一次迭代的残差来训练下一个弱学习器，以便更好地拟合数据。这是因为残差代表了模型预测值与实际值之间的差异，通过最小化残差，我们可以逐步改进模型的预测能力，从而提高整个模型的性能。
总之，残差是误差的一种特殊形式，它在统计学和机器学习中被广泛使用，用于评估模型的拟合程度和训练下一个弱学习器。

残差拟合（Residual Fitting）是一种基于残差的迭代算法，通常用于Boosting算法中。在Boosting算法中，每个迭代都需要训练一个新的弱学习器（weak learner），以便尽可能地减少前一次迭代的误差。残差拟合的基本思想是，使用前一次迭代产生的残差（即实际值与预测值之间的差异）来训练下一个弱学习器，以便更好地拟合数据。

具体来说，在Boosting算法中，第k个弱学习器的预测值可以表示为：

 $f_k(x)=f_{k-1}(x)+h_k(x)$

其中，$f_{k-1}(x)$表示前k-1个弱学习器的预测值，$h_k(x)$表示第k个弱学习器的预测值。为了最小化预测值与实际值之间的误差，我们可以尝试最小化残差，即：
$r_k=y-f_k(x)$
其中，y表示实际值。因此，第k个弱学习器的训练目标是最小化残差$r_k$。通过这种方式，每个迭代都可以将前一次迭代的误差降到最低，并逐步构建出一个强大的模型。

残差拟合在Gradient Boosting等Boosting算法中被广泛使用。由于残差拟合的基本思想是通过逐步减少误差来构建模型，因此它在处理非线性问题和高维数据时表现良好。

• 残差拟合和梯度下降的思想是相同的吗？

残差拟合（Residual Fitting）和梯度下降（Gradient Descent）是两种不同的算法，但它们的思想是相似的。它们都是迭代算法，通过逐步优化目标函数来优化模型的参数。残差拟合和梯度下降虽然有相似的思想，但它们的具体实现方式和应用场景是不同的。梯度下降通常用于求解函数的最小值或最大值，而残差拟合则用于构建集成学习模型，提高模型的预测能力。

AdaBoost算法

Adaptive Boosting是一种迭代算法。每轮迭代中会在训练集上产生一 个新的学习器，然后使用该学习器对所有训练样本进行预测，以评估每个样本的重要性(Informative)。换句话来讲就是，算法/子模型会为每个样本赋予一个权重，每次用训练好的学习器标注/预测各个样本(训练数据)，**如果某个样本点被预测的越正确，则将样本权重降低；否则提高样本的权重。权重越高的样本在下一个迭代训练中所占的权重就越大，也就是说越难区分的样本在训练过程中会变得越重要（不断提高预测错误样本的权重，使得难区分的样本变得更重要）； **
整个迭代过程直到错误率足够小或者达到一定的迭代次数为止。
Bagging解决的是方差大即过拟合的问题，Adaboost解决的是偏差大即欠拟合的问题。

• Adaboost算法将基分类器的线性组合作为强分类器，同时给分类误差率较小的基本分类器以大的权值，给分类误差率较大的基分类器以小的权重值；构建的线性组合为$f(x)={\sum }_{m=1}^M{\alpha }_m{G}_m(x)，\alpha 为学习器权重$
• 最终分类器是在线性组合的基础上进行Sign函数（符号函数）转换：

$G(x)=sign(f(x))=sign[{\sum }_{m=1}^M{\alpha }_m{G}_m(x)]$

Sign函数

样本加权

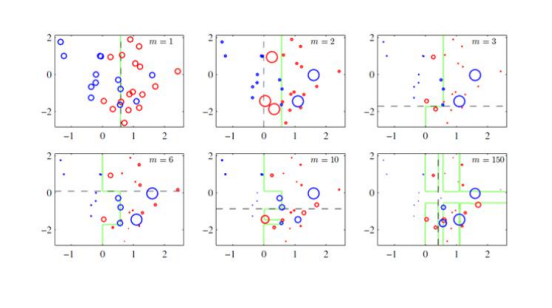
样本加权（Sample Weighting）是一种在机器学习中经常使用的技术，用于处理不平衡数据集或强调某些数据点的重要性。在样本加权中，我们为每个样本分配一个权重，以便在训练模型时更好地平衡数据集或关注某些数据点。

常见的样本加权方法包括：

1. 均衡采样（Balanced Sampling）：对于不平衡的数据集，我们可以从少数类别中随机采样一定数量的数据，以平衡数据集。但这种方法可能会导致信息丢失，因为我们可能会忽略少数类别中的重要数据点。
2. 样本权重调整（Sample Weighting）：我们可以为每个样本分配一个权重，以便在训练模型时更好地关注某些数据点。例如，在处理罕见疾病的数据集时，我们可以将罕见疾病的样本分配更高的权重，以便更好地训练模型。
3. 重采样（Re-sampling）：我们可以通过过采样（Oversampling）或欠采样（Undersampling）来调整数据集的平衡。过采样通常是复制较少类别的数据点，欠采样则是删除较多类别的数据点。但这种方法可能会导致过拟合或信息丢失。

需要注意的是，样本加权并不是适用于所有问题的通用解决方案。在使用样本加权时，我们需要根据实际情况和数据集的特点来选择合适的加权方法和权重分配策略，以便更好地平衡数据集或关注某些数据点。

AdaBoost算法原理

• 最终的强学习器：$G(x)=sign(f(x))=sign[{\sum }_{m=1}^M{\alpha }_m{G}_m(x)]$
• 损失函数（以错误率作为损失函数）：

$$\begin{gathered} {\sum }_{i=1}^n{w}_i=1 \\ loss={\sum }_{i=1}^n{w}_{i}I(G(x_i)\ne y_i)={\sum }_{i=1}^n{w}_i{e}^{(-y_{i}f(x_i))} \end{gathered}$$

• 损失函数（上界）：

$loss={\sum }_{i=1}^n{w}_{i}I(G(x_i)\ne y_i)\le {\sum }_{i=1}^n{w}_i{e}^{(-y_{i}f(x))}$

• 第k-1轮的强学习器：

$f_{k-1}(x)={\sum }_{j=1}^{k-1}{\alpha }_j{G}_j(x)$

• 第k轮的强学习器：

$f_k(x)={\sum }_{j=1}^k{\alpha }_j{G}_j(x)f_k(x)=f_{k-1}(x)+{\alpha }_k{G}_k(x)$

• 损失函数：

l o s s ( α m , G m ( x ) ) = ∑ i = 1 n w 1