leetcode_盛最多水的容器

描述：

给你 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。

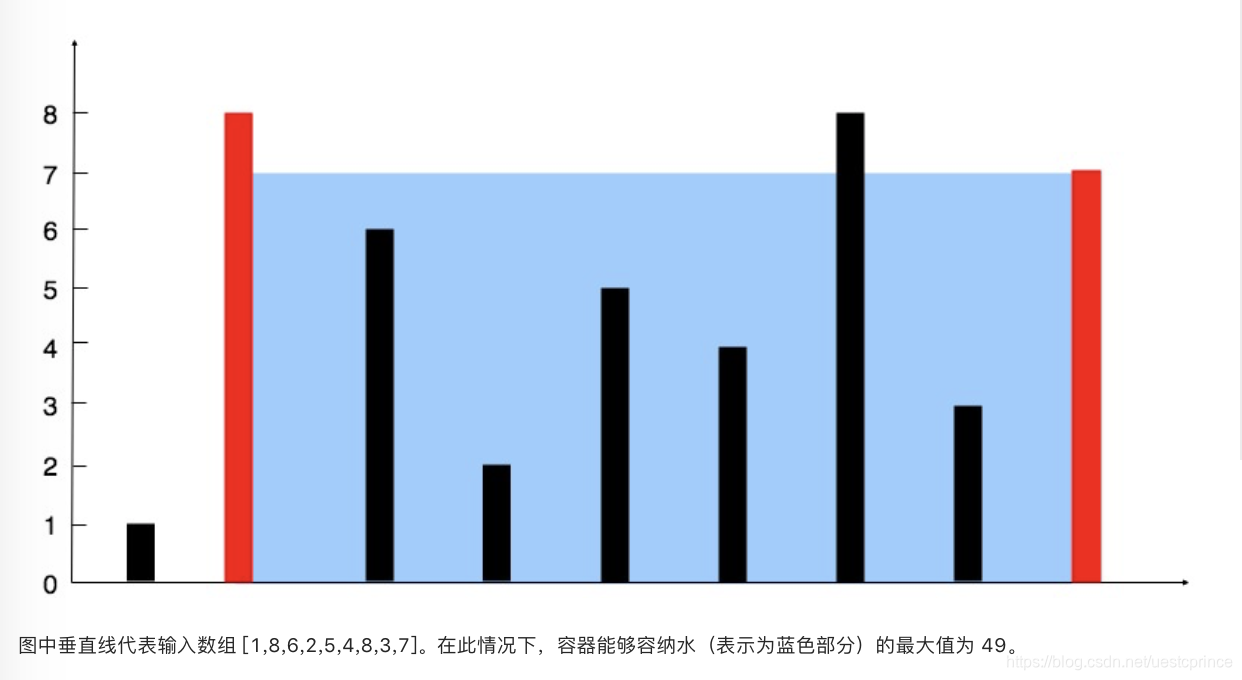
示例：

输入：[1,8,6,2,5,4,8,3,7]
输出：49

解决思路：

用暴力的方式遍历的情况，时间复杂度会达到O（n^2)，如何降低时间复杂度到O（n)?

通过双指针的方式，一个指针指向列表左端，一个指针指向右端，通过调整两个指针以达到最大值，那么如何移动呢？每次移动较小数值的那个指针。

class Solution(object):
    def maxArea(self, height):
        """
        :type height: List[int]
        :rtype: int
        """
        left = 0
        right = len(height) - 1
        maxArea = 0
        while left < right:
            if height[left] > height[right]:
                h = height[right]
                right -= 1
            else:
                h = height[left]
                left += 1
            maxArea = max(maxArea, (right - left + 1)* h)
        return maxArea