2019数据结构考研(二)-----线性表

知识框架

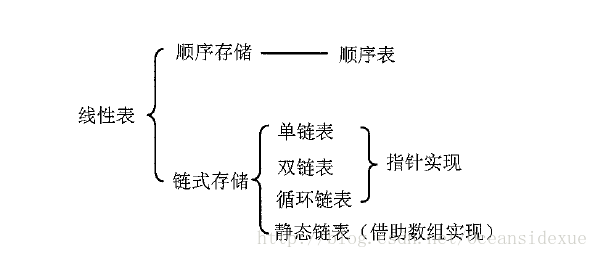
线性表的基本概念

线性表的定义

线性表是具有相同数据类型的n(n>=0)个数据元素的有限序列,n为线性表的表长,当n=0时,则线性表为空表,线性表的第一个元素称为表头,最后一个元素称为表尾

线性表的基本特点

• 线性表的元素个数有上限
• 线性表里的元素具有顺序性
• 表里的元素类型都相同
• 线性表表示一种逻辑上一对一的关系,是逻辑结构,而顺序表和链表则表示一种存储结构,不要混淆
• 表里的元素具有抽象性,即仅仅讨论表里元素之间的逻辑关系,而不讨论表里每个元素的具体内容

线性表的基本操作

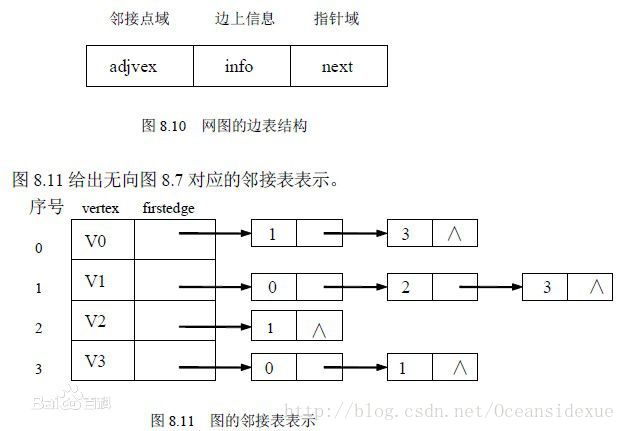
邻接表:存储方法跟树的孩子链表示法相类似，是一种顺序分配和链式分配相结合的存储结构。如这个表头结点所对应的顶点存在相邻顶点，则把相邻顶点依次存放于表头结点所指向的单向链表中。

线性表的顺序表示

线性表的顺序存储称为顺序表,顺序表的特点:表中的元素的逻辑顺序和物理顺序是一致的
线性表中元素的位序从1开始,而数组中元素的下标从0开始的

//c的初始动态分配
L.data=(ElemType*)malloc(sizeof(ElemType)*InitSize)
//c++初始动态分配
L.data=new ElemType[InitSize] 

特点:随机访问,存储密度高,只存储数据元素,逻辑上相邻的元素在物理上也相邻

顺序表的插入操作

bool ListInsert(Sqlist &L,int i,ElemType e){
    if(i<1||i>L.length+1)//判断i的范围是否有效 
    return false;
    if(L.length>=MaxSize)//判断表的存储空间是否已满
    return false;
    for(int j=L.length;j>=i;j--){
        //将i后的元素往后移动
        L.data[j]=L.data[j-1]; 
    } 
    L.data[i-1]=e;//将元素e插入i位置 
    L.length++;
    return true; 
}

判断i是否有效时,i>length+1,i可以是插在表尾
最好的情况:在表尾插入,不移动元素,时间复杂度为O(1)
最坏的情况:在表头插入.都要移动,时间复杂度为O(n)
平均情况:pi为概率pi=1/(1+n),有n+1个位置可以插入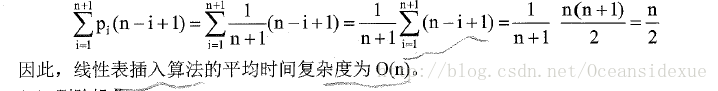

顺序表的删除操作

bool ListDelete(Sqlist &L,int i,ElemType e){
    //本算法实现删除顺序表中第i个元素 
    if(i<1||i>L.length+1)//判断i的范围是否有效 
    return false;
    e=L.data[i-1];//将被删除的元素赋值给e 
    for(int j=i;j<length;j++){
        //将i后的元素往后移动
        L.data[j-1]=L.data[j]; 
    } 
    L.length--;
    return true; 
}

顺序表的按值查找

int LocateElem(Sqlist L,ElemType e){
    //本算法实现查找顺序表里值为e的元素,成功返回位值,否则返回0
    int i;
    for(i=0;i<L.length;i++){
        if(L.data[i]==e)//下标为i的的元素为e,返回其位序i+1 
        return i+1;
    } 
    return 0;
} 

单链表

typedef struct LNode{
    ElemType data;//数据域存放数据元素
    struct LNode *next; //指针域 ,存放下一个结点的地址
}LNode,*LinkList;

头结点和头指针的区别

• 无论有没有头结点,头指针都指向链表的第一个结点,通常用头指针来表示一个链表L
• 头结点,结点内通常不存储元素,有头结点的话,头指针都指向一个非空链表
  ##单链表的基本操作实现
  ###头插法建立单链表

typedef struct LNode{
    ElemType data;//数据域 
    struct LNode *next; //指针域 
}LNode,*LinkList;

LinkList CreateList1(LinkList &L){
    LNode *s;
    int x;
    L->next=null;//初始为空链表 
    scanf("%d",&x); 
    while(x!=9999)//输入9999表示结束
    {
        s=(LNode*)malloc(sizeof(LNode));//创建新结点 
        s-data=x;
        s->next=L->next;
        L->next=s;//新结点插入到链表中,L为头指针 
        scanf("%d",&x);
    } 
}

LNode,*LinkListl，都是匿名结构体别名，Lnode是实体，而LiskList是这种ElemType类型的指针
malloc是动态开辟内存,函数返回为void型指针(指向开辟的内存空间)
前面那个括号是开辟内存的类型,如L=(linklist*)malloc(sizeof(lnode)),就是将原来malloc返回的void型指针强制定义为 linklist型(也就是你一开始定义的指针L的类型),这样才可以赋值给L.
sizeof(Inode)是指malloc开辟的内存空间的大小,这里就是指,这个大小为Inode型所占的容量.(例如sizeof(int),就是开辟一个整形的空间(4字节).分配两个int的空间就是2*sizeof(int))

尾插法建立单链表

LinkList CreateList2(LinkList &L){
    L=(LinkList)malloc(sizeof(LNode)); 
    LNode *s,*r=L;//r为表尾指针 
    int x;  
    scanf("%d",&x); 
    while(x!=9999)//输入9999表示结束
    {
        s=(LNode*)malloc(sizeof(LNode));//创建新结点 
        s-data=x;
        r->next=s->next;
        r=s;//r指向新的表尾结点 
        scanf("%d",&x);
    } 
    r->next=null;//尾结点置空 
    return L; 
}

按序号查找结点

LNode *GetElemt(LinkList L,int i){
    //该算法取出链表中i位置的结点指针
    int j=1;
    LNode *p=L->next;
    if(i==0)
    return L;
    if(i<1)
    return null; 
    while(p&&j<i){
        p=p->next;
        j++;
    }
    return p;//如果i大于表长,p=null 
}

时间复杂度为O(n)

单链表的插入操作

前插法

p=GetElemt(L,i-1)//获得i的前驱结点
s->next=p->next;
p->next=s; 

时间复杂度为O(1)
顺序不能颠倒
也可以转化成后插法,先进行前插,再将两个的数据进行交换

删除结点操作

p=GetElemt(L,i-1)//获得i的前驱结点
q=p->next;//q指向被删除结点
p->next=q->next;
free(q);//释放q 结点 

时间复杂度为O(1)

双链表

双链表在单链表的基础上增加了一个结点,有一个前驱结点prior,有一个后继结点next

typedef struct DNode{
    ElemType data;//数据域 
    struct DNode *next,*prior;//前驱和后继结点 
}DNode,*DLinkList; 

插入和删除的时间复杂度为O(1)

双链表的插入操作

在双链表指针p后面插入结点s

s->next = p->next;//1
p->next->prior=s;//2
p->next=s;//3
s->prior=p;//4

1,2两步必须在3之前

双链表的删除操作

//删除q结点
p->next=q->next;
q->next->proir=p; 

循环链表

循环链表与单链表的区别在于最后一个结点不为空,而改成指向头结点

顺序表和链表的比较

• 存取方式:顺序表为随机存取,而链表为顺序存取
• 逻辑结构和物理结构:顺序存储时,逻辑上相邻的元素在物理结构上也相邻,而链表存储时,物理结构上不一定相邻
• 查找,删除和插入操作:对于按值查找,在顺序表无序时,两者的时间复杂度都为O(n),当顺序表有序时可以采用折半查找,顺序表的时间复杂度为O(log2n),对于按序号查找,顺序表的时间复杂度为O(1),而链表时间复杂度为O(n)
• 空间分配:链表可以在需要时申请分配,只要内存有空间就可以进行分配,高效灵活

 

本文转载自:https://blog.csdn.net/Oceansidexue/article/details/79321059