《算法导论》第四章-第4节_练习（参考答案）

算法导论（第三版）参考答案：练习4.4-1，练习4.4-2，练习4.4-3，练习4.4-4，练习4.4-5，练习4.4-6，练习4.4-7，练习4.4-8，练习4.4-9

Exercise 4.4-1

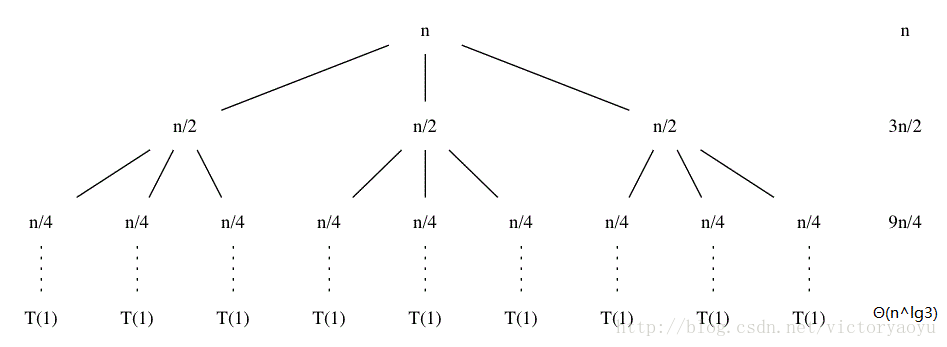
Use a reccursion tree to determine a good asymptotic upper bound on the recurrence $T(n)=3T(⌊n/2⌋)+n$. Use the substitution method to verify your answer.

假设 $n$ 是2的幂（忍受不精确），则递归树为

注：请看更正版，一个更好的渐进紧确界。

树高 $\lg{n}$，叶节点数量为 $3^{\lg{n}}=n^{\lg{3}}$，整棵树的代价：

$$\begin{align} T(n) &= n+(\frac{3}{2})n+(\frac{3}{2})^2n+ \cdots + (\frac{3}{2})^{\lg{n}-1}n+ \Theta(n^{\lg{3}}) \\ &= \sum_{i=0}^{\lg{n}-1}\Big(\frac{3}{2}\Big)^i n + \Theta(n^{\lg3}) \\ &= n\frac{(3/2)^{\lg{n}} - 1}{(3/2) - 1} + \Theta(n^{\lg3}) \\ &\lt n\frac{(3/2+1/2)^{\lg{n}} - 1}{(3/2) - 1} + \Theta(n^{\lg3}) \\ &\lt n\frac{n - 1}{(3/2) - 1} + \Theta(n^{\lg3}) \\ &= O(n^2) \end{align}$$
代入法证明 $T(n) \le cn^{2}+2n$ :
$$\begin{align} T(n) & \le 3c(n/2)^{2} + 2 \cdot n/2 + n \\ &= \frac{3}{4}cn^{2} + 2n \\ &\le cn^2 + 2n \\ \end{align}$$
$O(n^2)$ 为 $T(n)$ 的一个渐进上界。

更正：

$$\begin{align} T(n) &= n+(\frac{3}{2})n+(\frac{3}{2})^2n+ \cdots + (\frac{3}{2})^{\lg{n}-1}n+ \Theta(n^{\lg{3}}) \\ &= \sum_{i=0}^{\lg{n}-1}\Big(\frac{3}{2}\Big)^i n + \Theta(n^{\lg3}) \\ &= n\frac{(3/2)^{\lg{n}} - 1}{(3/2) - 1} + \Theta(n^{\lg3}) \\ &= 2n(\frac{3^{\lg{n}}}{n}-1) + \Theta(n^{\lg3}) \\ &= 2 \cdot 3^{\lg{n}}-2n + \Theta(n^{\lg3}) \\ &= O(n^{\lg(3)}) \end{align}$$
代入法证明 $T(n) \le cn^{\lg{3}}+2n$ :
$$\begin{align} T(n) & \le 3c(n/2)^{\lg{3}} + 2 \cdot n/2 + n \\ &= cn^{\lg{3}} + 2n \\ &= O(n^{\lg{3}}) \\ \end{align}$$