题意:
找两个字符串的最长公共子序列(Loggest Common Subsequence, LCS)。用“表格法”(姑且这么叫吧)就可以很快地做出来,至于表格法的原理,以后有时间再整理吧,一时半会也整理不出来。
比如给出的第一组输入:
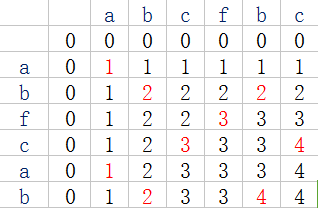
具体的转移方程是:
// dp[i][j]表示在到了字符串sa的i位置和字符串sb的j位置时,可以达到的最大值,因为这里做了一个第一行列为0的初始化,所以对应到字符串时,下标要减去1
if (str_a[i-1] == str_b[j-1]) {
dp[i][j] = 1 + dp[i-1][j-1];
} else {
dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
}代码(78ms, 5692KB):
#include <iostream>
#include <cstring> // memset
#include <string>
#include <algorithm> // max
using namespace std;
const int maxn = 1001;
int dp[maxn][maxn];
int main() {
// freopen("in.txt", "r", stdin);
string sa, sb;
while (cin >> sa >> sb) {
memset(dp, 0, sizeof dp);
int la = sa.size(), lb = sb.size();
for (int i = 1; i <= la; ++i) {
for (int j = 1; j <= lb; ++j) {
if (sa[i-1] == sb[j-1]) {
dp[i][j] = 1 + dp[i-1][j-1];
} else {
dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
}
}
}
cout << dp[la][lb] << endl;
}
return 0;
}思考:
如果是多个字符串,又怎么处理呢?






















 284
284

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








