机器学习（5）多项式回归：用基函数扩展线性模型

机器学习中的一个常见模式是使用数据的非线性函数训练的线性模型。 这种方法保持了线性方法的一般快速的性能，同时允许它们适应更宽范围的数据。

例如，可以通过从系数构建多项式特征来扩展简单的线性回归。 在标准线性回归情况下，对于二维数据，您可能有一个类似于下面的模型：

如果我们想要将抛物面拟合到数据而不是平面，我们可以组合二阶多项式中的特征，使得模型看起来像这样：

（有时令人惊讶的）观察是，这仍然是一个线性模型：看到这一点，想象创建一个新的变量

通过这种重新标记的数据，我们的问题可以写

我们看到，所得到的多项式回归是在我们上面考虑的同一类线性模型中（即模型在w中是线性的），并且可以通过相同的技术来求解。 通过考虑使用这些基函数构建的更高维空间内的线性拟合，该模型具有适应更宽范围的数据的灵活性。

这里是一个应用这个想法到一维数据，使用不同程度的多项式特征的例子：

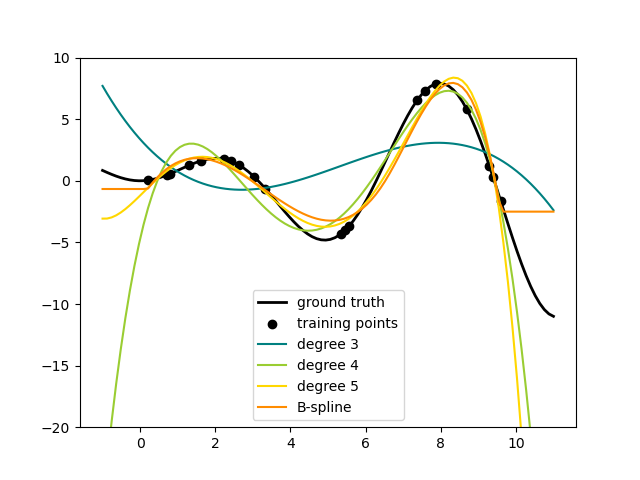
此图是使用PolynomialFeatures预处理器创建的。 该预处理器将输入数据矩阵变换为给定度的新数据矩阵。 它可以如下使用：

>>> from sklearn.preprocessing import PolynomialFeatures
>>> import numpy as np
>>> X = np.arange(6).reshape(3, 2)
>>> X
array([[0, 1],
       [2, 3],
       [4, 5]])
>>> poly = PolynomialFeatures(degree=2)
>>> poly.fit_transform(X)
array([[  1.,   0.,   1.,   0.,   0.,   1.],
       [  1.,   2.,   3.,   4.,   6.,   9.],
       [  1.,   4.,   5.,  16.,  20.,  25.]])

X的特征已经从变换到，现在可以在任何线性模型中使用。

这种预处理可以用流水线（ Pipeline）工具简化。 表示简单多项式回归的单个对象可以被创建并使用如下：

>>> from sklearn.preprocessing import PolynomialFeatures
>>> from sklearn.linear_model import LinearRegression
>>> from sklearn.pipeline import Pipeline
>>> import numpy as np
>>> model = Pipeline([('poly', PolynomialFeatures(degree=3)),
...                   ('linear', LinearRegression(fit_intercept=False))])
>>> # fit to an order-3 polynomial data
>>> x = np.arange(5)
>>> y = 3 - 2 * x + x ** 2 - x ** 3
>>> model = model.fit(x[:, np.newaxis], y)
>>> model.named_steps['linear'].coef_
array([ 3., -2.,  1., -1.])

在多项式特征上训练的线性模型能够精确地恢复输入多项式系数。

在某些情况下，不需要包括任何单个特征的更高的指数，而只需要将最多d个不同特征相乘的所谓的相互作用特征。 这些可以从PolynomialFeatures设置interaction_only=True获得。

例如，当处理布尔特征时，对于所有n，，因此是无用的; 但表示两个布尔的“且”。 这样，我们可以使用线性分类器解决异或（XOR）问题：

>>> from sklearn.linear_model import Perceptron
>>> from sklearn.preprocessing import PolynomialFeatures
>>> import numpy as np
>>> X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
>>> y = X[:, 0] ^ X[:, 1]
>>> y
array([0, 1, 1, 0])
>>> X = PolynomialFeatures(interaction_only=True).fit_transform(X).astype(int)
>>> X
array([[1, 0, 0, 0],
       [1, 0, 1, 0],
       [1, 1, 0, 0],
       [1, 1, 1, 1]])
>>> clf = Perceptron(fit_intercept=False, n_iter=10, shuffle=False).fit(X, y)

分类器“预测”是完美的：

>>> clf.predict(X)
array([0, 1, 1, 0])
>>> clf.score(X, y)
1.0