hdu 3507 Print Article 斜率优化dp

【题目大意】
零有一个旧打印机，有时不能很好的工作。因为它是古董，所以零仍然喜欢用它来打印物品。但打印机太老了，工作了很长一段时间肯定会磨损，所以零使用成本来评估这个程度。
一天零想打印一篇有n单词的文章，每个单词i都有一个成本ci。此外，零知道打印k个单词在一行将成本为
M是一个常量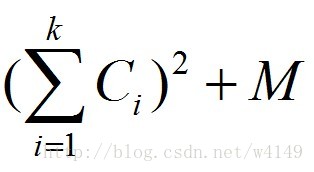
现在零想知道打印的最低成本。
0 ≤ n ≤ 500000, 0 ≤ M ≤ 1000

稍微思索一番，就可以得出转移方程
dp[i] = dp[j] + ( sum[i] - sum[j] ) ^ 2 + m
本来应 for 一遍 i，for 一遍 j，复杂度为 O（n^2），为了降次，就需要用到斜率优化维护最优的 j，
不妨设 j，k 且 j < k，那么
dp[i] = dp[j] + ( sum[i] - sum[j] ) ^ 2 + m，dp[i] = dp[k] + ( sum[i] - sum[k] ) ^ 2 + m,
dp[i]应当从较小的地方转移过来，于是
dp[j] + ( sum[i] - sum[j] ) ^ 2 + m < dp[k] + ( sum[i] - sum[k] ) ^ 2 + m
化简后得 dp[j] + sum[j] ^ 2 - dp[k] - sum[k] ^ 2 < 2 * sum[i] * ( sum[j] - sum[k] )
（ dp[j] + sum[j] ^ 2 - dp[k] - sum[k] ^ 2 ） / 2 * sum[j] - 2 * sum[k] > sum[i] ……【1】
斜率优化题目中分母( sum[j] - sum[k] )往往是负数，移项后要变号。

即如果有一组 j，k 满足这一个关系式，那么就说明 j 更优，反之 k 更优。

那么为什么不能就单纯地通过这个不等式维护一个单调队列呢？（谁不优就把谁删掉）
这是我最开始走入的一个误区，我们在最外层for了一遍i，所以说我们的（sum[i]）是会变化的，
也就是说有可能这一次 j 比 k 优，下一次就是 k 比 j 优了。所以贸然删除一个点是不科学的。
单单是通过这样一个关系式，我们是无法构造出一个单调关系的。

所以我们再来观察一下这个式子，
（ dp[j] + sum[j] ^ 2 - dp[k] - sum[k] ^ 2 ） / 2 * sum[j] - 2 * sum[k] > sum[i]
形如 （ Ay - By ） / （Ax - Bx） > M ，这样看左边就是一个斜率表达式了，
因为 j < k < i 所以dp[j],dp[k],sum[j],sum[k]都是已知的，就是说x与y坐标都定下来了，
两点之间的斜率也就固定了，我们怎么来吧斜率和单调联系起来呢？

假设q队列里面的元素为a1,a2,a3…an,我们想要的状态是a1优于a2优于a3…优于an，
也就是说要让 k(a1,a2)>M,k(a2,a3)>M,k(a3,a4)>M…我们自然不可能一个一个的判断,
所以容易想到让 M < k(a1,a2) < k(a2,a3) < k(a3,a4)…这样把斜率按照从小到大排个序，head自然就最优了。
由此提出解决方案，维护一个下凸包，当然如果不等号反向就是上凸包了。

易证，如果一个点不在维护的凸包上面，那么他一定不是最优的

#include <iostream>  
#include <cstdio> 
#include <cstring>
#include <algorithm>
#define LL long long 
using namespace std;  

const int N = 500010;  
int n, m;
int dp[N], q[N], sum[N];

int pointx(int i , int j){  
    return 2 * (sum[i] - sum[j]);  
} 

int pointy(int i , int j){  
    return sum[i] * sum[i] + dp[i] - (sum[j] * sum[j] + dp[j]);  
}

int main(){  
    int cc;
    while( ~scanf("%d%d", &n, &m) ){  
        int head = 0, tail = 0;  
        q[tail++] = 0;
        for(int i=1; i<=n; i++){ 
            scanf("%d", &cc);  
            sum[i] = sum[i-1] + cc;  
            while(head + 1 < tail && pointy(q[head+1] ,q[head]) <= pointx(q[head+1], q[head]) * sum[i]) ++head;
            //a1不比a2优，head++，直到满足head最优 
            dp[i] = (sum[i] - sum[q[head]]) * (sum[i] - sum[q[head]]) + m + dp[q[head]];
            while(head + 1 < tail && pointy(i, q[tail-1]) * pointx(q[tail-1], q[tail-2]) <= pointy(q[tail-1], q[tail-2]) * pointx(i, q[tail-1])) --tail; 
            //维护下凸包 
            q[tail++] = i;   
        } 
        printf("%d\n", dp[n]);  
    }  
    return 0;  
}