在做摩擦力辨识中,因为需要用对非线性模型的参数进行辨识,在上一篇博客中使用了非线性最小二乘的辨识方法,但是其辨识结果的精准度受辨识参数初值的选取影响很大,很容易陷入局部最优解,而不能得到全局最优解,所以使用遗传算法来进行辨识,遗传算法是可以得到全局最优解的。
最开始是自己编写的遗传算法程序来进行辨识,但是得到的结果有些瑕疵,所以尝试使用MATLAB工具箱来做一次。下面是入门使用的方法(MATLAB版本是201b):
1. 打开MATLAB遗传算法工具箱:(1)点击状态栏的APP;(2)找到Optimization并打开,如下图所示:
在Solver后面的下拉框中,选择遗传算法:ga-Genetic Algorithm,下边分别就遗传算法的几个步骤进行说明。

2. fitness function 适应度函数
在学习遗传算法后我们知道中间一个步骤是需要确定适应度函数,而适应度函数一般是通过目标函数转换而来,在一些解决函数最大值和最小值的问题中,可以直接把函数输出作为目标函数和适应度函数。经过测试验证,在改工具箱中,适应度函数的输出结果越小标明越准确。下面介绍摩擦力模型及适应度函数:
我要辨识的摩擦力模型为:

需要辨识其中的 A,B,C 和 D 四个参数,通过实验采集到的实际输入数据 v 和输出数据 F。因为工具箱要求的适应度函数是输出结果趋小的,所以我这里选择目标函数为适应度函数,如下:

其中

为辨识误差。
将该目标函数以函数的形式写到 MATLAB 的m文件中,如下:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 | % 使用遗传算法工具箱的适应度函数function result = steadyfitness(a) load SteadyData.mat; u = (up+abs(un))/2/4; Fi =u'; % 均匀实验测得摩擦力的实测值 w = vd'; % 速度输入值 N = size(w,1); for i = 1:1:N F_GA(i) = (a(1)+a(2)*exp(-(w(i)/a(3))^2))*sign(w(i)) + a(4)*w(i); Ji(i) = Fi(i) - F_GA(i); J(i) = 0.5*Ji(i)*Ji(i); end result = sum(J);end |
而后将函数句柄 “@steadyfitness" 写到工具箱界面的 fitness function 后面。
3. Number of variables:输入参数个数
这里待辨识参数有A,B,C和D这四个,所以这里填写 4。
4. bounds:辨识参数的上下界
此处设置为,Lower:[0 0 0 0],Upper:[0.5 0.5 0.1 0.5]。
5. 点击 Start,开始遗传算法求解
结束后结果会显示在 Final point中
下图见完整的配置:

6. 利用辨识参数的结果,绘制摩擦力模型

完结。
注:MATLAB工具箱的简单使用,上述几个步骤就够用了,如果要修改默认算法部分,就要学习遗传算法原理,修改工具箱右侧的参数。
2. fitness function 适应度函数
在学习遗传算法后我们知道中间一个步骤是需要确定适应度函数,而适应度函数一般是通过目标函数转换而来,在一些解决函数最大值和最小值的问题中,可以直接把函数输出作为目标函数和适应度函数。经过测试验证,在改工具箱中,适应度函数的输出结果越小标明越准确。下面介绍摩擦力模型及适应度函数:
我要辨识的摩擦力模型为:

需要辨识其中的 A,B,C 和 D 四个参数,通过实验采集到的实际输入数据 v 和输出数据 F。因为工具箱要求的适应度函数是输出结果趋小的,所以我这里选择目标函数为适应度函数,如下:
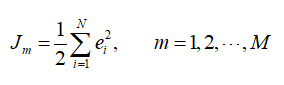
其中

为辨识误差。
将该目标函数以函数的形式写到 MATLAB 的m文件中,如下:
% 使用遗传算法工具箱的适应度函数
function result = steadyfitness(a)
load SteadyData.mat;
u = (up+abs(un))/2/4;
Fi =u'; % 均匀实验测得摩擦力的实测值
w = vd'; % 速度输入值
N = size(w,1);
for i = 1:1:N
F_GA(i) = (a(1)+a(2)*exp(-(w(i)/a(3))^2))*sign(w(i)) + a(4)*w(i);
Ji(i) = Fi(i) - F_GA(i);
J(i) = 0.5*Ji(i)*Ji(i);
end
result = sum(J);
end
而后将函数句柄 “@steadyfitness" 写到工具箱界面的 fitness function 后面。
3. Number of variables:输入参数个数
这里待辨识参数有A,B,C和D这四个,所以这里填写 4。
4. bounds:辨识参数的上下界
此处设置为,Lower:[0 0 0 0],Upper:[0.5 0.5 0.1 0.5]。
5. 点击 Start,开始遗传算法求解
结束后结果会显示在 Final point中
下图见完整的配置:

6. 利用辨识参数的结果,绘制摩擦力模型

完结。
注:MATLAB工具箱的简单使用,上述几个步骤就够用了,如果要修改默认算法部分,就要学习遗传算法原理,修改工具箱右侧的参数。























 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








