HDU 1159 Common Subsequence(动态规划）

最新推荐文章于 2024-10-01 18:52:56 发布

wadye

最新推荐文章于 2024-10-01 18:52:56 发布

阅读量302

点赞数

文章标签：动态规划

欢迎转载评论，求点赞关注加收藏，蟹蟹。

本文链接：https://blog.csdn.net/wadye/article/details/47661979

版权

题目链接：Click here

题意：现在给出两个序列a 和b，找到a 和b 的最大公共子序列

思路：通过一组数据看一下：
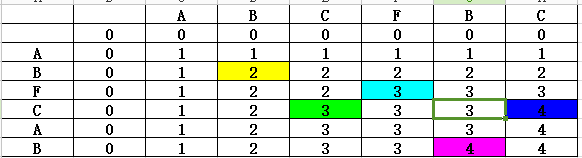
这里写图片描述
在这组数据中，所有带颜色的地方，均为字符相等的地方，通过观察可以发现，如果某处字符相等，那么它的值就是它右上角的值加一，否则就是其左边和上边的最大值。
那么状态转换方程就可以得出：
如果a[i] == b[i]
dp[i][j] = dp[i-1][j-1] + 1;
否则
dp[][j] = max(dp[i-1][j], dp[i][j-1]);

具体看代码：

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>

using namespace std;

char a[1001], b[1001];
int dp[1001][1001];

int main()
{
    int str1, str2;
    while(scanf("%s%s", a+1, b+1) != EOF) //字符串从1开始，这样不用判断边界问题
    {
        str1 = strlen(a+1);
        str2 = strlen(b+1);
        for(int i = 0; i <= str1; i++)
            dp[i][0] = 0;  //初始化，从0开始，不用考虑边界问题
        for(int i = 0; i <= str2; i++)
            dp[0][i] = 0;
        for(int i = 1; i <= str1; i++)
        {
            for(int j = 1; j <= str2; j++)
            {
                if(a[i] == b[j])
                    dp[i][j] = dp[i-1][j-1] + 1;
                else
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
            }
        }
        printf("%d\n", dp[str1][str2]);
    }
    return 0;
}