最大子列和问题

给定K个整数组成的序列{ N₁, N₂, ..., N_K }，“连续子列”被定义为{ N_i, N_i+1, ..., N_j }，其中 1 <= i <= j <= K。“最大子列和”则被定义为所有连续子列元素的和中最大者。例如给定序列{ -2, 11, -4, 13, -5, -2 }，其连续子列{ 11, -4, 13 }有最大的和20。现要求你编写程序，计算给定整数序列的最大子列和。

输入格式：

输入第1行给出正整数 K (<= 100000)；第2行给出K个整数，其间以空格分隔。

输出格式：

在一行中输出最大子列和。如果序列中所有整数皆为负数，则输出0。

输入样例：

6
-2 11 -4 13 -5 -2

输出样例：

20

方法一：时间复杂度O(n^3)

#include <iostream>
#include <cstdio>
using namespace std;


int a[100005];


int Maxsum(int *a, int n)
{
    int max,thisum;
    max =  0;
    for (int i = 0; i < n; i++)
    {


        for (int j = i; j < n; j++)
        {
            thisum = 0;
            for (int k = i; k <= j; k++)
            {
                thisum += a[k];
            }
            if (thisum > max)
            {
                max = thisum;
            }
        }
    }
    return max;
}
int main()
{
    int k;
    while (cin >> k && k)
    {
        for (int i = 0; i < k; i++)
        {
            scanf("%d",&a[i]);
        }
        cout << Maxsum(a,k)<< endl;
    }
    return 0;
}

方法二：时间复杂度O(n^2),在法一我们可以改进，k不是必要的。

#include <iostream>
#include <cstdio>
using namespace std;

int a[100005];

int Maxsum(int *a, int n)
{
    int max,thisum;
    max = 0;
    for (int i = 0; i < n; i++)
    {
        thisum  = 0;
        for (int j = i; j < n; j++)
        {
            thisum += a[j];
            if (thisum > max)
            {
                max = thisum;
            }
        }
    }
    return max;
}
int main()
{
    int k;
    while (cin >> k && k)
    {
        for (int i = 0; i < k; i++)
        {
            scanf("%d",&a[i]);
        }
        cout << Maxsum(a,k)<< endl;
    }
    return 0;
}

方法三：时间复杂度O(nlogn)

在法二里，我们可以想办法再改进，将O(n^2)改为O(nlogn)，这我们就想到了分治法。（先放一下，有时间写）

在这里，我们可以将序列分成两部分left,right，那么可能有以下三种情况：

1.最大值在左边left.

2.最大值在右边right.

3.最大值横跨左右两边。

如下如：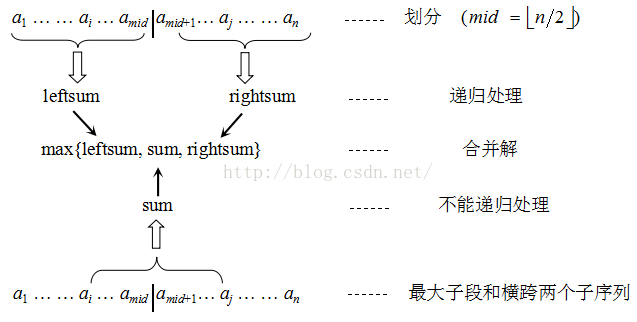

int MaxSum(int a[ ], int left, int right)
{
       sum=0;
       if (left= =right) {      //如果序列长度为1，直接求解
           if (a[left]>0) sum=a[left];
           else sum=0;
       }
      else {
          center=(left+right)/2;    //划分
          leftsum=MaxSum(a, left, center);   //对应情况1，递归求解
          rightsum=MaxSum(a, center+1, right); //对应情况2，递归求解
           s1=0; lefts=0;              //以下对应情况3，先求解s1
        for (i=center; i>=left; i--)
        {
            lefts+=a[i];
            if (lefts>s1) s1=lefts;
        }
        s2=0; rights=0;             //再求解s2
        for (j=center+1; j<=right; j++)
        { 
            rights+=a[j];
            if (rights>s2) s2=rights;
        }
        sum=s1+s2;              //计算情况3的最大子段和 
        if (sum<leftsum) sum=leftsum;  
                     //合并，在sum、leftsum和rightsum中取较大者
        if (sum<rightsum) sum=rightsum;
     }
     return sum;
}

方法四：时间复杂度O(N)---最快的。

思路：thisum记录当前子序列的和，值要它小于0，则重置为0，耶就是重头来过，因为前面的子序列小于0，绝对会使后面的和减小，这不是我们要的。

#include <iostream>
#include <cstdio>
using namespace std;

int a[100005];

int Maxsum(int *a, int n)
{
    int max ,thisum;
    max = thisum  = 0;
    for (int i = 0; i < n; i++)
    {
        thisum += a[i];
        if (thisum > max)
        {
            max = thisum;//更新max
        }
        if (thisum < 0)
        {
            thisum = 0;//重置过程
        }
    }
    return max;
}
int main()
{
    int k;
    while (cin >> k && k)
    {
        for (int i = 0; i < k; i++)
        {
            scanf("%d",&a[i]);
        }
        cout << Maxsum(a,k)<< endl;
    }
    return 0;
}