学习《算法导论》第一章 插入排序 总结

学习《算法导论》第一章 插入排序 总结

---

1. 算法入门

1.1 算法简介

an Algorithm is any well-defined computational procedure that
takes some value, or set of values, as input and produces some
value, or set of values, as output. An algorithm is thus a sequence of
computational steps that transform the input into the output.
—–《Introduction to Algorithms》

1.2 算法分析

算法分析就是指对一个算法所需要的资源进行预测. 通常，资源是指我们希望测度的计算时间. 在分析一个算法之前，要建立有关实现技术的模型，包括描述所用资源的及代价的模型.
本书我们采用一种通用的单处理器、随机存取机(RAM)计算模型来作为我们的实现技术. 在RAM模型中，指令一条接一条的执行，没有并发操作.
一般来说，算法所需的时间是与输入规模同步增长的，因而常将一个程序的运行时间表示为输入的函数.

1.2.1 最坏情况分析

一般来说，我们都是考察算法的最坏情况运行时间，即对于规模为n的任何输入，算法的最长运行时间. 这样做的理由有三点：
a. 一个算法的最坏情况运行时间是在任何输入下运行时间的一个上界. 这样，就能确保算法的运行时间不会比这一时间更长.
b. 对于某些算法，最坏情况出现得相当频繁.
c. 大致来看，平均情况通常与最坏情况一样差.
如果一个算法的最坏情况运行时间要比另一个算法的低，我们就认为它的效率更高.

2.插入排序

2.1 插入排序的思想

插入排序的思想是增量方法：在排好子数组A[1…j-1]后，将元素A[j]插入，形成排好序的子数组. 如下图：

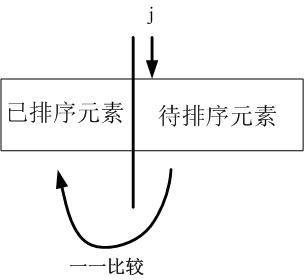
知道这个了，插入排序的算法很好实现了.

2.2 插入排序算法

INSERTION-SORT(A)
1    for j ← 2 to length[A]
2        do key ← A[j]
3        ►将A[j]插入已排序数组A[1…j-1]
4        i ← j – 1
5        while i > 0 and A[i] > key
6            do A[i+1] ← A[i]
7               i—
8        A[i+1] ← key

2.3 插入排序时间复杂度分析

具体分析略，可以参考书. 排入排序的最坏情况时间代价为Θ(n2). 从算法上来也容易理解，for循环里面一个while循环.

2.4 插入排序代码实现

void InsertSort(int* SortArray, int length)
{
    int pWaitSort = 0;
    int pSorted = 0;
    int key = 0;

    for (pWaitSort = 1; pWaitSort < length; pWaitSort++)
    {
         key = SortArray[pWaitSort];
         pSorted = pWaitSort – 1;
         while ((pSorted >= 0) && (SortArray[pSorted] < key))
         {
              SortArray[pSorted+1] = SortArray[pSorted];
              pSorted--;
         }
           SortArray[pSorted++] = key;
    }

      return;
}