Digimat-MF：平均场均匀化——（四）分布方向和方向分布函数

【未经许可，不得转载！】

　　在实际的短纤维增强复合材料RVE中，纤维是杂乱的，如图 1.7所示。



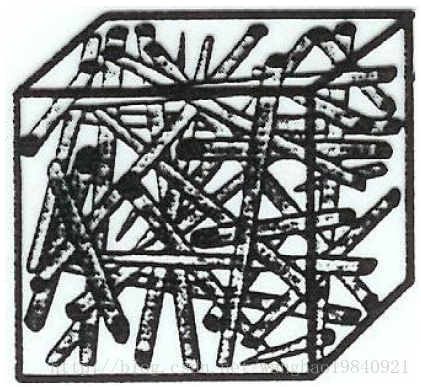
图1.7 RVE中杂乱的短纤维

　　首先引入一些工具来描述纤维方向。以下描述不仅限于纤维，还可应用于回转椭球体。每个夹杂体的方向用单位向量 $\mathbf{p}$来描述，在三维空间表述为两个球角度 $\theta$和 $\phi$，如图 1.8所示。



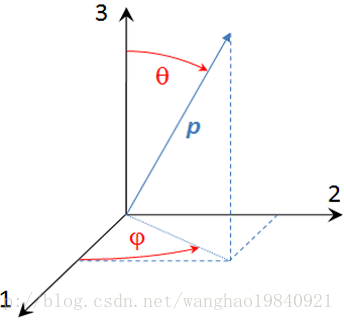
图1.8 单个夹杂体的方向

　　由于RVE中每个夹杂体的轴向量 $\mathbf{p}$均不相同，所以引入 方向分布函数（ODF）$\psi \left( \mathbf{p} \right)$ 。通过定义 $\psi \left( \mathbf{p} \right)d\mathbf{p}$来表示在角 $\left[ {\mathbf{p},\mathbf{p} + d\mathbf{p}} \right]$范围内找寻纤维的概率。
　　考虑一般情况：有 $N$族夹杂增强的复合材料，每个夹杂通过相同的刚度、纵横比和ODF来定义：

• 基体相（域${\omega _0}$）：体分比 ${\nu _0}$，刚度 ${\mathbf{C}_0}$；
  • $N$个夹杂族$(i)$：${\nu _i}$，${\mathbf{C}_i}$，${\rm{A}}{{\rm{R}}_i}$，ODF ${\psi _i}\left( \mathbf{p} \right)$。

  • 显然，基体和所有夹杂族的体分比和为1：
    

    $${\nu _0} + \sum\limits_{i = 1}^N {{\nu _i}} = 1$$
    　　每个ODF遵循两个条件：
    $${\psi _i}\left( \mathbf{ p} \right) = {\psi _i}\left( { - \mathbf{p}} \right),\;\;\;\;\oint {{\psi _i}\left( \mathbf{p} \right)d \mathbf{p} = 1}$$
    其中，第一个方程表示两个相反轴向量为相同的夹杂体；第二个方程是归一化条件，表示概率和为1.
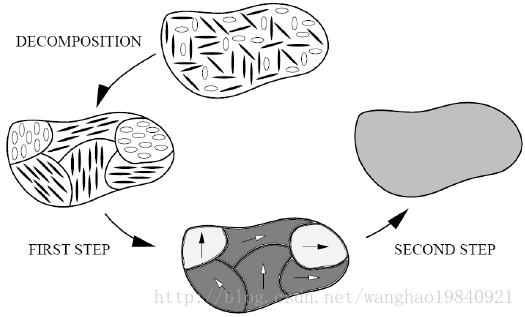
    　　该复合材料在Digimat-MF中分两步进行均匀化，如图1.9所示。真实的RVE被一个伪晶粒的集合来代替。每个伪晶粒占据一个区域 ${\omega _{i,p}}$，是一个基本的两相复合材料，由基体相 ${\nu _0}$和等效对齐的夹杂体集合（该集合从方向 $\left[ {\mathbf{p},\mathbf{p} + d\mathbf{p}} \right]$范围内的夹杂族组合而成）组成 。
    1. 每个伪晶粒通过适用于两相复合材料的MFH模型（如Mori-Tanaka或者interpolative Double inclusion）来进行均匀化；
    2. 计算均匀化后的伪晶粒的有效响应。在当前版本的Digimat-MF中，该步应用的是Voigt模型。尽管Voigt模型不适用于真实的复合材料，但对于本模型，我们的经验表明预测精度较高，即使在最通常的情况下$N = 1$。
       
       
       
       图1.9 适用于无序夹杂复合材料的两步均匀化程序。上：真实RVE。左中：分解为伪晶粒的集合。下：每个伪晶粒的均匀化（第一步）。右中：均匀化伪晶粒集合的均匀化（第二步）
       
    
    【本文译自Digimat-MF帮助文档。】