支持向量机

支持向量机

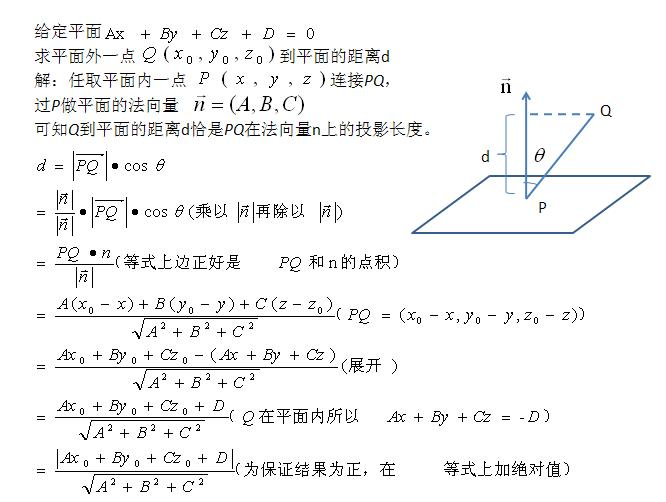
点到平面的距离

平面的一般式方程

$$w_1x_1+w_2x_2+w_3x_3+b=w^Tx+b=0$$
其中 $w = (w_1,w_2,w_3)$ 是平面的法向量， $b$ 是将平面平移到坐标原点所需距离（所以 $b=0$ 时，平面过原点）

向量的模

给定一个向量 $w = (w_1,w_2,w_3)$, 则 $|w| = sqrt(w_1^2+ w_2^2+ w_3 ^2)$

向量的内积

给定两个向量 $w = (w_1,w_2,w_3)$ 和 $x = (x_1,x_2,x_3)$ 则他们的内积是

$$wx = w_1x_1+w_2x_2+w_3x_3$$

点到平面的距离

!

最优间隔分类器与支持向量

函数间隔和几何间隔

令划分超平面的线性方程为

$$w^Tx+b=0$$
假设超平面能正确分类，当 $w^Tx+b>0$ 的点对应 $y=1$ 的数据点， $w^Tx+b<0$ 的点对应 $y=-1$ 的点。
给定一个训练样本 $(x^{(i)},y^{(i)})$。我们定义函数间隔如下：
$${\over{ \gamma}} ^{(i)}= {y^{\left( i \right)}}\left( {{w^T}{x^{\left( i \right)}} + b} \right)$$
实际上
$${\over{ \gamma}} ^{(i)}= {{\left| {{w^T}x^{(i)} + b} \right|}}$$

为了使函数间隔最大（更大的信心确定该例是正例还是反例），当$y^{(i)}=1$ 时，${{w^T}x^{(i)} + b}$ 应该是个大正数，反之是个大负数。因此函数间隔代表了我们认为特征是正例还是反例的确信度。

继续考虑 $w$ 和 $b$，如果同时加大$w$ 和 $b$，比如在 ${{w^T}x^{(i)} + b}$ 前面乘个系数比如2，那么所有点的函数间隔都会增大二倍，这个对求解问题来说不应该有影响，因为我们要求解的是 ${{w^T}x^{(i)} + b}=0$ ，同时扩大 $w$ 和 $b$对结果是无影响的。这样，我们为了限制 $w$ 和 $b$，可能需要加入归一化条件

现在我们定义全局样本上的函数间隔

$${\over{ \gamma}} = \mathop {\min }\limits_{i=1,...,m}{\over{ \gamma}} ^{(i)}$$

说白了就是在训练样本上分类正例和负例确信度最小那个函数间隔。

样本空间任意点 $x^{(i)}$ 到超平面的几何间隔为

$$r^{(i)} = {{\left| {{w^T}x^{(i)} + b} \right|} \over {\left\| w \right\|}}= {{\over{ \gamma}} ^{(i)} \over {\left\| w \right\|}}$$
函数间隔归一化结果就是几何间隔。同时扩大 $w$ 和 $b$， $w$ 扩大几倍，${\left\| w \right\|}$　就扩大几倍，结果无影响。
定义全局的几何间隔
$$r= \mathop {\min }\limits_{i=1,...,m}r^{(i)}$$

分类学习最基本的想法就是基于给定训练集在样本空间中找到一个划分超平面，将不同的类别样本分开。但满足这种要求的划分超平面有很多。
!

如何确定这个超平面

直观上讲，这个超平面应该是最适合分开两类数据的直线。而判定“最适合”的标准就是寻找一个超平面，使得离超平面比较近的点能有更大的间距。也就是我们不考虑所有的点都必须远离超平面，我们关心求得的超平面能够让所有点中离它最近的点具有最大间距。

形式化表示为

$$\mathop {\max }\limits_{r,w,b}{{\over{ \gamma}}\over {\left\| w \right\|}}\\ s.t.{\rm{ }}{y^{(i)}}\left( {{w^T}{x^{(i)}} + b} \right) \ge{\over{ \gamma}} {\rm{, }}i = 1,2,...,m$$

前面说到同时扩大 $w$ 和 $b$ 对结果没有影响，但我们最后要求的仍然是 $w$ 和 $b$ 的确定值。因此，我们需要对 $\over \gamma$ 做一些限制，以保证我们解是唯一的。这里为了简便我们取 ${\over{ \gamma}} =1$ 。这样的意义是将全局的函数间隔定义为1。即将离超平面最近的点的距离定义为$1\over {\left\| w \right\|}$
即令

$$\left\{ \matrix{ {w^T}{x_i} + b \ge + 1{\rm{,}}{{\rm{y}}_i} = + 1\cr {w^T}{x_i} + b \le - 1{\rm{,}}{{\rm{y}}_i} = - 1 \cr} \right.$$
如下图所示

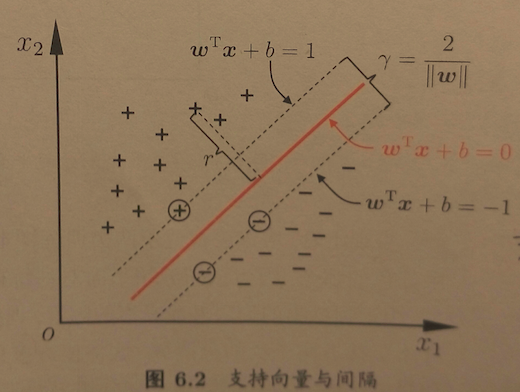
上式使得等号成立的几个样本点被称为支持向量

两个异类支持向量到超平面距离之和为：

$$\gamma = {2 \over {\left\| w \right\|}}$$
被称为 间隔

最大间隔划分超平面

欲找到最大间隔的划分超平面，我们得到改写后的目标函数为

$$\eqalign{ & \mathop {\max }\limits_{w,b} {2 \over {\left\| w \right\|}} \cr & s.t.{\rm{ }}{y_i}\left( {{w^T}{x_i} + b} \right) \ge 1{\rm{, }}i = 1,2,...,m \cr}$$

我们在优化时喜欢求最小值，将上式转化正等价的求最小值如下

$$\eqalign{ & \mathop {\min }\limits_{w,b} {1 \over 2}{\left\| w \right\|^2} \cr & s.t.{\rm{ }}{y_i}\left( {{w^T}{x_i} + b} \right) \ge 1{\rm{, }}i = 1,2,...,m \cr}$$
这就是支持向量机的 基本型

对偶问题

对偶问题转化

上式是一个凸二次规划问题，我们可以使用拉格朗日乘数法进行优化，对每个约束添加拉格朗日乘子 $\alpha_i \ge 0$。则问题的拉格朗日函数可写为

$$L(w,b,\alpha ) = {1 \over 2}{\left\| w \right\|^2} + \sum\limits_{i = 1}^m {{\alpha _i}\left( {1 - {y_i}\left( {{w^T}{x_i} + b} \right)} \right)}$$
式中 $\alpha_i$是拉格朗日乘子.
我们令
$$\theta (w) = \mathop {\max }\limits_{{\alpha _i} \ge 0} L(w,b,\alpha )$$
如果约束条件都满足， $\theta (w)$ 的最优值就是 ${1 \over 2}{\left\| w \right\|^2}$，和目标函数一样。

因此我们可以直接求 $\theta (w)$ 的最小值，等价于求原目标函数。因此目标函数变成如下

$$\mathop {\min }\limits_{w,b} \theta (w) = \mathop {\min }\limits_{w,b} \mathop {\max }\limits_{{\alpha _i} \ge 0} L(w,b,\alpha )=p^*$$

将求最大值和最小值交换位置，得到原始问题的对偶问题

$$\mathop {\max }\limits_{{\alpha _i} \ge 0} \mathop {\min }\limits_{w,b} L(w,b,\alpha ) = {d^*}$$

满足

$$d^* \le p^*$$
在满足某些条件的情况下(满足KKT条件)，这两者相等，这个时候就可以通过求解对偶问题来间接地求解原始问题。

对偶问题求解

分别求 $L$ 对 $w,b$ 的导数，并令其为0，得如下结果

$$\eqalign{ & {{\partial L} \over {\partial w}} = 0 \Rightarrow w = \sum\limits_{i = 1}^m {{\alpha _i}{y_i}{x_i}} \cr & {{\partial L} \over {\partial b}} = 0 \Rightarrow \sum\limits_{i = 1}^m {{\alpha _i}{y_i}} = 0 \cr}$$

带入 $L(w,b,\alpha )$ 得到 $\mathop {\min }\limits_{w,b} L(w,b,\alpha )$

$$\eqalign{ & \mathop {\min }\limits_{w,b} L(w,b,\alpha ) = {1 \over 2}\sum\limits_{i,j = 1}^m {{\alpha _i}{\alpha _j}{y_i}{y_j}x_i^T{x_j} - } \sum\limits_{i,j = 1}^m {{\alpha _i}{\alpha _j}{y_i}{y_j}x_i^T{x_j}} \cr & - b\sum\limits_{i = 1}^m {{\alpha _i}{y_i}} + \sum\limits_{i = 1}^m {{\alpha _i}} = \sum\limits_{i = 1}^m {{\alpha _i}} - {1 \over 2}\sum\limits_{i,j = 1}^m {{\alpha _i}{\alpha _j}{y_i}{y_j}x_i^T{x_j}} \cr}$$

然后求最大值，从上面的式子得到对偶问题

$$\eqalign{ & \mathop {\max }\limits_{{\alpha _i} \ge 0} \sum\limits_{i = 1}^m {{\alpha _i}} - {1 \over 2}\sum\limits_{i,j = 1}^m {{\alpha _i}{\alpha _j}{y_i}{y_j}x_i^T{x_j}} \cr & s.t.{\rm{ }}\sum\limits_{i = 1}^m {{\alpha _i}} {y_i} = 0{\rm{, }}{\alpha _i} \ge 0{\rm{, }}i = 1,2,...,m \cr}$$

上式是关于 $\alpha$ 的式子，如果能求出 $\alpha$ ，则通过 $w = \sum\limits_{i = 1}^m {{\alpha _i}{y_i}{x_i}}$ 可以求出 $w$，再根据前面函数距离等于1的假设求出 $b$。

得到模型

$$f\left( x \right) = {w^T}x + b = \sum\limits_{i = 1}^m {{\alpha _i}{y_i}x_i^Tx} + b = \sum\limits_{i = 1}^m {{\alpha _i}{y_i}} \left\langle {{x_i},x} \right\rangle + b$$
对于新点 $x$ 的预测，只需计算它与训练数据点的内积即可。且所有非支持向量所对应的系数 $α$ 都等于零(这里为满足 $\mathop {\max }\limits_{{\alpha _i} \ge 0} L(w,b,\alpha )$ 最大化必须等于0)，因此对于内积计算只针对支持向量即可。

拉格朗日乘子法和KKT条件

拉格朗日乘子法和KKT(Karush-Kuhn-Tucker)条件是求解约束优化问题的重要方法，在有等式约束时使用拉格朗日乘子法，在有不等约束时使用KKT条件。

前提：只有当目标函数为凸函数时，使用这两种方法才保证求得的是最优解。

最优化问题分类:
1). 如果目标函数和约束条件都为变量的线性函数, 称该最优化问题为线性规划;
2). 如果目标函数为变量的二次函数, 约束条件为变量的线性函数, 称该最优化问题为二次规划;
3). 如果目标函数或者约束条件为变量的非线性函数, 称该最优化问题为非线性规划.

拉格朗日乘子法–等式约束问题

对于等式约束问题

$$\mathbf{x^\star} = \underset{\mathbf{x}}{\textrm{argmin}} f(\mathbf{x}) \\\textrm{subject to } h_i(\mathbf{x}) = 0, \forall i=1,..,m$$
利用拉格朗日乘子法，原问题转换为
$$\mathbf{x^\star} = \underset{\mathbf{x}}{\textrm{argmin }} L(\mathbf{x}, \mathbf{\lambda}) = \underset{\mathbf{x}}{\textrm{argmin }} f(\mathbf{x}) + \underset{i=1}{\overset{m}{\sum}} \lambda_i h_i(\mathbf{x}),$$
其中 $\lambda_{i}\ne{0}$，称为拉格朗日乘子，这样我们有了 $k+m$ 个变量。

通过对 $x$ 求偏导，找最优解，得到最优的条件

$$\nabla_{\mathbf{x}}L(\mathbf{x}, \lambda) = \nabla_{\mathbf{x}}f(\mathbf{x}) + \sum_i\lambda_i \nabla_{\mathbf{x}}h_i(\mathbf{x}) = 0$$

我们得到了 $k$ 个方程式。进一步对拉格朗日乘子求偏导，得到另外 $m$ 个方程式

$$\frac{\partial L(\mathbf{x}, \lambda)}{\partial \lambda_i} = h_i(\mathbf{x}) = 0,$$

这里通过强制偏导数为零，我们同样可以限制可能的解满足原始约束条件。现在变量数与方程数相同，使得方程解唯一。

等式约束问题的合理性

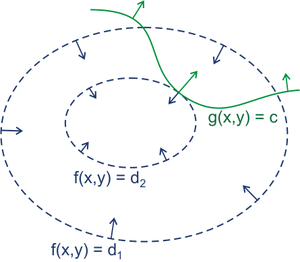
举个二维最优化的例子

$$\min\;f(x,y)\\s.t.\;g(x,y)=c$$

我们可以画图来辅助思考
!Alt text

蓝线是 $f(x,y)$ 的等高线。箭头表示斜率，和等高线的法线平行。从梯度的方向上来看，显然有 $d_1>d_2$。
绿线标出的是约束 $g(x,y)=c$ 的点的轨迹，也就是说，只要正好落在这条绿线上的点才可能是满足要求的点。

最小值点应该在哪里呢？显然应该是在 $f(x,y)$ 的等高线正好和约束线相切的位置，因为如果只是相交意味着肯定还存在其它的等高线在该条等高线的内部或者外部，使得新的等高线与目标函数的交点的值更大或者更小，只有到等高线与目标函数的曲线相切的时候，可能取得最优值。

很容易看出来，要想让目标函数 $f(x,y)$ 的等高线和约束相切，则他们切点的梯度一定在一条直线上。即在最优解处，$f$ 和 $g$ 的斜率平行。
因此，我们通过观察可以得到优化取到最小值时满足

$$\bigtriangledown[f(x,y)+\lambda(g(x,y)-c)]=0\;\;\;\;\lambda\ne{0}$$

这个结果正好等价于方程 $F(x,y)=f(x,y)+\lambda(g(x,y)-c)$ 对 $x$ 求偏导。方程 $F(x,y)$ 在达到极值时与 $f(x,y)$ 相等，因为$F(x,y)$达到极值时$g(x,y)−c$总等于零。

拉格朗日乘子法–不等式约束问题

当同时存在不等式约束时，新的问题描述为

$${x^*} = \underset{{x}}{\textrm{argmin}} f({x})$$
$$\textrm{subject to } h_i({x}) = 0, \forall i=1,..,m \\\textrm{subject to } g_i({x}) \le 0, \forall i=1,..,n$$

此时不等式约束下的最优化问题描述为

$${x^*} = \underset{{x}}{\textrm{argmin }} L({x}, {\lambda}, {\mu}) = \underset{{x}}{\textrm{argmin }} f({x}) + \underset{i=1}{\overset{m}{\sum}} \lambda_i h_i({x}) + \underset{i=1}{\overset{n}{\sum}} \mu_i g_i({x})$$

其中 $L({x}, {\lambda}, {\mu})$ 为拉格朗日函数，$\lambda_i$ 对应等式约束系数，$\mu_{k}$ 对应不等式约束系数。现在总共有 $k+m+n$个变量。

跟等式约束一样，我们想通过对 $x$ 与 $\lambda$ 求偏导，得到 $k+m$ 个方程式。接下来的问题是怎么通过不等式约束得到更多的 $n$ 个方程式。

对于不等式约束，当极值点存在 $g_i({x^*}) \lt 0$ 区域，那么这个约束不影响极值的取值，等同于没有约束。因此它的系数 $\mu_i$ 可以设置为0。另一方面，如果极值在约束边界上，此时，$g_i({x^*}) = 0$。如下图所示

综合可得到

$$\mu_i g_i({x}) = 0$$
为问题的必要条件。至此，我们得到了 $n$ 个方程式通过不等式约束。系数 $\lambda_i$ 可以为任意值，没有符号的限制。然而 $\mu_{k} \ge 0$ ，下图解释说明。

假设 $x^*$ 在 $g_i({x})=0$ 区域内，那么 $\mu_{i}$ 可以不为零。

$${x^*} = \underset{{x}}{\textrm{argmin }} f({x}) + \mu_i g_i({x}) \\0 = \nabla f({x}) + \mu_i \nabla g_i({x}) \\\begin{equation}\mu_i = -\frac{\nabla f({x})}{\nabla g_i({x})}\label{eq:signofmu}\end{equation}$$

在 $x^*$ 点处，$f(x)$ 与 $g_i(x)$ 的梯度方向像相反。所以 $\mu_{i} \ge 0$

KKT条件

对于一个标准形式的最优化数学模型

$${x^*} = \underset{{x}}{\textrm{argmin}} f({x})$$
$$\textrm{subject to } h_i({x}) = 0, \forall i=1,..,m \\\textrm{subject to } g_i({x}) \le 0, \forall i=1,..,n$$
KKT条件是一个非线性规划问题能有最优化解法的必要和充分条件。KKT条件就是指上面最优化问题中的最小点 $x^*$ 必须满足下面的条件：
$$\left\{\matrix{ Stationarity: \\& 0 = \nabla f({x}) + \sum_i\lambda_i \nabla_{}h_i(\mathbf{x}) + \sum_i{\mu_i \nabla g_i({x}) }\\ Primal feasibility:\\& h_i({x}) = 0, \forall i=1,..,m\\& g_i({x}) \le 0, \forall i=1,..,n\\ Dual feasibility:\\& \mu_{i}\ge{0}, \forall i=1,..,n\\ Complementary slackness:\\& \mu_i g_i({x}) = 0, \forall i=1,..,m } \right.$$

不等式约束问题的合理性

为什么可对偶问题求解

$$\left.\begin{matrix}L(x,\mu)=f(x)+\sum_{k=1}^q\mu_{k}g_{k}(x)\\\mu_{k}\ge{0}\\g_{k}(x)\le{0}\end{matrix}\right\}$$

$$\because \left.\begin{matrix}\mu_{k}\ge{0}\\g_{k}(x)\le{0}\end{matrix}\right\}=> \mu{g(x)}\le{0}$$
$$\therefore \begin{equation}\max_{\mu}L(x,\mu)=f(x)\label{a}\end{equation}$$
$$\therefore\begin{equation}\min_{x}f(x)=\min_{x}\max_{\mu}L(x,\mu)\label{firsthalf}\end{equation}$$
$$\max_{\mu}\min_{x}L(x,\mu)=\max_{\mu}[\min_{x}f(x)+\min_{x}\mu{g(x)}]=\\\max_{\mu}\min_{x}f(x)+\max_{\mu}\min_{x}\mu{g(x)}=\min_{x}f(x)+\max_{\mu}\min_{x}\mu{g(x)}$$
$$\because\left.\begin{matrix}\mu_{k}\ge{0}\\g_{k}(x)\le{0}\end{matrix}\right\}=>\min_{x}\mu{g(x)}=\left\{\begin{matrix}0 & if\;\mu=0\;or\;g(x)=0\\ -\infty & if\;\mu>0\;and\;g(x)<0\end{matrix}\right.$$
$$\therefore \max_{\mu}\min_{x}\mu{g(x)}=0$$
此时 $\mu=0\;or\;g(x)=0$
$$\begin{equation}\therefore \max_{\mu}\min_{x}L(x,\mu)=\min_{x}f(x)+\max_{\mu}\min_{x}\mu{g(x)}=\min_{x}f(x)\label{secondhalf}\end{equation}$$
此时 $\mu=0\;or\;g(x)=0$
联合 $\eqref{firsthalf}, \eqref{secondhalf}$我们得到 > $$\min_{x}\max_{\mu}L(x,\mu)=\max_{\mu}\min_{x}L(x,\mu)$$
即 $$\left.\begin{matrix}L(x,\mu)=f(x)+\sum_{k=1}^q\mu_{k}g_{k}(x)\\\mu_{k}\ge{0}\\g_{k}(x)\le{0}\end{matrix}\right\}$$ => $$\min_{x}\max_{\mu}L(x,\mu)=\max_{\mu}\min_{x}L(x,\mu)=\min_{x}f(x)$$

我们把 $\max_{\mu}\min_{x}L(x,\mu)$ 称为原问题 $\min_{x}\max_{\mu}L(x,\mu)$ 的对偶问题，上式表明当满足一定条件时原问题、对偶的解、以及 $\min_{x}f(x)$ 是相同的，且在最优解 $x^∗$ 处$\mu=0\;or\;g(x^*)=0$。把 $x^∗$ 代入 $\eqref{a}$ 得 $\max_{\mu}L(x^*,\mu)=f(x^*)$ ，由 $\eqref{secondhalf}$ 得 $\max_{\mu}\min_{x}L(x,\mu)=f(x^*)$ ，所以 $L(x^*,\mu)=\min_{x}L(x,\mu)$ ，这说明 $x^∗$ 也是 $L(x,μ)$ 的极值点，即 $\frac{\partial{L(x,\mu)}}{\partial{x}}|_{x=x^*}=0$。

最后总结一下：

$$\left.\begin{matrix}L(x,\mu)=f(x)+\sum_{k=1}^q\mu_{k}g_{k}(x)\\\mu_{k}\ge{0}\\g_{k}(x)\le{0}\end{matrix}\right\}$$ => $$\left\{\begin{matrix}\min_{x}\max_{\mu}L(x,\mu)=\max_{\mu}\min_{x}L(x,\mu)=\min_{x}f(x)=f(x^*)\\\mu_{k}{g_{k}(x^*)=0}\\\frac{\partial{L(x,\mu)}}{\partial{x}}|_{x=x^*}=0\end{matrix}\right.$$

KKT条件是拉格朗日乘子法的泛化，如果我们把等式约束和不等式约束一并纳入进来则表现为：

$$\left.\begin{matrix}L(x,\lambda,\mu)=f(x)+\sum_{i=1}^{n}\lambda_{i}h_{i}(x)+\sum_{k=1}^q\mu_{k}g_{k}(x)\\\lambda_{i}\ne{0}\\h_{i}(x)=0\\\mu_{k}\ge{0}\\g_{k}(x)\le{0}\end{matrix}\right\}$$
=>
$$\left\{\begin{matrix}\min_{x}\max_{\mu}L(x,\lambda,\mu)=\max_{\mu}\min_{x}L(x,\lambda,\mu)=\min_{x}f(x)=f(x^*)\\\mu_{k}{g_{k}(x^*)=0}\\\frac{\partial{L(x,\lambda,\mu)}}{\partial{x}}|_{x=x^*}=0\end{matrix}\right.$$

$\frac{\partial{L(x,\lambda,\mu)}}{\partial{x}}|_{x=x^*}=0$ 表明$f(x)$在极值点$x^∗$ 处的梯度是各个 $h_i(x^∗)$ 和 $g_k(x^∗)$ 梯度的线性组合。

核函数

支持向量机是建立在统计学习理论基础之上的新一代机器学习算法，支持向量机的优势主要体现在解决线性不可分问题，它通过引入核函数，巧妙地解决了在高维空间中的内积运算，从而很好地解决了非线性分类问题。

特征空间的隐式映射

前面的讨论中，我们假设训练样本是线性可分的，即存在一个划分超平面能将训练样本正确分类。事实上大部分时候数据并不是线性可分的，这个时候满足这样条件的超平面就根本不存在。

对于非线性的情况，SVM 的处理方法是选择一个核函数 $κ(⋅,⋅)$ ，通过将数据从原始空间映射到一个更高维的特征空间，使得样本在特征空间内线性可分，来解决在原始空间中线性不可分的问题。

具体来说，在线性不可分的情况下，支持向量机首先在低维空间中完成计算，然后通过核函数将输入空间映射到高维特征空间，最终在高维特征空间中构造出最优分离超平面，从而把平面上本身不好分的非线性数据分开。

令 $\phi \left( x \right)$ 表示将 $x$ 映射后的特征向量，于是，在特征空间中的划分超平面所对应的模型可表示为

$$f\left( x \right) = {w^T}\phi \left( x \right) + b$$
这意味着建立非线性学习器分为两步：首先使用一个非线性映射将数据变换到一个特征空间。然后在特征空间使用线性学习器分类

类似于原始空间线性可分的问题，可以得到特征空间的SVM基本型

$$\eqalign{ & \mathop {\min }\limits_{w,b} {1 \over 2}{\left\| w \right\|^2} \cr & s.t.{\rm{ }}{y_i}\left( {{w^T}\phi \left( x_i \right) + b} \right) \ge 1{\rm{, }}i = 1,2,...,m \cr}$$

其对偶问题是

$$\eqalign{ & \mathop {\max }\limits_{{\alpha _i} \ge 0} \sum\limits_{i = 1}^m {{\alpha _i}} - {1 \over 2}\sum\limits_{i,j = 1}^m {{\alpha _i}{\alpha _j}{y_i}{y_j}\phi \left( x_i \right)^T{\phi \left( x_j \right)}} \cr & s.t.{\rm{ }}\sum\limits_{i = 1}^m {{\alpha _i}} {y_i} = 0{\rm{, }}{\alpha _i} \ge 0{\rm{, }}i = 1,2,...,m \cr}$$

求解上式涉及到计算 $\phi \left( x_i \right)^T{\phi \left( x_j \right)}$，这是样本在特征空间的内积。

求 $\phi \left( x_i \right)^T{\phi \left( x_j \right)}$ 可以有两种方法
1、先找到这种映射，然后将输入空间中的样本映射到新的空间中，最后在新空间中去求内积
2、或者是找到某种方法，它不需要显式的将输入空间中的样本映射到新的空间中，而能够在输入空间中直接计算出内积，这就是传说中的核函数方法

由于特征空间维数可能很高，直接计算通常困难。为了避开障碍，可以设想一个这样的函数

$$k\left( {{x_i},{x_j}} \right) = \left\langle {\phi \left( {{x_i}} \right),\phi \left( {{x_j}} \right)} \right\rangle = \phi {\left( {{x_i}} \right)^T}\phi \left( {{x_j}} \right)$$

即特征空间的内积等于在原始空间中通过函数 $k(.,.)$ 计算而得。这样就不必直接去计算高维特征空间的内积。于是上式可重写为

$$\eqalign{ & \mathop {\max }\limits_{{\alpha _i} \ge 0} \sum\limits_{i = 1}^m {{\alpha _i}} - {1 \over 2}\sum\limits_{i,j = 1}^m {{\alpha _i}{\alpha _j}{y_i}{y_j}k\left( {{x_i},{x_j}} \right) } \cr & s.t.{\rm{ }}\sum\limits_{i = 1}^m {{\alpha _i}} {y_i} = 0{\rm{, }}{\alpha _i} \ge 0{\rm{, }}i = 1,2,...,m \cr}$$

求解后可得到

$$f\left( x \right) = {w^T}\phi \left( x \right) + b = \sum\limits_{i = 1}^m {{\alpha _i}{y_i}\phi {\left( {{x_i}} \right)^T}\phi \left( {{x}} \right)} + b = \sum\limits_{i = 1}^m {{\alpha _i}{y_i}}k\left( {{x_i},{x}} \right) + b$$

这里的函数 $k\left( .,. \right)$ 就是核函数。

定义：核是一个函数 $K$，对于所有的 $x_1,x_2 \in X$ 满足，$K<x_1,x_2>=<\Phi(x_1),\Phi(x_2)>$，这里的 $\Phi$ 为从 $X$ 到内积特征空间 $F$ 的映射。

核函数有效性判定

先看一个例子，假设 $x$ 和 $z$ 都是 $n$维的 $K(x,z)=(x^Tz)^2$ 展开后，得

$$k\left( {x,z} \right) = {\left( {{x^T}z} \right)^2} = \left( {\sum\limits_{i = 1}^n {{x_i}{z_i}} } \right)\left( {\sum\limits_{j = 1}^n {{x_j}{z_j}} } \right) = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\left( {{x_i}{x_j}} \right)\left( {{z_i}{z_j}} \right)} } = \phi {\left( x \right)^T}\phi \left( z \right)$$
现在看一下映射函数（n=3时），根据上面的公式，得到
$$\phi \left( x \right) = {\left[ {\matrix{ {{x_1}{x_1}} & {{x_1}{x_2}} & {{x_1}{x_3}} & {{x_2}{x_1}} & {{x_2}{x_2}} & {{x_2}{x_3}} & {{x_3}{x_1}} & {{x_3}{x_2}} & {{x_3}{x_3}} \cr } } \right]^T}$$

这个时候发现我们可以只计算原始特征 $x$ 和 $z$ 内积的平方，就等价与计算映射后特征的内积。也就是说核函数 $K(x,z)=(x^Tz)^2$ 只能在选择这样的 $\phi$ 作为映射函数时才能够等价于映射后特征的内积。

我们再看一个核函数

$$k\left( {x,z} \right) = {\left( {{x^T}z + c} \right)^2} = \left( {\sum\limits_{i = 1}^n {{x_i}{z_i}} + c} \right)\left( {\sum\limits_{j = 1}^n {{x_j}{z_j}} + c} \right) \\= \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\left( {{x_i}{x_j}} \right)\left( {{z_i}{z_j}} \right)} } + \left( {\sum\limits_{i = 1}^n {\left( {\sqrt {2c} {x_i}} \right)\left( {\sqrt {2c} {z_i}} \right)} } \right) + {c^2}$$

对应的映射函数（n=3时）是

$$\phi \left( x \right) = {\left[ {\matrix{ {{x_1}{x_1}} & {{x_1}{x_2}} & {{x_1}{x_3}} & {{x_2}{x_1}} & {{x_2}{x_2}} & {{x_2}{x_3}} & {{x_3}{x_1}} & {{x_3}{x_2}} & {{x_3}{x_3}} \cr } \matrix{ {\sqrt {2c} {x_1}} & {\sqrt {2c} {x_2}} & {\sqrt {2c} {x_3}} & c \cr } } \right]^T}$$

半正定矩阵

实对称矩阵：如果有 $n$ 阶矩阵 $A$，其各个元素都为实数，矩阵A的转置等于其本身，则称 $A$ 为实对称矩阵。
主要性质
1.实对称矩阵 $A$ 的不同特征值对应的特征向量是正交的。
2.实对称矩阵 $A$ 的特征值都是实数，特征向量都是实向量。
3.$n$ 阶实对称矩阵 $A$ 必可对角化，且相似对角阵上的元素即为矩阵本身特征值。

埃尔米特矩阵：$n$ 阶复方阵 $A$ 的对称单元互为共轭，即 $A$ 的共轭转置矩阵等于它本身，则 $A$ 是埃尔米特矩阵。显然它是实对称阵的推广。

半正定矩阵：一个 $n× n$ 的埃尔米特矩阵 $M$ 是正定的当且仅当对于每个非零的复向量 $z$，都有 $z^*Mz > 0$，则称$M$ 为正定矩阵，其中$z^*$ 表示$z$ 的共轭转置。当$z^*Mz > 0$弱化为 $z^*Mz≥0$ 时，称 $M$ 是半正定矩阵。
判定：所有主子式大于或等于零

问题描述与分析

给定一个函数 $K$，我们能否使用 $K$ 来替代计算 $\phi {\left( {{x}} \right)^T}\phi \left( {{z}} \right)$，也就说，是否能够找出一个 $\phi$，使得对于所有的 $x$ 和 $z$，都有 $k\left( {x,z} \right) = \phi {\left( {{x}} \right)^T}\phi \left( {{z}} \right)$。 比如给出了 $k\left( {x,z} \right) = (x^Tz)^2$，是否能够认为 $K$ 是一个有效的核函数。

下面来解决这个问题，给定 $m$ 个训练样本 $\{{x^{(1)},x^{(2)},...,x^{(m)}}\}$，每一个 $x^{(i)}$ 对应一个特征向量。那么，我们可以将任意两个 $x^{(i)}$ 和 $x^{(j)}$ 带入 $K$ 中，计算得到 $K_{ij}=K(x^{(i)},x^{(j)})$。$i$ 可以从1到 $m$，$j$ 可以从1到 $m$，这样可以计算出 $m*m$ 的核函数矩阵。我们用 $K$ 来表示。

有效地核函数定义

如果假设 $K$ 是有效地核函数，那么根据核函数定义

$${K_{ij}} = K\left( {{x^{\left( i \right)}},{x^{\left( j \right)}}} \right) = \phi {\left( {{x_i}} \right)^T}\phi \left( {{x_j}} \right) = \phi {\left( {{x_j}} \right)^T}\phi \left( {{x_i}} \right) = K\left( {{x^{\left( j \right)}},{x^{\left( i \right)}}} \right) = {K_{ji}}$$

可见，矩阵K应该是个对称阵。
再者，对于任意向量 $z$，得

$$\eqalign{ & {z^T}Kz = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\left( {{z_i}{K_{ij}}{z_j}} \right)} } = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\left( {{z_i}\phi {{\left( {{x_i}} \right)}^T}\phi \left( {{x_j}} \right){z_j}} \right)} } = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\left( {{z_i}\sum\limits_{k = 1}^n {{\phi _k}\left( {{x_i}} \right){\phi _k}\left( {{x_j}} \right){z_j}} } \right)} } \cr & = \sum\limits_{k = 1}^n {\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{z_i}{\phi _k}\left( {{x_i}} \right){\phi _k}\left( {{x_j}} \right){z_j}} } } = {\sum\limits_{k = 1}^n {\left( {{z_i}{\phi _k}\left( {{x_i}} \right)} \right)} ^2} \ge 0 \cr}$$

从这个公式我们可以看出，如果 $K$ 是个有效的核函数，那么在训练集上得到的核函数矩阵 $K$ 应该是半正定的。这样我们得到一个核函数的必要条件：K是有效的核函数 => 核函数矩阵K是对称半正定的。

可幸的是，这个条件也是充分的，由Mercer定理来表达。Mercer定理表明为了证明 $K$ 是有效的核函数，那么我们不用去寻找 $\phi$，而只需要在训练集上求出各个 $K_{ij}$，然后判断矩阵 $K$ 是否是半正定（使用左上角主子式大于等于零等方法）即可。

假设有输入空间 $X=x_1,x_2,...,x_n$ 且 $K(x,u)$ 为对称函数，那么对于所有样本得到矩阵 $k=(K(x_i,x_j)),(i,j=0,...,n)$，显然这是对称阵，那么存在一个正交矩阵 $P$ ，使得 $P^TkP=\Lambda$，这里 $\Lambda$是包含 $k$ 的特征值 $\lambda$ 的对角阵，特征值 $\lambda$ 对应的特征向量为 $v_i=(v_{1i},v_{2i},...,v_{ni})^T$，对输入空间做如下映射 $\phi$:

$$\eqalign{ & \phi \left( {{x_i}} \right) = \left( {\matrix{ {\sqrt {{\lambda _1}} {v_{1i}}} & {\sqrt {{\lambda _2}} {v_{2i}}} & \cdots & {\sqrt {{\lambda _n}} {v_{ni}}} \cr } } \right) \cr}$$

于是有

$$\left\langle {\phi \left( {{x_i}} \right),\phi \left( {{x_j}} \right)} \right\rangle = \sum\limits_{t = 1}^n {{\lambda _t}{v_{ti}}} {v_{tj}} = {\left( {V\Lambda {V^T}} \right)_{i,j}} = {k_{ij}}$$

(其中 $V$ 为特征向量组成的矩阵，$\Lambda$ 为相应特征值组成的三角矩阵)，也就是说 $K$ 是对应于映射 $\phi$ 的核函数。

例子：有 $k=\left[\begin{array}{cccc} 4&0&0\\ 0&3&1\\ 0&1&3\ \end{array}\right]$
由 $|k-\lambda E|=0$ 解得特征值：$\lambda_1=\lambda_2=4，\lambda_3=2$

对2重特征根4求 $(A-4E)x=0$ 的基础解系、正交化、单位化后得到特征向量：

$$v_1=(1,0,0)^T , v_2=(0,\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})^T$$

对 $\lambda_3$ 的特征向量单位化后得到 $v_3=(0,-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})^T$ ，于是有

$$V=(v_1,v_2,v_3)= \left[ \begin{array}{cccc} 1&0&0\\ 0&\frac{1}{\sqrt(2)}&-\frac{1}{\sqrt(2)}\\ 0&\frac{1}{\sqrt(2)}&\frac{1}{\sqrt(2)}\\ \end{array}\right ]$$

满足

$$V^{-1}kV=\Lambda=\left[ \begin{array}{cccc} 4&0&0\\ 0&4&0\\ 0&0&2\\ \end{array}\right ]$$
对所有输入样本做映射得：

$$\phi(x_1)=(\sqrt{4}*1,\sqrt{4}*0,\sqrt{2}*0)=(2,0,0)^T$$
$$\phi(x_2)=(\sqrt{4}*0,\sqrt{4}*\frac{1}{\sqrt{2}},\sqrt{2}*(-\frac{1}{\sqrt{2}}))^T=(0,\sqrt{2},-1)$$
$$\phi(x_3)=(\sqrt{4}*0,\sqrt{4}*\frac{1}{\sqrt{2}},\sqrt{2}*\frac{1}{\sqrt{2}})^T=(0,\sqrt{2},1)$$

随便选两个做内积，如 <ϕ(x2),ϕ(x3)>=0∗0+2√∗2√+(−1)∗1=1=k(x2,x3) <script type="math/tex" id="MathJax-Element-740"><\phi(x_2),\phi(x_3)>=0*0+\sqrt{2}*\sqrt{2}+(-1)*1=1=k(x_2,x_3)</script>。
由此可见：$K(x,y)$ 就是对应于特征映射 $\phi$ 的核函数

定理1：存在有限输入空间 $X，K(x,y)$ 为 $X$ 上的对称函数，那么 $K(x,y)$ 是核函数的充要条件是矩阵 $k=(K(x_i,x_j))\quad\quad(i,j=0,...n)$ 半正定，此时相当于对输入空间向特征空间进行了隐式的$\phi$ 映射。对于上面的映射 $\phi$，令 $\phi_i(x_j)=\sqrt{\lambda_i}v_{ij}$，于是 $\phi(x)=(\phi_1(x),\phi_2(x),...\phi_n(x))$，进而 $K(x,y)=\sum\limits_{i=1}^\infty{\lambda_i\phi_i(x)\phi_i(y)}$。

软间隔与正则化

在前面讨论中，我们假定训练样本在样本空间或特征空间是线性可分的，即可以找到一个可行的超平面将不同类的样本完全分开。然而，现实任务中往往很难确定合适的核函数使得训练样本在特征空间中线性可分。

例如可能并不是因为数据本身是非线性结构的，而只是因为数据有噪音。对于这种偏离正常位置很远的数据点，我们称之为 outlier 。

缓解该问题的一个办法是允许支持向量在一些样本上出错。具体来说，前面介绍的支持向量机形式是要求所有样本均满足约束，即都划分正确，现在考虑到outlier问题，约束条件变成了

$${y_i}\left( {{w^T}\phi \left( x_i \right) + b} \right) \ge 1-{\xi _i} {\rm{, }}i = 1,2,...,m$$

其中 ${\xi _i}$ 称为松弛变量，对应数据点 $x_i$ 不满足约束的程度。当然，如果我们允许 $\xi_i$ 任意大的话，那任意的超平面都是符合条件的了。所以，我们在原来的目标函数后面加上一项，使得这些 $\xi_i$ 的总和也要最小,即不满足约束的样本应尽可能少：

$$\mathop {\min }\limits_{w,b} {1 \over 2}{\left\| w \right\|^2}+C\sum\limits_{i = 1}^m {{\xi _i}}$$

完整地写出来是

$$\mathop {\min }\limits_{w,b} {1 \over 2}{\left\| w \right\|^2}+C\sum\limits_{i = 1}^m {{\xi _i}} \\ s.t., {y_i}\left( {{w^T}\phi \left( x_i \right) + b} \right) \ge 1-{\xi _i} {\rm{, }}i = 1,2,...,m \\ {\xi _i}\ge 0 {\rm{, }}i = 1,2,...,m$$
显然，当 $C$ 为无穷大时，迫使所有样本均满足约束，等价于原问题。

将约束条件加入目标函数中，得到拉格朗日函数

$$L\left( {w,b,\xi ,\alpha ,\mu } \right) = {1 \over 2}{\left\| w \right\|^2} + C\sum\limits_{i = 1}^m {{\xi _i}} + \sum\limits_{i = 1}^m {{\alpha _i}\left( {1 - {\xi _i} - {y_i}\left( {{w^T}{x_i} + b} \right)} \right)} - \sum\limits_{i = 1}^m {{\mu _i}{\xi _i}}$$
$L\left( {w,b,\xi ,\alpha ,\mu } \right)$ 对 $w,b,\xi_i$ 的偏导为零可得到
$$\eqalign{ & w = \sum\limits_{i = 1}^m {{\alpha _i}{y_i}{x_i}} \cr & 0 = \sum\limits_{i = 1}^m {{\alpha _i}{y_i}} \cr & C = {\alpha _i} + {\mu _i} \cr}$$

由 $C = {\alpha _i} + {\mu _i} , {\mu _i} \ge 0$,因此有 $0\le {\alpha _i} \le C$。将 $w$ 带回 $L$ 并化简，并得到目标函数

$$\eqalign{ & \max \sum\limits_{i = 1}^m {{\alpha _i}} - {1 \over 2}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {{\alpha _i}{\alpha _j}{y_i}{y_j}x_i^T} {x_j}} \cr & s.t.\sum\limits_{i = 1}^m {{\alpha _i}{y_i}} = 0,0 \le {\alpha _i} \le C,i = 1,2,...,m \cr}$$
可以看到唯一的区别就是现在 $\alpha$ 多了一个上限 $C$。这样一来，一个可处理线性和非线性并能容忍噪音和 outliers 的支持向量机终于介绍完。

SMO算法详解

SMO算法把整个二次规划问题分解为很多易于处理的小问题，对SVM来说，一次至少要同时对两个样本的Lagrange乘子进行优化，因为等式约束的存在使得我们不可能单独优化一个变量。

当然，这样一次最小优化不可能保证其结果就是最终结果，但会使目标函数向极小值迈进一步。我们再对其它Lagrange乘子做最小优化，直到所有乘子都符合KKT条件时，目标函数达到最小，算法结束。

SMO算法要解决两个问题：一是怎样解决两个变量的优化问题，二是怎样决定先对哪些Lagrange乘子进行优化。

两个Lagrange乘子的优化问题

首先回到我们前面一直悬而未解的问题，对偶函数最后的优化问题
$$\eqalign{ & \mathop {\max }\limits_{{\alpha _i} \ge 0} \sum\limits_{i = 1}^m {{\alpha _i}} - {1 \over 2}\sum\limits_{i,j = 1}^m {{\alpha _i}{\alpha _j}{y_i}{y_j}x_i^T{x_j}} \cr & s.t.{\rm{ }}\sum\limits_{i = 1}^m {{\alpha _i}} {y_i} = 0{\rm{, }}{\alpha _i} \ge 0{\rm{, }}i = 1,2,...,m \cr}$$

经过加入松弛变量，最终我们的问题变为
$$\eqalign{ &W(\alpha)= \max \sum\limits_{i = 1}^m {{\alpha _i}} - {1 \over 2}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {{\alpha _i}{\alpha _j}{y_i}{y_j}x_i^T} {x_j}} \cr & s.t.\sum\limits_{i = 1}^m {{\alpha _i}{y_i}} = 0,0 \le {\alpha _i} \le C,i = 1,2,...,m \cr}$$

要解决的问题是：在 $\alpha_i=\{\alpha_1,\alpha_2,,...,\alpha_n\}$ 上求上述目标函数的最大值。为此，每次任意抽取两个乘子 $\alpha_1$ 和 $\alpha_2$，固定其它乘子 $\{\alpha_3,\alpha_4,,...,\alpha_n\}$，使得目标函数只是关于 $\alpha_1$ 和 $\alpha_2$ 的函数。这样，不断的任意抽取两个，迭代求解子问题，最终达到求解原问题的目的。

下面讨论具体方法:
假设我们选取了初始值 $\{\alpha_1,\alpha_2,,...,\alpha_n\}$ 满足了问题中的约束条件。接下来，我们固定 $\{\alpha_3,\alpha_4,,...,\alpha_n\}$，这样 $W$ 就是 $\alpha_1$ 和 $\alpha_2$ 的函数。并且$\alpha_1$ 和 $\alpha_2$ 满足条件：

$$\alpha_1y^{(1)}+\alpha_2y^{(2)}=-\sum\limits_{i = 3}^m {{\alpha _i}y^{(i)}}$$

由于 $\{\alpha_3,\alpha_4,,...,\alpha_n\}$ 都是已知固定值，因此为了方面，可将等式右边标记成实数值 $\zeta$
$$\alpha_1y^{(1)}+\alpha_2y^{(2)}=\zeta$$

当$y^{(1)}$ 和$y^{(2)}$ 异号时，也就是一个为1，一个为-1时，他们可以表示成一条直线，斜率为1。如下图：
!
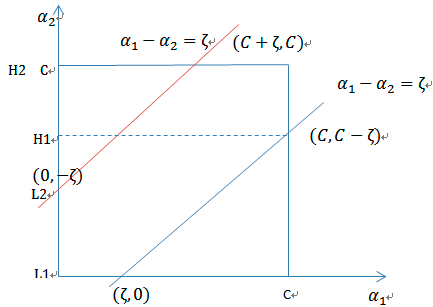
横轴是 $\alpha_1$，纵轴是 $\alpha_2$，$\alpha_1$ 和 $\alpha_2$既要在矩形方框内，也要在直线上。

如果 $\alpha_1$，$\alpha_2$ 满足上面红线 (此时 $\zeta <0$)，那么 $\alpha_2$的取值范围就是 $(-\zeta,C)$，即 $(\alpha_2-\alpha_1,C)$
如果 $\alpha_1$，$\alpha_2$ 满足下面蓝线 (此时 $\zeta >0$)，那么 $\alpha_2$的取值范围就是 $(0，C-\zeta)$，即 $(0，C-\alpha_1+\alpha_2)$
因为不知道满足红还是蓝线，所以 $\alpha_2$ 的取值范围是
$$L=max(0,\alpha_2-\alpha_1),H=min(C,C+\alpha_2-\alpha_1)$$

同理，当$y^{(1)}$ 和$y^{(2)}$ 同号时， $\alpha_2$ 的取值范围是
$$L=max(0,\alpha_2+\alpha_1-C),H=min(C,\alpha_1+\alpha_2)$$

然后我们打算将 $\alpha_1$ 用 $\alpha_2$ 表示
$$\alpha_1=(\zeta- \alpha_2y^{(2)})y^{(1)}$$
然后反代入$W$ 中，得
$$W(\alpha_1,\alpha_2,...,\alpha_m)=W((\zeta- \alpha_2y^{(2)})y^{(1)},\alpha_2,...,\alpha_m)$$
展开后 $W$ 可以表示成 $a\alpha_2^2+b\alpha_2+c$。其中 $a,b,c$ 是固定值。这样，通过对 $W$ 进行求导可以得到 $\alpha_2$，然而要保证 $\alpha_2$ 满足 $L \le \alpha_2 \le H$ ，我们使用 $\alpha_2^{new,unclipped}$ 表示求导求出来的 $\alpha_2$ ，然而最后的 $\alpha_2$ ，要根据下面情况得到：

$$\alpha _2^{new} = \left\{ {\matrix{ {H\matrix{ {} & {if{\rm{ }}\alpha _2^{new,unclipped} > H} \cr } } \cr {\alpha _2^{new,unclipped}\matrix{ {} & {if{\rm{ L}} \le \alpha _2^{new,unclipped} \le H} \cr } } \cr {L\matrix{ {} & {if{\rm{ }}\alpha _2^{new,unclipped} < L} \cr } } \cr } } \right.$$

这样得到 $\alpha_2^{new}$ 后，我们可以得到 $\alpha_1$ 的 新值 $\alpha_1^{new}$。

将 $\alpha_1$ 用 $\alpha_2$ 表示后代入 $W$ 中，得
$$\eqalign{ & \sum\limits_{i = 1}^m {{\alpha _i}} - {1 \over 2}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {{\alpha _i}{\alpha _j}{y_i}{y_j}{x_i}^T{x_j}} } \cr & = \sum\limits_{i = 1}^2 {{\alpha _i}} + \sum\limits_{i = 3}^m {{\alpha _i}} - {1 \over 2}\left( {\sum\limits_{i = 1}^2 {\left( {\sum\limits_{j = 1}^2 {{\alpha _i}{\alpha _j}{y_i}{y_j}{x_i}^T{x_j}} + \sum\limits_{j = 3}^m {{\alpha _i}{\alpha _j}{y_i}{y_j}{x_i}^T{x_j}} } \right)} + \sum\limits_{i = 3}^m {\left( {\sum\limits_{j = 1}^2 {{\alpha _i}{\alpha _j}{y_i}{y_j}{x_i}^T{x_j}} + \sum\limits_{j = 3}^m {{\alpha _i}{\alpha _j}{y_i}{y_j}{x_i}^T{x_j}} } \right)} } \right) \cr & = \sum\limits_{i = 1}^2 {{\alpha _i}} + \sum\limits_{i = 3}^m {{\alpha _i}} - {1 \over 2}\left( {\sum\limits_{i = 1}^2 {\left( {\sum\limits_{j = 1}^2 {{\alpha _i}{\alpha _j}{y_i}{y_j}{x_i}^T{x_j}} } \right)} + \sum\limits_{i = 1}^2 {\left( {\sum\limits_{j = 3}^m {{\alpha _i}{\alpha _j}{y_i}{y_j}{x_i}^T{x_j}} } \right)} + \sum\limits_{i = 3}^m {\left( {\sum\limits_{j = 1}^2 {{\alpha _i}{\alpha _j}{y_i}{y_j}{x_i}^T{x_j}} } \right)} + \sum\limits_{i = 3}^m {\left( {\sum\limits_{j = 3}^m {{\alpha _i}{\alpha _j}{y_i}{y_j}{x_i}^T{x_j}} } \right)} } \right) \cr & = \left( {\sum\limits_{i = 1}^2 {{\alpha _i}} - {1 \over 2}\sum\limits_{i,j = 1}^2 {{\alpha _i}{\alpha _j}{y_i}{y_j}{x_i}^T{x_j}} - \sum\limits_{i = 1}^2 {{\alpha _i}{y_i}\left( {\sum\limits_{j = 3}^m {{\alpha _j}{y_j}{x_i}^T{x_j}} } \right)} } \right) + \left( {\sum\limits_{i = 3}^m {{\alpha _i}} - {1 \over 2}\sum\limits_{i,j = 3}^m {{\alpha _i}{\alpha _j}{y_i}{y_j}{x_i}^T{x_j}} } \right) \cr & = {\alpha _1} + {\alpha _2} - {1 \over 2}{K_{11}}{\alpha _1}^2 - {1 \over 2}{K_{22}}{\alpha _2}^2 - s{K_{12}}{\alpha _1}{\alpha _2} - {y_1}{\alpha _1}{v_1} - {y_2}{\alpha _2}{v_2} + Const \cr }$$

其中
$${K_{ij}} = K({x_i},{x_j})\\ s=y_1y_2\\ {v_i} = \left( {\sum\limits_{j = 3}^m {{\alpha _j}{y_j}{x_i}^T{x_j}} } \right)\mathop { = = = = = = = = }\limits^{w = \sum\limits_{i = 1}^m {{\alpha _j}{y_j}{x_i}^T{x_j}} } f(x) - b - {y_1}{\alpha _1}^*{K_{1i}} - {y_2}{\alpha _2}^*{K_{2i}}$$

这里的 ${\alpha _1}^*$ 和 ${\alpha _2}^*$ 代表某次迭代前的原始值，因此是常数。
由于 ${\alpha _1}$ 和 ${\alpha _2}$ 满足以下公式
$$\alpha_1y^{(1)}+\alpha_2y^{(2)}={\alpha _1} ^*y^{(1)}+{\alpha _2}^*y^{(2)}=-\sum\limits_{i = 3}^m {{\alpha _i}y^{(i)}}$$
因为 ${\alpha _i}^*$ 的值是固定值，在迭代前后不会变。上式两边乘以 $y_1$，变为
$$\alpha_1+\alpha_2s={\alpha _1} ^*+{\alpha _2}^*s=T$$
其中 $T=-y_1\sum\limits_{i = 3}^m {{\alpha _i}y^{(i)}}$
代入上面目标函数得
$$W(\alpha _2)= {(T-\alpha _2s)} + {\alpha _2} - {1 \over 2}{K_{11}}{(T-\alpha _2s)}^2 - {1 \over 2}{K_{22}}{\alpha _2}^2 \\ - s{K_{12}}{(T-\alpha _2s)}{\alpha _2} - {y_1}{(T-\alpha _2s)}{v_1} - {y_2}{\alpha _2}{v_2} + Const$$

这时候只有 $\alpha _2$ 是变量了，求导
$$\eqalign{ & {{\partial W} \over {\partial {\alpha _2}}} = - s + 1 + {K_{11}}\left( {T - {\alpha _2}s} \right)s - {K_{22}}{\alpha _2} - s{K_{12}}\left( {\left( { - s} \right){\alpha _2} + \left( {T - {\alpha _2}s} \right)} \right) + {y_1}s{v_1} - {y_2}{v_2} \cr & = 1 - s + s{K_{11}}\left( {T - {\alpha _2}s} \right) - {K_{22}}{\alpha _2} + {K_{12}}{\alpha _2} - s{K_{12}}\left( {T - {\alpha _2}s} \right) + {y_2}{v_1} - {y_2}{v_2} \cr}$$
令导数为零，化简得到
$${\alpha _2}\left( {{K_{11}} + {K_{22}} - 2{K_{12}}} \right) = s\left( {{K_{11}} - {K_{12}}} \right)T + {y_2}\left( {{v_1} - {v_2}} \right) + 1 - s$$

将 $T$ 和 $v$ 代入后，继续化简推导，得
$${\alpha _2}\left( {{K_{11}} + {K_{22}} - 2{K_{12}}} \right) =\\$$

$$\eqalign{ & = {y_1}{y_2}\left( {{K_{11}} - {K_{12}}} \right)\left( {{\alpha _1}^* + {\alpha _2}^*{y_1}{y_2}} \right) + {y_2}\left( \matrix{ \left( {f({x_1}) - b - {y_1}{\alpha _1}^*{K_{11}} - {y_2}{\alpha _2}^*{K_{21}}} \right) \cr - \left( {f({x_2}) - b - {y_1}{\alpha _1}^*{K_{12}} - {y_2}{\alpha _2}^*{K_{22}}} \right) \cr} \right) + 1 - {y_1}{y_2} \cr & = \left( \matrix{ \left( {{y_1}{y_2}{K_{11}} - {y_1}{y_2}{K_{12}}} \right){\alpha _1}^* + \left( {{y_1}{y_2}{K_{11}} - {y_1}{y_2}{K_{12}}} \right){\alpha _2}^*{y_1}{y_2} + \cr \left( {{y_2}f({x_1}) - {y_2}{y_1}{\alpha _1}^*{K_{11}} - {\alpha _2}^*{K_{21}} - {y_2}f({x_2}) + {y_2}{y_1}{\alpha _1}^*{K_{12}} + {\alpha _2}^*{K_{22}}} \right) \cr} \right) + 1 - {y_1}{y_2} \cr & = {\alpha _2}^*\left( {{K_{11}} - 2{K_{12}} + {K_{22}}} \right) + {y_2}\left( {f({x_1}) - f({x_2}) + {y_2} - {y_1}} \right) \cr}$$

令
$$\eta= {{K_{11}} + {K_{22}} - 2{K_{12}}}$$
化简得 $${\alpha _2}\eta = {\alpha _2}^*\eta + {y_2}\left( {{E_1} - {E_2}} \right),{E_i} = f({x_i}) - {y_i}$$
两边都除以 $\eta$ 可以得到，更新
$${\alpha _2}^{new} = {\alpha _2}^* + {{{y_2}\left( {{E_1} - {E_2}} \right)} \over \eta }$$
与之前提到的一样 ${\alpha _2}^{new}$ 不是最终迭代后的值，需要进行约束
$${\alpha _2}^{new,clipped} = \left\{ {\matrix{ {H\matrix{ {} & {{\rm{if }}{\alpha _2}^{new} \ge H} \cr } } \cr {{\alpha _2}^{new}\matrix{ {} & {{\rm{if L}} \le {\alpha _2}^{new} \le H} \cr } } \cr {L\matrix{ {} & {{\rm{if }}{\alpha _2}^{new} \le L} \cr } } \cr } } \right.$$

那么
$${\alpha _1}^{new} = {\alpha _1} + s\left( {{\alpha _2} - {\alpha _2}^{new,clipped}} \right)$$
至此，迭代关系式除了 $b$ 的推导式以外，都已经推出。

下面来找到求 $b$ 值的公式和启发式搜索方法
$b$ 每一步都要更新，因为前面的KKT条件指出了 $\alpha_i$ 和 $y_i\mu_i$的关系，而 $\mu_i$ 和 b<script type="math/tex">b</script> 有关，在每一步计算出 $\alpha_i$ 后，根据KKT条件来调整 $b$。

b的更新有几种情况：

启发式搜索方法
类似的，对软间隔支持向量机，KKT条件要求为
$$\left\{\matrix{ &\alpha_i\ge{0}, \mu_{i}\ge{0}\\ &{y_i}f(x_i)-1+{\xi _i} {\rm{ }}\ge{0}\\ &{\alpha _i}({y_i}f(x_i)-1+{\xi _i} {\rm{ }})=0 \\ &{\xi_i} \ge0, \mu_i{\xi_i}= 0 \\ } \right.$$

对于任意样本，总有 $\alpha_i=0$ 或者 ${y_i}f(x_i)=1-{\xi _i} {\rm{ }}$。

1、若 $\alpha_i=0$ ，则 ${y_i}f(x_i)>1-{\xi _i} {\rm{ }}$，由 $C = {\alpha _i} + {\mu _i}$ 知 ${\mu _i=C}$，进而 $\xi _i=0$，得 ${y_i}f(x_i)>1$，表明 $\alpha_i$ 是正常分类，在边界内部。

2、若 $0<\alpha_i<C$ ，则必有 ${y_i}f(x_i)=1-{\xi _i} {\rm{ }}$，由 $C = {\alpha _i} + {\mu _i}$ 知 ${\mu _i>0}$ 进而 $\xi _i=0$， 得${y_i}f(x_i)=1$，表明 $\alpha_i$ 是支持向量，在边界上。

3、若 $\alpha_i=C$ ，$C = {\alpha _i} + {\mu _i}$ 知 ${\mu _i=0}$ 进而 $\xi _i>0$，由 ${y_i}f(x_i)=1-{\xi _i}$ 得 ${y_i}f(x_i)<1$，表明 $\alpha_i$ 是在两条边界之间。

而最优解需要满足KKT条件，即上述3个条件都得满足， 所以要找出不满足KKT条件的这些 ${\alpha _i}$，并更新这些 ${\alpha _i}$。由于这些 ${\alpha _i}$ 受到约束
$$\sum\limits_{i = 1}^m {{\alpha _i}{y_i}} = 0$$
因此，我们通过同时更新 ${\alpha _i}$ 和 ${\alpha _j}$ ，要求满足以下等式
$${\alpha _i}y_i+ {\alpha _j}y_j=Const$$
就能保证和为0的约束。

所谓的启发式选择方法主要思想是每次选择拉格朗日乘子时，优先选择样本前面系数 $0<\alpha_i<C$ 的 $\alpha_i$ 作优化，因在界上的样例对应的系数 $\alpha_i$ 一般不会更改。

这条启发式搜索方法是选择第一个拉格朗日乘子用的，比如前面的 $\alpha_2$。那么这样选择的话，是否最后会收敛。可幸的是Osuna定理告诉我们只要选择出来的两个 $\alpha_i$ 中有一个违背了KKT条件，那么目标函数在一步迭代后值会减小。违背KKT条件不代表 $0<\alpha_i<C$ ，在界上也有可能会违背。是的，因此在给定初始值 $\alpha_i=0$后，先对所有样例进行循环，循环中碰到违背KKT条件的（不管界上还是界内）都进行迭代更新。等这轮过后，如果没有收敛，第二轮就只针对 $0<\alpha_i<C$ 的样例进行迭代更新。

在第一个乘子选择后，第二个乘子也使用启发式方法选择，第二个乘子的迭代步长大致正比于 $\left| {{E_1} - {E_2}} \right|$ ，选择第二个乘子能够最大化 $\left| {{E_1} - {E_2}} \right|$ 。即当 $E_1$ 为正时选择负的绝对值最大的 $E_2$ ，反之，选择正值最大的 $E_2$ 。

最后的收敛条件是在界内（ $0<\alpha_i<C$ ）的样例都能够遵循KKT条件，且其对应的 $\alpha_i$ 只在极小的范围内变动。

支持向量回归

核方法