红黑树的变色与旋转

wangliang888888

已于 2023-09-07 15:19:22 修改

阅读量247

点赞数

文章标签： linux 算法

于 2023-09-07 15:15:26 首次发布

原文链接：https://blog.csdn.net/jinking01/article/details/106020347

版权

红黑树插入操作

红黑树之所以叫红黑树，是因为它有这些约束：
1.节点要么是红色要么是黑色
2.根节点必须是黑色
3.叶子节点挂两个空节点(逻辑上)是黑色
4.每个红色节点有两个黑色子节点，推导出一条路径上不能有两个连续的红色节点
5.每条路径上必须有相同数量的黑色节点
每一条规则都很简单，并且它们都在讲颜色的限制，正符合红黑树这个名字。

红黑树插入操作分类分析

我们开始做插入操作：默认新插入的节点是红色。

不需要做任何变色或者旋转的情况：
新插入的节点父节点是黑色，皆大欢喜。

需要做变色的情况：
1.新插入的节点是根节点，根据rule2,颜色变成黑色，相当简单。
2.如果它的父节点也是红色，违反了rule4，此时如果发现叔节点也是红色，那么将父与叔节点标记为黑色，祖节点为红色，然后把祖节点当作新插入的节点递归重复这一判断，直到根节点，将根节点颜色设置为黑色。

需要做变色与旋转的情况：
当叔节点是黑色，需要做旋转，这是此文的重点，分为以下4中情况。
我们一般会使用左左，右右，左右，右左来表示插入节点与父节点所在的位置，然后根据这些位置来做旋转的应用。文字通常是难记的，放弃文字描述，而使用符号以及图像来记忆：
左左：/ 一根斜线(此时最好用手比划一下)，顶点表示祖节点，中间点表示父节点，底点表示插入节点
右右: \ 一根反斜线，表示同上
左右：< 一个小于号，顶点表示祖节点，中间尖点表示父节点，底点表示插入节点
右左：> 一个大于号，表示同上

红黑树是一棵平衡树，保持结构平衡是其存在的根本意义，而一根”斜线“或者“反斜线”，一个“小于号”或“大于号”，以底部为支持是无法保持平衡的，如果让其转变成一个三角型:⋀，那便是平衡的。
那么对于“斜线”，把祖节点扳下来，怎么扳？你用右手向下扳最方便，让/变成⋀，所谓右旋；最后父节点颜色变成黑色，祖节点颜色变成红色；父节点为当前节点，递归进行变色或者旋转的判断。
在这里插入图片描述
对于“反斜线”，你用左手向下扳祖节点，让\变成⋀，所谓左旋。

对于“小于号”，我们不能一步到位，直接把<旋转变成⋀，因为这会涉及到三个节点交换位置，而是先把它扳直，变成一根斜线。扳直首先想到的是让新插入的节点作为父节点的左节点，但是这是不可能的，新插入的节点肯定比父节点值大，这是二叉搜索树的根本；因为父节点比新插入节点小，那么只能让父节点成为新插入节点的左节点，也就说让父子节点互换位置，此是形状变成了/，然后根据”斜线“规则去旋转。
在这里插入图片描述
对于”大于号“，思路与旋转“小于号”相同，父节点作为新插入节点的右节点，新插入节点代替原父节点位置，最后进行变色，以及递归判断变色或者旋转。

旋转完成之后，再根据变色原则，进行变色，这个过程中同样也会遇到旋转，但你已经明白了旋转的规律了。
这是一篇与众不同的红黑树介绍文章，它没有介绍基础，也没有任何代码，甚至没有红黑树，但我相信，你已经明白了红黑树的旋转要点了。

插入详解

情况1：uncle 存在（uncle != null），并且 uncle 的颜色是红色

节点插入后处理方法（仅变色）：grandpa 由黑变红，parent & uncle 由红变黑；
在这里插入图片描述

情况2：uncle 不存在，或者 uncle 存在但是颜色是黑色（分为以下四种情况）

情况2.1：cur 是 parent 左孩子，且 parent 是 grandpa 的左孩子**
节点插入后处理方法： grandpa 右旋之后颜色变为红色，parent 的颜色变为黑色
在这里插入图片描述
情况2.2：cur 是 parent 的右孩子，且 parent 是grandpa 的右孩子
节点插入后处理方法：grandpa 左旋后颜色变为红色，parent 颜色变为黑色

情况2.3：cur 是 parent 的右孩子，parent 是 grandpa 的左孩子
节点插入后处理方法：对 parent 左旋之后将 parent 和 cur 的名称交换，再按照2.1的情况处理
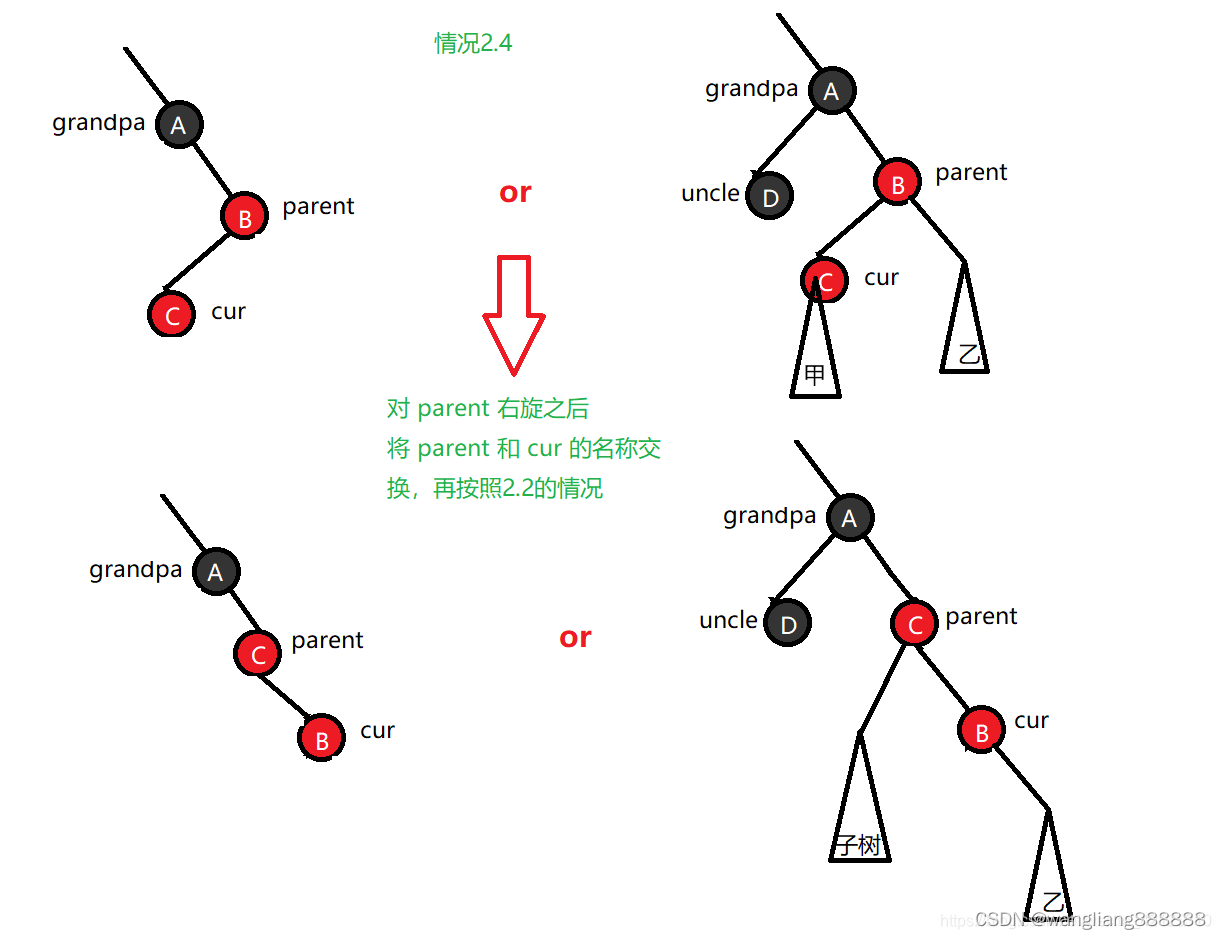
在这里插入图片描述
情况2.4： cur 是 parent 的左孩子，parent 是 grandpa 的右孩子
节点插入后处理方法：对 parent 右旋之后将 parent 和 cur 的名称交换，再按照2.2的情况处理

本文转自：https://blog.csdn.net/jinking01/article/details/106020347，
https://zhuanlan.zhihu.com/p/102693409#:~:text=%E7%BA%A2%E9%BB%91%E6%A0%91%E7%9A%84%E5%8F%98%E8%89%B2%E4%B8%8E%E6%97%8B%E8%BD%AC%201%20%E8%8A%82%E7%82%B9%E8%A6%81%E4%B9%88%E6%98%AF%E7%BA%A2%E8%89%B2%E8%A6%81%E4%B9%88%E6%98%AF%E9%BB%91%E8%89%B2%202%20%E6%A0%B9%E8%8A%82%E7%82%B9%E5%BF%85%E9%A1%BB%E6%98%AF%E9%BB%91%E8%89%B2%203,%E5%8F%B6%E5%AD%90%E8%8A%82%E7%82%B9%E6%8C%82%E4%B8%A4%E4%B8%AA%E7%A9%BA%E8%8A%82%E7%82%B9%20%28%E9%80%BB%E8%BE%91%E4%B8%8A%29%E6%98%AF%E9%BB%91%E8%89%B2%204%20%E6%AF%8F%E4%B8%AA%E7%BA%A2%E8%89%B2%E8%8A%82%E7%82%B9%E6%9C%89%E4%B8%A4%E4%B8%AA%E9%BB%91%E8%89%B2%E5%AD%90%E8%8A%82%E7%82%B9%EF%BC%8C%E6%8E%A8%E5%AF%BC%E5%87%BA%E4%B8%80%E6%9D%A1%E8%B7%AF%E5%BE%84%E4%B8%8A%E4%B8%8D%E8%83%BD%E6%9C%89%E4%B8%A4%E4%B8%AA%E8%BF%9E%E7%BB%AD%E7%9A%84%E7%BA%A2%E8%89%B2%E8%8A%82%E7%82%B9%205%20%E6%AF%8F%E6%9D%A1%E8%B7%AF%E5%BE%84%E4%B8%8A%E5%BF%85%E9%A1%BB%E6%9C%89%E7%9B%B8%E5%90%8C%E6%95%B0%E9%87%8F%E7%9A%84%E9%BB%91%E8%89%B2%E8%8A%82%E7%82%B9