逻辑回归(Logistic Regression)

最新推荐文章于 2024-05-19 14:00:00 发布

futurewq

最新推荐文章于 2024-05-19 14:00:00 发布

阅读量5.4k

点赞数 4

分类专栏： machine learning

原文链接：https://zhuanlan.zhihu.com/p/74874291?utm_source=com.youdao.note

版权

machine learning 专栏收录该内容

13 篇文章 0 订阅

订阅专栏

1.模型介绍

Logistic Regression虽然被称为回归，但其实实际上是分类模型，并常用于二分类。Logistic Regresion因其简单、可并行化、可解释强深受工业界喜爱。

Logistic回归的本质是：假设数据服从这个分布，然后使用极大似然估计做参数的估计。

1.1Logistic分布

Logistic分布是一种连续型的概率分布，其分布函数和密度函数分别为:
$F(x)=P(X\leqslant x)=\frac{1}{1+e^{-(x-\mu )/\gamma )}}$

$f(x) = {F}'(X\leq x)=\frac{e^{-(x-\mu )/\gamma }}{\gamma (1+e^{-(x-\mu )/r})^{2}}$

其中，μ表示位置参数，γ>0为形状参数。我们可以看下其图像特征：

Logistic分布是由其位置和尺度参数定义的连续分布。Logistic分布的形状与正态分布的形状相似，但是Logistic分布的尾部更长，所以我们可以使用Logistic分布来建模比正态分布具有更长尾部和更高波峰的数据分布。在深度学习中常用的Sigmoid函数就是Logistic的分布函数在μ=0，γ=1的特殊形式。

1.2Logisitic回归

之前说到Logistic回归主要用于分类问题，我们以二分类为例，对于所给数据集假设存在这样一条直线可以将数据完成线性可分。

决策边界可以表示为 $w{_{1}}x{_{1}}+w{_{2}}x{_{2}}+b=0$ ,假设某个样本点 $h{_{w}}(x)=w{_{1}}x{_{1}}+w{_{2}}x{_{2}}+b>0$ ,那么可以判断它的类别为1，这个过程其实就是感知机。

Logistic回归还需要加一层，它要找到分类概率P(Y=1)与输入向量x的直接关系，然后通过比较概率值来判断类别。

考虑二分类问题，给定数据集

$D=(x{_{1}},y{_{1}}),(x{_2},y_2),...,(x_N,y_N),x_i\subseteq R^n,y_i\in 0,1,i=1,2,...,N$

考虑到 $w^Tx+b$ 取值是连续的，因此它不能拟合离散变量。可以考虑用它来拟合条件概率p(Y=1|x)，因此概率的取值也是连续的。

但是对于w!=0(若等于零向量则没有什么求解的价值), $w^Tx+b$ 取值为R，不符合概率取值为0到1，因此考虑采用广义线性模型。

最理想的是单位阶跃函数：

$p(y=1|x)=\left\{\begin{matrix} 0,z<0& \\ 0.5,z=0& \\ 1,z>0& \end{matrix}\right.$

$z=w^Tx+b$

但是这个阶跃函数不可微，对数几率函数是一个常用的替代函数：

$y=\frac{1}{1+e^{-(w^Tx+b)}}$

于是有：

$ln(\frac{y}{1-y})=w^Tx+b$

我们将y视为x为正例的概率，则1-y为x为其反例的概率。两者的比值称为几率，指该事件发生与不发生的概率比值，若事件发生的概率为p。则对数几率：

$ln(odds)=ln\frac{y}{1-y}$

将y视为类后验概率估计，重写公式有：

$w^Tx+b=ln\frac{P(Y=1|x)}{1-P(Y=1|x)} \\ P(Y=1|x)=\frac{1}{1+e^{-(w^Tx+b)}}$

也就是说，输出Y=1的对数几率是由输入x的线性函数表示的模型，这就是逻辑回归模型。当 $w^Tx+b$ 的值越接近正无穷，P(Y=1|x)概率值也就越接近1.因此逻辑回归的思路是，先拟合决策边界(不局限与线性，还可以是多项式)，再建立这个边界与分类的概率联系，从而得到二分类情况下的概率

在这我们思考个问题，我们使用对数几率的意义在哪?通过上述推导我们可以看到Logistic回归实际上是使用线性回归模型的预测值逼近分类任务真实标记的对数几率，其优点有：

1。直接对分类的概率建模，无需实现假设数据分布，从而避免了假设分布不准确带来的问题(区别于生成式模型)

2.不仅可预测出类别，还能得到该预测的概率，这对一些利用概率辅助决策的任务是很有用

3.对数几率函数是任务阶可导的凸函数，有许多数值优化算法都可以求出最优解。

1.3代价函数

逻辑回归模型的数学形式确定后，剩下就是如何去求解模型中的参数。在统计学中，常常使用极大似然估计法来求解，即找到一组参数，使得在这组参数下，我们的数据的似然度最大。

设：
$P(Y=1|x)=p(x)\\ P(Y=0|x)=1-p(x)$

似然函数：

$L(w)=\prod {[p(x_i)]^{y_i}}[1-p(x_i)]^{1-y_i}$

为了更方便求解，我们对等式两边同时取对数，写成对数似然函数：

$lnL(w)=\sum [{y_i}lnp(x_i)+(1-y_i)ln(1-p(x_i))]\\ =\sum [{y_i}ln\frac{p(x_i)}{1-p(x_i)}+ln(1-p(x_i))]\\ =\sum [{y_i}(w\cdot {x_i})-ln(1+e^{w\cdot {x_i}})]$

在机器学习中我们有损失函数的概念，其衡量的是模型预测错误的程度。如果取整个数据集上的平均对数似然损失，我们可以得到：

$J(w)=-\frac{1}{N}lnL(w)$

即在逻辑回归模型中，我们最大化似然函数和最小化损失函数实际上是等价的。

1.4求解

求解逻辑回归的方法有非常多，这里主要聊下梯度下降和牛顿法。优化的主要目标是找到一个方向，参数朝这个方向移动之后使得损失函数的值能够减小，这个方向往往由一阶偏导或者二阶偏导各种组合求得。逻辑回归的损失函数是：

$J(w)=-\frac{1}{n}(\sum_{i=1}^{n}({y_i}lnp(x_i)+(1-y_i)ln(1-p(x_i))))$

1.随机梯度下降

2.牛顿法

1.5正则化

正则化是一个通用的算法和思想，所有会产生过拟合现象的算法都可以使用正则化来避免过拟合。

在经验风险最小化的基础上(即训练误差最小化)，尽可能采用简单的模型，可以有效提高泛化预测精度。如果模型过于复杂，变量值稍微有点变动，就会引起预测精度问题。正则化之所以有效，就是因为其降低了特征的权重，使得模型更为简单。、

正则化一般会采用L1范式或者L2范式，其形式分别为 $\Phi (w)=||x||_1,\Phi(w)=||x||_2$

1.L1正则化

Lasso回归，相当于为模型添加了这样一个先验知识：w服从零均值拉普拉斯分布。首先看看拉普拉斯分布长什么样子：
$f(w|\mu ,b)=\frac{1}{2b}exp(-\frac{|w-\mu|}{b})$

由于引入了先验知识，所以似然函数这样写：

$L(w)=P(y|w,x)P(w)\\ = \prod_{i=1}^{N}p(x_i)^{y_i}(1-p(x_i))^{1-y_i}\prod_{j=1}^{d}\frac{1}{2b}exp(-\frac{|w_j|}{b})$

取log再取负，得到目标函数：

$-lnL(w)=-\sum_{i=1}^{N}[{y_i}lnp(x_i)+(1-y_i)ln(1-p(x_i))]+\frac{1}{2{b_2}}\sum_{j=1}^{d}|w_j|$

等价于原始损失函数的后面加上了L1正则，因此L1正则的本质其实就是为模型增加了“模型参数服从零均值拉普拉斯分布”这一先验知识

2.L2正则化

Ridge回归，相当于为模型添加了这样一个先验知识：w服从零均值正态分布

首先看看正态分布的样子：

$f(w|\mu,\sigma)=\frac{1}{\sqrt{2}\sigma}exp(-\frac{(w-\mu)^2}{2\sigma^2})$

由于引入了先验知识，所以似然函数可以这样写：

$L(w)=P(y|w,x)P(w)\\ = \prod_{i=1}^{N}{p(x_i)}^{y_i}(1-p(x_i))^{(1-y_i)}\prod_{j=1}{d}\frac{1}{\sqrt{2\pi }\sigma}exp(-\frac{w_j^{2}}{2\sigma^2})\\ =\prod_{i=1}^{N}{p(x_i)}^{y_i}(1-p(x_i))^{(1-y_i)}\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{w^Tw}{2\sigma^2})$

取ln再取负，得到目标函数：

$-lnL(w)=-\sum_{i=1}^{N}[y_ilnp(x_i)+(1-y_i)ln(1-p(x_i))]+\frac{1}{2\sigma^2}w^Tw$

等价于原始的损失函数后面加上了L2正则，因此L2正则的本质其实是为模型增加了"模型参数服从零均值正态分布"这一先验知识。

3.L1和L2的区别

从上面的分析中我们可以看到，L1正则化增加了所有权重w参数的绝对值之和逼迫更多w为零，也就是变稀疏(L2因为其导数也趋哦，奔向零的速度不如L1给力了)。我们对稀疏规则趋之若鹜的有个关键原因在于它能实现特征的自动选择。一般来说，大部分特征x_i都是和最终的输出y_i没有关系或者不提供任何信息的。在最小化目标函数的时候考虑x_i这些额外的特征，虽然可以获得更小的训练误差，但在预测新的样本时，这些没用的特征权重反而会被考虑，从而干扰了对正确y_i的预测。L1正则化的引入就是为了完成特征自动选择的光荣使命，它会学习地去掉这些无用的特征，也就是把这些特征对应的权重置为0.

L2正则化中增加所有权重w参数的平方之和，逼迫所有w尽可能趋于0但不为0(L2的导数趋于零)。因为在未加入L2正则化发生过拟合时，拟合函数会顾虑每个点，最终形成的拟合函数波动很大，在某些很小的区间里，函数值的变化很剧烈，也就是某些w值非常大。为此，L2正则化的加入就惩罚了权重变大的趋势。

我们以二维样本为例，图解阐述加入L1正则化和L2正则化之后目标函数求解时发生的变化。

。。。原函数曲线等高线(同颜色曲线上，每一组w1,w2带入后值都相同)

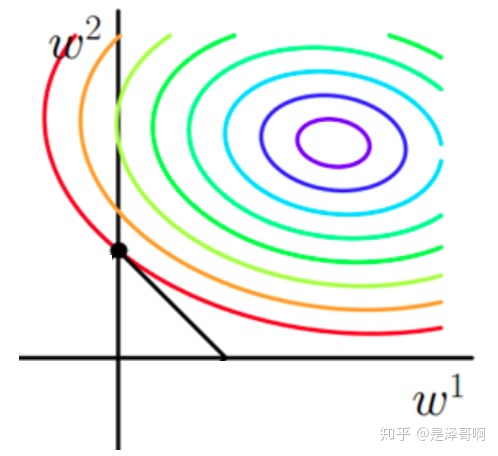
preview

那现在我们看下加了L1正则化和L2正则化之后，目标函数求解的时候，最终解会有什么变化。

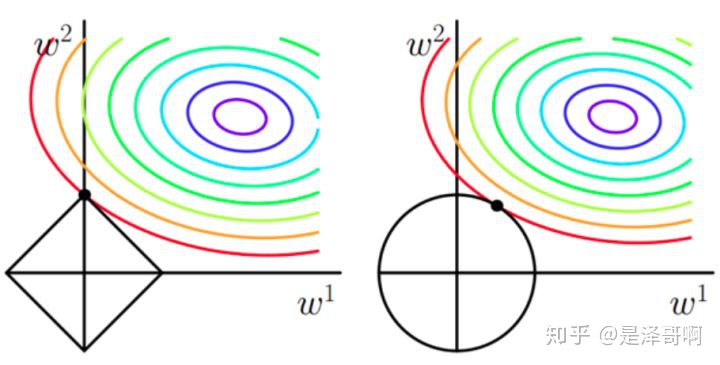
preview

从上边两幅图中我们可以看出：

。。。如果不加L1和L2正则化的时候，对于线性回归这种目标函数凸函数的话，我们最终的结果就是最里面的紫色的小圈圈等高线上的点。

。。。当加入L1正则化的时候，我们先画出|w1|+|w2|=F的图像，也就是一个菱形，代表这些曲线上的点算出来的L1范数|w1|+|w2|都为F.那我们现在的目标是不仅是原曲线算的值要小(越来越接近中心的紫色圈圈)，还要使得这个菱形越小越好(F越小越好)。那么还和原来一样的话，过中心紫色圈圈的那个菱形明显很大。因此我们要取到一个恰好的值。那么如何求值呢？

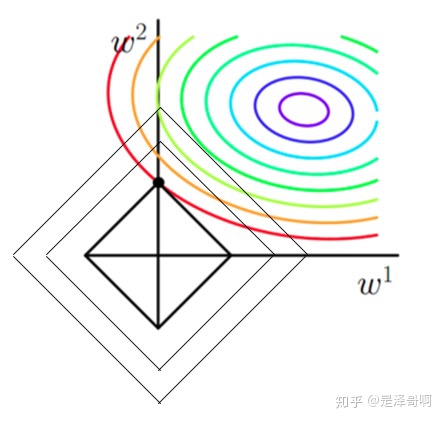
preview

1.以同一条原曲线目标等高线来说，现在以最外圈的红色等高线为例，我们看到，对于红色曲线上的每个点都可做一个菱形，根据上图可知，当这个菱形与某条等高线相切(仅有一个交点)的时候，这个菱形最小。用公式说这个时候能使得在相同得 $\frac{1}{N}\sum_{i=1}^{N}(y_i-w^Tx_i)^2$ ,由于相切得时候的 $C||w||_1$ ，即|w1|+|w2|所以能够使得 $\frac{1}{N}\sum_{i=1}^{N}(y_i-w^Tx_i)^2+C||w||_1$ 更小。

2.有了第一条的说明我们可以看出，最终加入L1范数得到的解一定是某个菱形和某条原函数等高线的切点。现在有个比较重要的结论来了，我们经过观察发现，几乎对于很多原函数等高曲线，和某个菱形相交的时候及其容易相交在坐标轴(比如上图)，也就是说最终的结果，解的某些维度及其容易是0，比如上图最终解是w=(0,x),这也就是我们所说的L1更容易得到稀疏解(解向量中0比较多)的原因；

3.当然光看着图说，L1的菱形更容易和等高线相交在坐标轴一点过都没说服力，只是个感性的认识，我们接下来从更严谨的方式来证明，简而言之就是假设现在我们是一维的情况下h(w)=f(w)+C|w|，其中h(w)是目标函数，f(w)是没加L1正则化项前的目标函数，C|w|是L1正则项，要使得0点成为最值可能的点，虽然在0点不可导，但是我们只需要让0点左右的导数异号，即即可也就是C>|f'(0)|的情况下，0点都是可能的最值点。

当加入L2正则化的时候，分析和L1正则化是类似的，也就是说我们仅仅是从菱形变成了圆形而已，同样还是求原曲线和圆形的切点作为最终解。当然与L1范数比，我们这样求得L2范数得从图上来看，不容易交在坐标轴上，但是仍然比较靠近坐标轴。因此这也就是我老说得，L2范数额能让解比较小(靠近0)，但是比较平滑(不等于0)

综上所述，我们可以看见，加入正则化项，在最小化经验误差的情况下，可以让我们选择解更简单(趋向于0)的解。

结构风险最小化：在经验风险最小化的基础上(也就是训练误差最小化)，尽可能采用简单的模型，以此提高泛化预测精度。

因此，加正则化项就是结构风险最小化的一种实现。

正则化之所以能够降低过拟合的原因在于，正则化是结构风险最小化的一种策略实现。

简单总结：

给loss function加上正则化项，能使新得到的优化目标函数h=f+||w||,需要在f和||w||中做一个权衡，如果还像原来只优化f的情况下，那可能得到一组解比较复杂，使得正则化项目||w||比较大，那么h就不是最优的，因此可以看出加上正则项能让解更加简单，符合奥卡姆剃刀理论，同时也比较符合在偏差和方差（方差表示模型的复杂度）分析中，通过降低模型复杂度，得到更小的泛化误差，降低过拟合程度。

L1正则化就是在loss function后边加正则项为L1范数，加上L1范数容易得到稀疏解(0比较多)。L2正则化就是loss function 后边加正则项为L2范数的平方，加上L2正则相比于L1正则来说，得到的解比较平滑(不是稀疏)，但是同样能够保证解中接近于0(但不是等于0，所以相对平滑)的维度比较多，降低模型的复杂度。

逻辑回归详解

futurewq

关注

4
点赞
踩
22

收藏

觉得还不错? 一键收藏
0
评论
逻辑回归(Logistic Regression)

1.模型介绍Logistic Regression虽然被称为回归，但其实实际上是分类模型，并常用于二分类。Logistic Regresion因其简单、可并行化、可解释强深受工业界喜爱。Logistic回归的本质是：假设数据服从这个分布，然后使用极大似然估计做参数的估计。1.1Logistic分布Logistic分布是一种连续型的概率分布，其分布函数和密度函数分别为:其中，μ表示位置参数，γ>0为形状参数。我们可以看下其图像特征：Logistic分布是由其位置和尺度参数定义
复制链接

扫一扫