LogisticRegression(逻辑回归)

一：概念

Logistic Regression 虽然被称为回归，但其实际上是分类模型，并常用于二分类。Logistic Regression 因其简单、可并行化、可解释强深受工业界喜爱。
Logistic 回归的本质是：假设数据服从这个分布，然后使用极大似然估计做参数的估计。

决策边界可以表示为​ ：

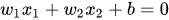
1.对未知样本
$$x=(x_1+x_2...x_n)$$类别的预测 与 求解：w
$$\begin{gathered} z=w^{T}x=w_0+w_1{x}_1+w_2{x}_2+...+w_n{x}_n+b \\ 矩阵格式为： \\ z=w^{T}x=\begin{array}{c}\left[\begin{array}{c}{w}_0\\ w_1\\ w_2\\ ...\\ w_n\end{array}\right]\left[\begin{array}{ccccc}1& x_1& x_2& ...& x_n\end{array}\right]\end{array} \\ 注意：x向量第一个元素为1，后面代码会有生成过程。 \end{gathered}$$

2.将特征的现行组合函数通过sigmoid函数进行归一化
$$sigmoidfunction：\phi (z)=\frac{1}{1+e^{-z}}$$
那么 ~
$$x属于正类的概率\hat{p}=\{\begin{array}{r}1(\hat{p}\le 0.5)\\ 0(\hat{p}<0.5)\end{array}$$
$$sigmoid:$$

• sigmoid 函数输出概率的形式值域为（0，1），因为一般处理二分问题我们只需要两个预测值，当然我也见过（-1，1）不确定是否还是sigmoid函数，但是后面的数学公式全部需要重推而且概率也不是我们想要的了 ps：这个还有待考究，十分麻烦，所以还是采用（0，1）区间。
• 样本x各个维度的加权叠加z作为sigmoid的输入
  $$z\in (-\infty ,+\infty ),z=0\phi (z)=0.5$$
  2.推导进行分类公式
  $$\frac{p}{1-p}几率(odds)$$
  $$log(\frac{p}{1-p})对数几率(logodds)或logit$$
• x为正例的概率越大那么对数几率取值就越大， 相反取反例的概率越大对数的几率取值就越小
• 取得线性模型：
  $$log(\frac{p}{1-p})=w^{T}x+b$$
• 那么正反例的推导就为：
  $$p(y=1|x)=\phi (x)=\frac{1}{1+e^{-w^{T}x+b}}$$
  $$p(y=0|x)=\phi (x)=\frac{e^{-w^{T}x+b}}{1+e^{-w^{T}x+b}}$$
• 现在我们来讨论单个训练样本的代价函数
  $$例如：(x^{(i)},y^{(i)})$$
  $$L(w,b)=\{\begin{array}{r}-log(\hat{p})(y^{(i)}=1)\\ -log(1-\hat{p})(y^{(i)}=0)\end{array}$$
  $$\begin{gathered} 当y^{(i)}=1时，\hat{p}值越小，训练样本是正类的可能性越小，将其判断为正类的代价就越高 \\ 当y^{(i)}=0时，\hat{p}值越大，训练样本是负类的可能性越小，将其判断为负类的代价就越高 \end{gathered}$$
• 总代价函数：
  $$cost=L(w,b)=-[y^{(i)}log(\hat{p})+(1-y^{(i)})log(1-\hat{p})]$$
  $$\begin{gathered} cost对w求偏导得（此处使用梯度下降法求最优w）： \\ \frac{\partial cost}{\partial w}=x^T(\frac{1}{1+e^{-z}}-y^{(i)}) \end{gathered}$$
• 使用梯度下降求最优w
  1.初始化w （w为三行一列矩阵）
  2.更新w：
  $$w=-alpha\ast \frac{\partial cost}{\partial w}$$
  3.迭代到一定次数或到一定阀值
• 最后得到w为一条超平面线将正利反例分割开
  

python代码：

import os, sys
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
#从文本中读取
x = []
y = []
label = []
len1 = 0
index = 0
file_path = 'testSet.txt'
data_dir = '.'
file_path = os.path.join(data_dir, file_path)
data = [line.strip() for line in open(file_path)]
np.random.shuffle(data)
for data1 in data:
    part_x, part_y, part_label = data1.split(' ')
    x.append(float(part_x))
    y.append(float(part_y))
    label.append(int(part_label))
    len1 = len1 + 1
#print(label)
#concatenate函数主要指的是吧x按照0轴进行合并

"""
#从sklearn dataset中读取数据
iris = datasets.load_iris()
x = iris['data'][0]
y = iris['target']
x = x[y != 2]
y = y[y != 2]
"""

x = np.concatenate([x])
x = x.reshape(len1,1)
#print(x)
y = np.concatenate([y])
y = y.reshape(len1,1)

#X与一个len1行1列的矩阵合并
ones = np.ones((len1, 1))
x = np.hstack((x,ones))
x = np.hstack((x, y))
#print(x)
x_avr = np.mean(x)
x_std = np.std(x)

label = np.concatenate([label])
label = label.reshape(len1,1)

for label1 in label:
    if(label1 == 0):
        plt.scatter(x[index,0], y[index,0], c='red')
    elif(label1 == 1):
        plt.scatter(x[index,0], y[index,0], c='green')
    index = index + 1

def sigmoid(x, omega):
    diff = np.dot(x,omega)
    return 1 / (1 + np.exp(-diff))

def cost(label, sig):
    return (1./len1) * (np.dot(-label, np.log(sig)) - np.dot((1 - label), np.log(1 - sig)))

def gradient(x, label, sig):
    gradient = (1./len1) * (np.dot(np.transpose(x), (sig - label)))
    return gradient

def Logistic_regression(x, label):
    num = 100000  #迭代2000000轮
    omega = np.array([0, 0, 0]).reshape(3, 1)
    alpha = 0.01
    sig = sigmoid(x, omega)
    cost_gradient = gradient(x, label, sig)
    for i in range(num):
        omega = omega - alpha * cost_gradient
#        print(omega)
        sig = sigmoid(x, omega)
        cost_gradient = gradient(x, label, sig)
    return omega

omega = Logistic_regression(x, label)
x1 = np.linspace(-5, 5, 100)   #创建一个等差数列
y1 = (omega[0]*x1 + omega[1]) / -omega[2]
print(omega)
plt.plot(x1, y1)
plt.show()

数据格式：
数据集大家可以模拟一下 类似
x1 x2 lable
1 3 0
2 5 1
这种 也可以在sklearn.datasets 中使用预制的数据集。

• 之后会继续完善文档 ， 此种还有细节和正则化问题需要补充！！！