
程序循环里主要的部分是枚举树 而不是猴子 !
用f[i][j]来表示前 i 只猴子上了前 j 课树
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
const long long maxn = 5005 ;
long long n,mon[maxn],tree[maxn],m,f[3][maxn];
int main()
{
scanf("%d",&n) ;
for(long long i = 1;i <= n ;++i) scanf("%d",&mon[i]) ;
scanf("%d",&m) ;
for(long long i = 1;i <= m ;++i) scanf("%d",&tree[i]) ;
sort(mon + 1,mon + n + 1) ;
sort(tree + 1,tree + m + 1) ;
memset(f,0x7f,sizeof(f)) ;
f[1][1] = abs(mon[1] - tree[1]) ;
for(long long i = 2;i <= n ;++i)
for(long long j = 1;j <= m ;++j) {
f[i % 2][j] = min(f[(i - 1 ) % 2][j] , f[(i - 1 ) % 2][j - 1]) + abs(mon[i] - tree[j]) ;
}
cout<<f[n % 2][m] ;
return 0;
}










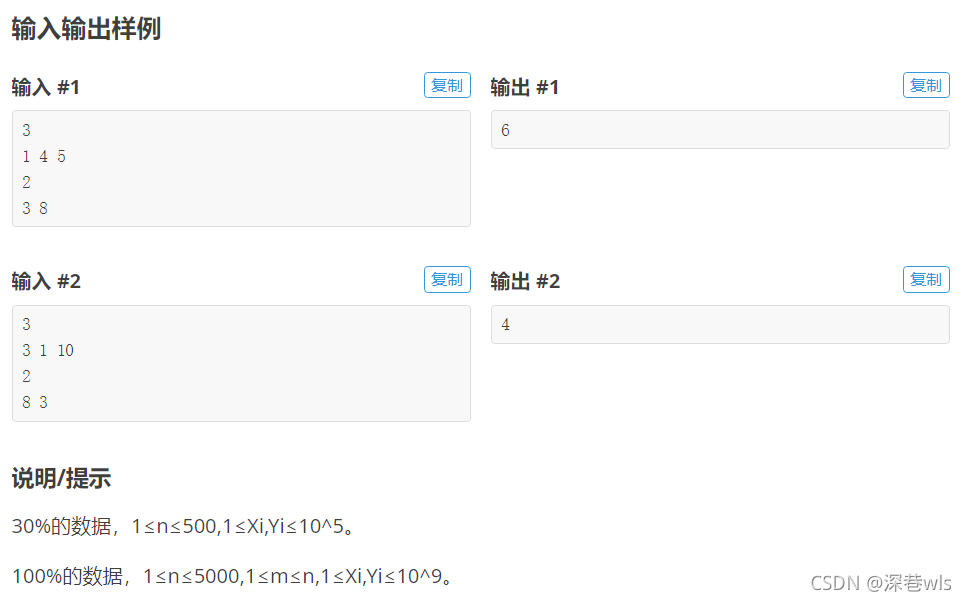
 这篇博客探讨了一道编程题目,即猴子上树问题。通过使用动态规划,作者详细解释了如何用f[i][j]表示前i只猴子上了前j棵树的状态,并给出了C++代码实现。代码中,通过最小化猴子与树之间的距离,找到最优解。最后,程序输出了所有猴子都能上树的最小总距离。
这篇博客探讨了一道编程题目,即猴子上树问题。通过使用动态规划,作者详细解释了如何用f[i][j]表示前i只猴子上了前j棵树的状态,并给出了C++代码实现。代码中,通过最小化猴子与树之间的距离,找到最优解。最后,程序输出了所有猴子都能上树的最小总距离。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








