线性规划算法详解

线性规划

首先什么是线性规划，大致的定义我总结为在线性的目标和约束中，找出一个最优解。

举个例子：

 M1和M2两种原料用于生产内外墙涂料，M1日最大可用量24吨，M2日最大可用量为6吨，外墙涂料每吨需要6吨M1，1吨M2，内墙涂料每吨需要4吨M12，吨M2，外墙涂料每吨利润5个单位，内墙涂料每吨利润4个单位。且市场需求调查数据得出，内墙日需求量不超过外墙的日需求量+1吨，内墙最大日需求量为2吨

怎样在这样的各个线性的条件中，得到最优的内外墙生产吨数，就是我们线性规划算法要做的事情。

设外墙生产x1吨,内墙生产x2吨,设利润为z，要得到z的最大化，也就是最优解，上述条件罗列为公式可得出

1. 6x1+4x2<=24
2. x1+2x2<=6
3. -x1+x2<=1
4. x2<=2
5. x1,x2>0
6. z=5x1+4x2

如何从这个公式中求出最优解？有以下两大方法

图解法

我们将上述约束条件画图，y轴为x2，x轴为x1，得出如下：

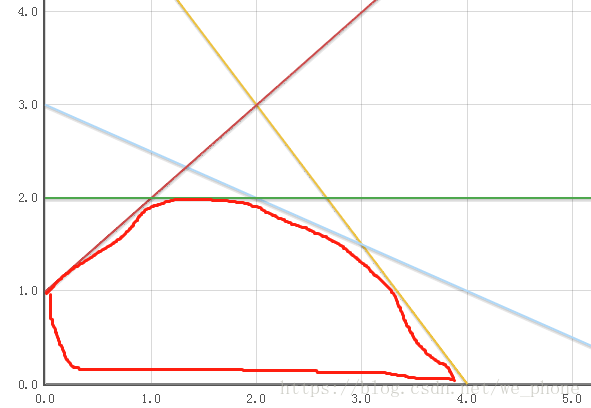
圈红色的部分就是所有的可行解，表示这个区间内都的x1x2能满足约束条件

对于我们的z函数，其实表示的是一条截距为z斜率为-(5/4)的线性直线，我们要求z最大化的最优解，就是在所有的可行区域内找到可以满足z曲线截距最大的点。

最后我们发现，可行区域内能让z函数达到最大截距的点就是我圈出来的那个角点，z再增大的话，就超出可行区域了，所以不满足要求，所以最终得出最优解为x1=3,x2=1.5

这就是图解法的做法，一个定理就是，线性规划的最优解总是发生在约束几何平面的角点上，例如上面圈出来的点，先当做是个定理，我也不知道怎么证明这个定理。

以上就是线性规划的图解法，优点是简单明了，缺点就是当参数超过3个时，我们很难直观画出一个jihe几何平面来找角点，所以我们需要下面的另一种解法。

单纯形法

当超过3个参数时，单纯形法就派上用场了，单纯形法首先要做的就是把方程化为标准形式：

1. 所有的变量都是非负数
2. 所有的约束都是等式(非负限制除外)，且具有非负的右端项

像上述的方程，如果化为标准形式，将会是如下

1. 6x1+4x2+s1=24
2. x1+2x2+s2